कोण: Difference between revisions
No edit summary |
No edit summary |
||
| (5 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
[[File:Positive angle1.jpg|thumb|चित्र-1 धनात्मक कोण]] | |||
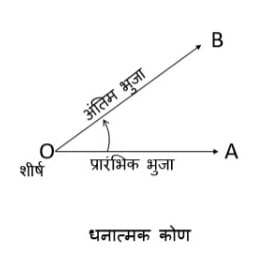
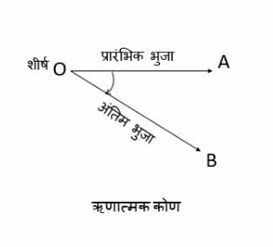
जब दो किरणें एक उभयनिष्ठ बिंदु पर जुड़ती हैं तो एक कोण बनता है। सामान्य बिंदु को नोड या शीर्ष कहा जाता है। कोण किसी दी गई किरण के उसके शीर्ष के चारों ओर घूमने का माप है। मूल किरण को प्रारंभिक पक्ष कहा जाता है और घूर्णन के बाद किरण की अंतिम स्थिति को कोण का अंतिम पक्ष कहा जाता है। घूर्णन बिंदु को शीर्ष कहा जाता है। यदि घूर्णन की दिशा वामावर्त है तो कोण धनात्मक कहा जाता है (चित्र-1), और यदि घूर्णन की दिशा दक्षिणावर्त है तो कोण ऋणात्मक कहा जाता है। (चित्र-2)। किसी कोण का माप प्रारंभिक पक्ष से अंतिम पक्ष प्राप्त करने के लिए किए गए घूर्णन की मात्रा है । | |||
जब दो किरणें एक उभयनिष्ठ बिंदु पर जुड़ती हैं तो एक कोण बनता है। सामान्य बिंदु को नोड या शीर्ष कहा जाता है। कोण किसी दी गई किरण के उसके शीर्ष के चारों ओर घूमने का माप है। मूल किरण को प्रारंभिक पक्ष कहा जाता है और घूर्णन के बाद किरण की अंतिम स्थिति को कोण का अंतिम पक्ष कहा जाता है। घूर्णन बिंदु को शीर्ष कहा जाता है। यदि घूर्णन की दिशा वामावर्त है तो कोण धनात्मक कहा जाता है (चित्र-1), और यदि घूर्णन की दिशा दक्षिणावर्त है तो कोण ऋणात्मक कहा जाता है। (चित्र-2)। किसी कोण का माप प्रारंभिक पक्ष से अंतिम पक्ष प्राप्त करने के लिए किए गए घूर्णन की मात्रा है | [[File:Negative angle1.jpg|thumb|273x273px|चित्र-2 ऋणात्मक कोण]] | ||
== डिग्री माप == | |||
यदि आरंभिक पक्ष से अंतिम पक्ष तक घूर्णन है <math>\left ( \frac{1}{360} \right )</math><sup>वां</sup> कहा जाता है कि एक परिक्रमण के कोण में एक डिग्री का माप 1° लिखा जाता है। | |||
{| class="wikitable" | |||
|+ | |+ | ||
!''1 डिग्री(1°) = 60 मिनट(60')'' | |||
''1 मिनट(1') = 60 सेकंड (60“) '' | |||
|} | |} | ||
== रेडियन माप == | |||
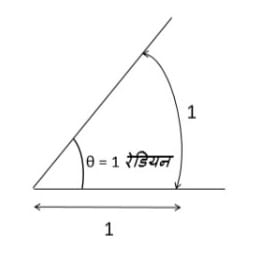
रेडियन कोण मापने की एक अन्य इकाई है। 1 इकाई त्रिज्या वाले वृत्त में 1 इकाई लंबाई के चाप द्वारा केंद्र पर बनाए गए कोण का माप 1 रेडियन कहा जाता है। | रेडियन कोण मापने की एक अन्य इकाई है। 1 इकाई त्रिज्या वाले वृत्त में 1 इकाई लंबाई के चाप द्वारा केंद्र पर बनाए गए कोण का माप 1 रेडियन कहा जाता है। | ||
त्रिज्या | त्रिज्या <math>r</math> के एक वृत्त में, लंबाई का एक चाप <math>l</math> , केंद्र पर एक कोण <math> | ||
\theta</math> रेडियन बनाता है | |||
\theta< | <math>\theta= \frac{l}{r}</math> या <math>l=r\theta</math> | ||
[[File:Radian.jpg|thumb|चित्र 3-रेडियन]] | |||
== डिग्री एवं रेडियन के बीच संबंध == | |||
किसी '''''वृत्त की परिधि''''' <math>=2\pi r</math> | |||
< | यदि किसी '''''वृत्त की त्रिज्या''''' <math>=1</math> है तो '''''वृत्त की परिधि''''' <math>=2\pi</math> होगी. इसलिए प्रारंभिक पक्ष की एक पूर्ण परिक्रमण <math>2\pi</math> का कोण अंतरित करती है और इसकी डिग्री माप <math> | ||
360^\circ</math> होती है । | |||
< | <math>2\pi</math> '''''रेडियन''''' <math>= 360^\circ</math> | ||
<math>\pi</math> '''''रेडियन''''' <math>=180^\circ </math> <math> \pi = \frac{22}{7} </math> | |||
<math>1</math> '''''रेडियन''''' <math>=\frac{180^\circ}{\pi}=\frac{180^\circ \times 7}{22}=57^\circ16' </math> लगभग | |||
<math>\pi </math> '''''रेडियन''''' <math>= 180^\circ </math> अत: <math> 1^\circ =\frac{\pi}{180} </math> '''''रेडियन''''' <math>=\frac{22}{7 \times 180}=0.01746</math> '''''रेडियन''''' लगभग | |||
निम्नलिखित तालिका कुछ सामान्य कोणों की डिग्री माप और रेडियन माप के बीच संबंध को दर्शाती है। | निम्नलिखित तालिका कुछ सामान्य कोणों की डिग्री माप और रेडियन माप के बीच संबंध को दर्शाती है। | ||
{| class="wikitable" | |||
|'''''डिग्री''''' | |||
|<math> 30^\circ </math> | |||
|<math> 45^\circ </math> | |||
|<math> 60^\circ </math> | |||
|<math> 90^\circ </math> | |||
|<math> 180^\circ </math> | |||
|<math> 270^\circ </math> | |||
|<math> 360^\circ </math> | |||
|- | |- | ||
|'''''रेडियन''''' | |||
|<math> \frac{\pi}{6} </math> | |||
|<math> \frac{\pi}{4} </math> | |||
|<math> \frac{\pi}{3} </math> | |||
|<math> \frac{\pi}{2} </math> | |||
|<math> \pi </math> | |||
|<math> \frac{3\pi}{2} </math> | |||
|<math> 2\pi </math> | |||
|} | |} | ||
'''''रेडियन माप''''' <math>=\frac{\pi}{180} \times </math> '''''डिग्री माप''''' | |||
'''''डिग्री''''' '''''माप''''' <math>=\frac{180} {\pi}\times</math> '''''रेडियन माप''''' | |||
=== उदाहरण 1 === | |||
<math>45^\circ 20'</math> को रेडियन माप में परिवर्तित करें। | |||
'''''रेडियन माप''''' <math>=\frac{\pi}{180} \times </math> '''''डिग्री माप''''' | |||
<math>45^\circ 20'=45\frac{1}{3}</math> '''''डिग्री''''' <math>=\frac{136}{3}</math> '''''रेडियन''''' <math>= \frac{\pi}{180} \times \frac{136}{3}=\frac{34\pi}{135} \ </math>'''''रेडियन''''' | |||
< | अत: <math>45^\circ 20'=\frac{34\pi}{135} \ </math>'''''रेडियन''''' | ||
=== उदाहरण 2 === | |||
<math> 4 </math> रेडियन को डिग्री माप में परिवर्तित करें। | |||
'''''डिग्री''''' '''''माप''''' <math>=\frac{180} {\pi}\times</math> '''''रेडियन माप''''' | |||
<math>=\frac{180} {\pi} \times 4 \ </math>'''''डिग्री''''' <math>=\frac{180} {22} \times 7 \times 4 = \frac{2520}{11} =229 \frac{1}{11} \ </math>'''''डिग्री''''' | |||
'''''1 डिग्री (1°) = 60 मिनट (60')''''' | |||
<math>=229 \ </math>'''''डिग्री''''' <math>+ \frac{1 \times 60}{11} \ </math>'''''मिनट''''' | |||
<math> =229 \ </math>'''''डिग्री''''' <math> + 5\frac{5}{11} \ </math>'''''मिनट''''' | |||
'''''1 मिनट(1') = 60 सेकंड (60“)''' '' | |||
<math>=229 \ </math>'''''डिग्री''''' <math> + 5 \ </math>'''''मिनट'''''<math> + \frac{5 \times 60}{11} \ </math>'''''सेकंड''''' | |||
<math>=229 \ </math>'''''डिग्री <math> + 5 \ </math>मिनट'''''<math> + 27.2 \ </math>'''''सेकंड''''' | |||
अत: | अत: <math>4 \ </math>'''''रेडियन'''''<math> =229^\circ 5'27'' </math> लगभग | ||
[[Category: | [[Category:त्रिकोणमितीय फलन]] | ||
[[Category:कक्षा- | [[Category:कक्षा-11]] | ||
[[Category:गणित]] | |||
Latest revision as of 10:23, 27 September 2023
जब दो किरणें एक उभयनिष्ठ बिंदु पर जुड़ती हैं तो एक कोण बनता है। सामान्य बिंदु को नोड या शीर्ष कहा जाता है। कोण किसी दी गई किरण के उसके शीर्ष के चारों ओर घूमने का माप है। मूल किरण को प्रारंभिक पक्ष कहा जाता है और घूर्णन के बाद किरण की अंतिम स्थिति को कोण का अंतिम पक्ष कहा जाता है। घूर्णन बिंदु को शीर्ष कहा जाता है। यदि घूर्णन की दिशा वामावर्त है तो कोण धनात्मक कहा जाता है (चित्र-1), और यदि घूर्णन की दिशा दक्षिणावर्त है तो कोण ऋणात्मक कहा जाता है। (चित्र-2)। किसी कोण का माप प्रारंभिक पक्ष से अंतिम पक्ष प्राप्त करने के लिए किए गए घूर्णन की मात्रा है ।
डिग्री माप
यदि आरंभिक पक्ष से अंतिम पक्ष तक घूर्णन है वां कहा जाता है कि एक परिक्रमण के कोण में एक डिग्री का माप 1° लिखा जाता है।
| 1 डिग्री(1°) = 60 मिनट(60')
1 मिनट(1') = 60 सेकंड (60“) |
|---|
रेडियन माप
रेडियन कोण मापने की एक अन्य इकाई है। 1 इकाई त्रिज्या वाले वृत्त में 1 इकाई लंबाई के चाप द्वारा केंद्र पर बनाए गए कोण का माप 1 रेडियन कहा जाता है।
त्रिज्या के एक वृत्त में, लंबाई का एक चाप , केंद्र पर एक कोण रेडियन बनाता है
या
डिग्री एवं रेडियन के बीच संबंध
किसी वृत्त की परिधि
यदि किसी वृत्त की त्रिज्या है तो वृत्त की परिधि होगी. इसलिए प्रारंभिक पक्ष की एक पूर्ण परिक्रमण का कोण अंतरित करती है और इसकी डिग्री माप होती है ।
रेडियन
रेडियन
रेडियन लगभग
रेडियन अत: रेडियन रेडियन लगभग
निम्नलिखित तालिका कुछ सामान्य कोणों की डिग्री माप और रेडियन माप के बीच संबंध को दर्शाती है।
| डिग्री | |||||||
| रेडियन |
रेडियन माप डिग्री माप
डिग्री माप रेडियन माप
उदाहरण 1
को रेडियन माप में परिवर्तित करें।
रेडियन माप डिग्री माप
डिग्री रेडियन रेडियन
अत: रेडियन
उदाहरण 2
रेडियन को डिग्री माप में परिवर्तित करें।
डिग्री माप रेडियन माप
डिग्री डिग्री
1 डिग्री (1°) = 60 मिनट (60')
डिग्री मिनट
डिग्री मिनट
1 मिनट(1') = 60 सेकंड (60“)
डिग्री मिनटसेकंड
डिग्री मिनटसेकंड
अत: रेडियन लगभग