द्विघात समीकरण: Difference between revisions
No edit summary |
No edit summary |
||
| Line 2: | Line 2: | ||
[[Category:द्विघात समीकरण]] | [[Category:द्विघात समीकरण]] | ||
[[Category:गणित]][[Category:कक्षा-10]] | [[Category:गणित]][[Category:कक्षा-10]] | ||
ऐसा समीकरण, जिन्हें हम <math>ax^2+bx+c=0</math> रूप में निरूपित कर सकते हैं , जहां <math>a,b,c</math> वास्तविक संख्याएं हैं | ऐसा समीकरण, जिन्हें हम <math>ax^2+bx+c=0</math> रूप में निरूपित कर सकते हैं , जहां <math>a,b,c</math> वास्तविक संख्याएं हैं एवं <math>a\neq0</math> , उन्हें हम द्विघात समीकरण कहते हैं। सरल शब्दों में हम कह सकते हैं कि , <math>p(x)=0</math> के रूप का कोई भी समीकरण, जहाँ <math>p(x)</math> द्विघात वाला एक बहुपद है , द्विघात समीकरण कहलाता है । | ||
== द्विघात समीकरण का मानक रूप == | == द्विघात समीकरण का मानक रूप == | ||
जब हम <math>p(x)</math> ( एक द्विघात बहुपद) के सभी पदों को उनके घात के अनुसार अवरोही क्रम में लिखते हैं , तो यह द्विघात समीकरण का मानक रूप कहलाता है । | जब हम <math>p(x)</math> (एक द्विघात बहुपद) के सभी पदों को उनके घात के अनुसार अवरोही क्रम में लिखते हैं, तो यह द्विघात समीकरण का मानक रूप कहलाता है । | ||
मानक रूप : <math>ax^2+bx+c=0</math><ref>{{Cite book |title=MATHEMATICS (NCERT) |edition=Revised |pages=38-41}}</ref> , <math>a\neq0</math> [ <math>a,b,c</math> वास्तविक संख्याएं हैं ] | मानक रूप : <math>ax^2+bx+c=0</math><ref>{{Cite book |title=MATHEMATICS (NCERT) |edition=Revised |pages=38-41}}</ref> , <math>a\neq0</math> [ <math>a,b,c</math> वास्तविक संख्याएं हैं ] | ||
| Line 18: | Line 18: | ||
=== उदाहरण 2 === | === उदाहरण 2 === | ||
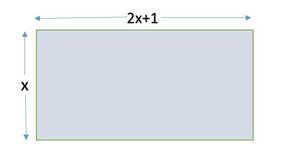
एक आयत का क्षेत्रफल <math>545</math> है। आयत की लंबाई चौड़ाई के दोगुने से एक अधिक है । इस कथन को द्विघात समीकरण रूप में निरूपित करें । | एक आयत का क्षेत्रफल <math>545</math> है। आयत की लंबाई, चौड़ाई के दोगुने से एक अधिक है । इस कथन को द्विघात समीकरण रूप में निरूपित करें । | ||
[[File:आयत.jpg|thumb|282x282px|आयत]] | [[File:आयत.jpg|thumb|282x282px|आयत]] | ||
हल | हल | ||
| Line 71: | Line 71: | ||
<math>x^2-6x+8=0</math> | <math>x^2-6x+8=0</math> | ||
उपर्युक्त समीकरण | उपर्युक्त समीकरण द्विघात समीकरण का मानक रूप <math>ax^2+bx+c=0</math> प्रदर्शित करता है , अतः यह एक द्विघात समीकरण है । | ||
2) <math>x(4x+8)=x^2+4</math> | 2) <math>x(4x+8)=x^2+4</math> | ||
| Line 85: | Line 85: | ||
<math>3x^2+8x-4=0</math> | <math>3x^2+8x-4=0</math> | ||
उपर्युक्त समीकरण | उपर्युक्त समीकरण द्विघात समीकरण का मानक रूप <math>ax^2+bx+c=0</math> प्रदर्शित करता है , अतः यह एक द्विघात समीकरण है । | ||
3) <math>(x+2)^3=x^3-6</math> | 3) <math>(x+2)^3=x^3-6</math> | ||
| Line 124: | Line 124: | ||
# दो क्रमागत धनात्मक पूर्णांकों का गुणनफल <math>400</math> है। इस कथन को द्विघात समीकरण रूप में निरूपित करें । | # दो क्रमागत धनात्मक पूर्णांकों का गुणनफल <math>400</math> है। इस कथन को द्विघात समीकरण रूप में निरूपित करें । | ||
# रोहन की माँ उससे <math>40</math> वर्ष बड़ी है। उनकी आयु का गुणनफल (वर्षों में) अब से <math>4</math> वर्ष बाद <math>410</math> | # रोहन की माँ उससे <math>40</math> वर्ष बड़ी है। उनकी आयु का गुणनफल (वर्षों में) अब से <math>4</math> वर्ष बाद <math>410</math> होगा। इस कथन को द्विघात समीकरण रूप में निरूपित करें । | ||
== संदर्भ == | == संदर्भ == | ||
Revision as of 15:20, 29 September 2023
ऐसा समीकरण, जिन्हें हम रूप में निरूपित कर सकते हैं , जहां वास्तविक संख्याएं हैं एवं , उन्हें हम द्विघात समीकरण कहते हैं। सरल शब्दों में हम कह सकते हैं कि , के रूप का कोई भी समीकरण, जहाँ द्विघात वाला एक बहुपद है , द्विघात समीकरण कहलाता है ।
द्विघात समीकरण का मानक रूप
जब हम (एक द्विघात बहुपद) के सभी पदों को उनके घात के अनुसार अवरोही क्रम में लिखते हैं, तो यह द्विघात समीकरण का मानक रूप कहलाता है ।
मानक रूप : [1] , [ वास्तविक संख्याएं हैं ]
उदाहरण 1
द्विघात समीकरण के कुछ उदाहरण निम्नलिखित हैं :
उदाहरण 2
एक आयत का क्षेत्रफल है। आयत की लंबाई, चौड़ाई के दोगुने से एक अधिक है । इस कथन को द्विघात समीकरण रूप में निरूपित करें ।
हल
मान लीजिए , आयत की चौड़ाई
उपर्युक्त कथन के अनुसार ,
आयत की लंबाई
आयत का क्षेत्रफल
हम जानते हैं कि , आयत का क्षेत्रफल = लंबाई चौड़ाई
मान रखने पर ,
अतः , उपर्युक्त कथन का द्विघात समीकरण है ।
उदाहरण 3
स्पष्ट करें कि क्या निम्नलिखित समीकरण द्विघात समीकरण हैं ?
1)
2)
3)
4)
हल
1)
उपर्युक्त समीकरण का विस्तृत रूप लिखने पर,
सूत्र:
सभी पदों को दाएं पक्ष में स्थानांतरित करने पर ,
उपर्युक्त समीकरण द्विघात समीकरण का मानक रूप प्रदर्शित करता है , अतः यह एक द्विघात समीकरण है ।
2)
उपर्युक्त समीकरण का विस्तृत रूप लिखने पर ,
सभी पदों को दाएं पक्ष में स्थानांतरित करने पर ,
उपर्युक्त समीकरण द्विघात समीकरण का मानक रूप प्रदर्शित करता है , अतः यह एक द्विघात समीकरण है ।
3)
उपर्युक्त समीकरण का विस्तृत रूप लिखने पर ,
सूत्र :
सभी पदों को दाएं पक्ष में स्थानांतरित करने पर ,
उपर्युक्त समीकरण द्विघात समीकरण का मानक रूप प्रदर्शित करता है , अतः यह एक द्विघात समीकरण है ।
4)
उपर्युक्त समीकरण का विस्तृत रूप लिखने पर ,
सभी पदों को दाएं पक्ष में स्थानांतरित करने पर ,
उपर्युक्त समीकरण द्विघात समीकरण का मानक रूप नही प्रदर्शित करता है , अतः यह एक द्विघात समीकरण नही है ।
अभ्यास प्रश्न
- दो क्रमागत धनात्मक पूर्णांकों का गुणनफल है। इस कथन को द्विघात समीकरण रूप में निरूपित करें ।
- रोहन की माँ उससे वर्ष बड़ी है। उनकी आयु का गुणनफल (वर्षों में) अब से वर्ष बाद होगा। इस कथन को द्विघात समीकरण रूप में निरूपित करें ।
संदर्भ
- ↑ MATHEMATICS (NCERT) (Revised ed.). pp. 38–41.