वेन आरेख: Difference between revisions
(content modified) |
(image added) |
||
| (3 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
वेन आरेख एक आरेख है जो हमें समुच्चय/सेट और उनके अवयवों के बीच तार्किक संबंध को देखने में मदद करता है और इन समुच्चयों के आधार पर उदाहरणों को हल करने में हमारी सहायता करता है। | |||
वेन आरेख एक आरेख है जो हमें समुच्चय/सेट और उनके | |||
== वेन आरेख से संबंधित पद == | == वेन आरेख से संबंधित पद == | ||
[[File:Universal Set.jpg|thumb|चित्र-1 सार्वत्रिक समुच्चय]] | |||
=== सार्वत्रिक समुच्चय === | === सार्वत्रिक समुच्चय === | ||
जब भी हम किसी समुच्चय का उपयोग करते हैं, तो पहले एक बड़े समुच्चय पर विचार करना आसान होता है जिसे सार्वत्रिक समुच्चय कहा जाता है जिसमें उन सभी समुच्चयों के सभी | जब भी हम किसी समुच्चय का उपयोग करते हैं, तो पहले एक बड़े समुच्चय पर विचार करना आसान होता है जिसे सार्वत्रिक समुच्चय कहा जाता है जिसमें उन सभी समुच्चयों के सभी अवयव सम्मिलित होते हैं जिन पर विचार किया जा रहा है। | ||
जब भी हम कोई वेन आरेख बनाते हैं: | जब भी हम कोई वेन आरेख बनाते हैं: | ||
| Line 19: | Line 18: | ||
* <math>1-12</math> के बीच की सभी संख्याएँ, जो सम नहीं हैं, वृत्त के बाहर और आयत के भीतर रखी जाएँगी जैसा कि ऊपर दिखाया गया है। | * <math>1-12</math> के बीच की सभी संख्याएँ, जो सम नहीं हैं, वृत्त के बाहर और आयत के भीतर रखी जाएँगी जैसा कि ऊपर दिखाया गया है। | ||
* <math>U=\{1,2,3,......,12\}</math> एक सार्वत्रिक समुच्चय है जिसका <math>A=\{2,4,6,8,10,12\}</math> एक उपसमुच्चय है। | * <math>U=\{1,2,3,......,12\}</math> एक सार्वत्रिक समुच्चय है जिसका <math>A=\{2,4,6,8,10,12\}</math> एक उपसमुच्चय है। | ||
[[File:Sub Set.jpg|thumb|चित्र-2 उपसमुच्चय]] | |||
=== उप समुच्चय === | |||
उपसमुच्चय वह समुच्चय है जो किसी अन्य समुच्चय में अंतर्विष्ट होता है। चित्र 2 में हमारे पास दो समुच्चय A और B हैं। <math>A=\{2,4,6,8,10,12\}</math> और <math>B=\{4,6,8\}</math> | |||
यहां, B, A का एक उपसमुच्चय है जिसे <math>B\subset A</math> द्वारा दर्शाया गया है। वृत B, वृत A के भीतर अंतर्विष्ट है। साथ ही, B के सभी अवयव समुच्चय A के अवयव हैं। ये सभी समुच्चय A और B सार्वत्रिक समुच्चय <math>U=\{1,2,3,......,12\}</math> के भीतर अंतर्विष्ट हैं। | |||
[[Category:समुच्चय]][[Category:कक्षा-11]][[Category:गणित]] | [[Category:समुच्चय]][[Category:कक्षा-11]][[Category:गणित]] | ||
Latest revision as of 17:43, 30 November 2023
वेन आरेख एक आरेख है जो हमें समुच्चय/सेट और उनके अवयवों के बीच तार्किक संबंध को देखने में मदद करता है और इन समुच्चयों के आधार पर उदाहरणों को हल करने में हमारी सहायता करता है।
वेन आरेख से संबंधित पद
सार्वत्रिक समुच्चय
जब भी हम किसी समुच्चय का उपयोग करते हैं, तो पहले एक बड़े समुच्चय पर विचार करना आसान होता है जिसे सार्वत्रिक समुच्चय कहा जाता है जिसमें उन सभी समुच्चयों के सभी अवयव सम्मिलित होते हैं जिन पर विचार किया जा रहा है।
जब भी हम कोई वेन आरेख बनाते हैं:
- सार्वत्रिक समुच्चय को प्रदर्शित करने के लिए एक बड़े आयत का उपयोग किया जाता है और इसे प्रायः प्रतीक द्वारा दर्शाया जाता है।
- अन्य सभी समुच्चय इस बड़े आयत के भीतर वृत्तों या बंद आकृतियों द्वारा दर्शाए गए हैं।
- प्रत्येक समुच्चय सार्वत्रिक समुच्चय का उपसमुच्चय है।
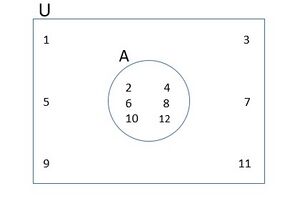
चित्र-1 पर विचार करें। यहाँ
- , आयत के भीतर संलग्न सभी संख्याओं वाला सार्वभौमिक समुच्चय है।
- , सम संख्याओं का समुच्चय है, जिसे एक वृत्त में रखा गया है जो सार्वत्रिक समुच्चय का उपसमुच्चय है और इसे आयत के अंदर रखा गया है।
- के बीच की सभी संख्याएँ, जो सम नहीं हैं, वृत्त के बाहर और आयत के भीतर रखी जाएँगी जैसा कि ऊपर दिखाया गया है।
- एक सार्वत्रिक समुच्चय है जिसका एक उपसमुच्चय है।
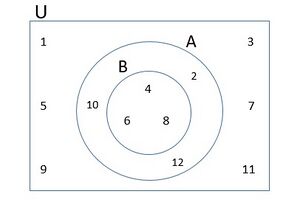
उप समुच्चय
उपसमुच्चय वह समुच्चय है जो किसी अन्य समुच्चय में अंतर्विष्ट होता है। चित्र 2 में हमारे पास दो समुच्चय A और B हैं। और
यहां, B, A का एक उपसमुच्चय है जिसे द्वारा दर्शाया गया है। वृत B, वृत A के भीतर अंतर्विष्ट है। साथ ही, B के सभी अवयव समुच्चय A के अवयव हैं। ये सभी समुच्चय A और B सार्वत्रिक समुच्चय के भीतर अंतर्विष्ट हैं।