आकुंचन

Buckling

भौतिकी में ,आकुंचन (बकलिंग) एक ऐसी घटना है जो तब होती है जब एक पतली संरचना, जैसे कि स्तंभ या बीम, संपीड़न भार के अधीन अपना आकार खो देता है,इस प्रकार, ऐसे स्तंभ (बीम या दंड) स्वयं की निर्धारित व अभिकल्पित क्रिया कलाप करने में समर्थ नहीं रहते व विफल माने जाते हैं । ऐसा तब होता है,जब इन स्तंभों अथवा इन स्थभों से निर्मित अधोरचना पर आरोपित बल, एक महत्वपूर्ण मान (जिसकी अधोरचना पूर्व गणना मान्य है ) से अधिक हो जाता है । ऐसा होने पर,इन स्तंभों अथवा इन स्थभों से निर्मित संरचना, तन्य रूप से विकृत ,न होकर अचानक झुक जाती है या झुकने लगती है। इसे स्तंभों अथवा इन स्थभों से निर्मित संरचना, की विफलता माना जाता है ।

समझने के लिए:एक सरल उदाहरण

अक्ष-केंद्रित भार के अधीन ,आकुंचन की विशेष विकृति प्रदर्शित करने वाले एक स्तंभ का आरेख

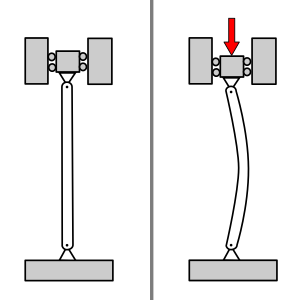
एक वृहद ,पतला ,स्तंभ अपनी लंबवत अवस्था में ,शीर्ष पर एक भार का समर्थन करता है। एक संपीड़न बल लगने के अवस्था में यह स्तंभ,लघु रूप धारणा करने की चेष्टा के अधीन हो जाता है व इसकी संरणचना विकृत होने का प्रयास करने लगता है। प्रारंभ में, स्तंभ प्रत्यास्थ रूप से विकृत हो जाएगा, जिसका अर्थ है कि यह भार के अधीन लघु मात्र में आकुंचित हो ने लगेगा (झुक जाएगा) परंतु बल के हट जाने, पर यह अपने मूल आकार में वापस आ जाएगा।

संपीड़न बल में बढ़ोतरी

संपीड़न बल की बढ़ोतरी की अवधि में , एक समय ऐसा आता है, जब स्तंभ पर आरोपित बल ,उसकी संरचना की भार झेलने की क्षमता से अधिक हो जाता है। इस भार का मूल्य महत्वपूर्ण है,क्योंकि इसस भार पर स्तंभ अस्थिरता का अनुभव करता है । ऐसी स्थिती में वह न केवल झुकने लगता है बल्कि अचानक पार्श्व भाग की ओर झुकने लगता है।

तनाव के दो मुख्य प्रकार

यह (अचानक झुकने वाला) व्यवहार संपीड़न बल और पदार्थ की कठोरता के बीच परस्पर क्रिया के कारण होता है। इसस प्रकार ,जब एक विरल व क्षीण (पतली) संरचना को संपीड़ित किया जाता है, तो यह दो मुख्य प्रकार के तनाव का अनुभव करता है:

संपीड़न तनाव (धकेलने वाला बल)

और

झुकने वाला तनाव (पार्श्व अवस्थित बल)

संपीड़न तनाव संरचना को लघु कर देता (छोटा) है, जबकि झुकने वाला तनाव इसे मोड़ने या झुकने का प्रयास करता है।

भार के जिस महत्वपूर्ण मूल्य पर आकुंचन की स्थिती बन जाती है, वह इस घटना क्रम के लीये उतरदायी कई कारकों पर निर्भर करता है। संरचना की लंबाई और क्रॉस-अनुभागीय गुण महत्वपूर्ण भूमिका निभाते हैं। लघु स्तंभों की अपेक्षा बृहद् स्तंभों में झुकाव की संभावना अधिक होती है क्योंकि उनके पार्श्व में विक्षेपित होने की प्रवृत्ति अधिक होती है। इसके अतिरिक्त, स्तंभ का आकार और भौतिक गुण भी इसके झुकने के व्यवहार को प्रभावित करते हैं।

आदर्श स्तंभ के परिकल्पित गुण

यहाँ ये ज्ञात रहना महत्वपूर्ण है की,एक आकुंचित अवस्था की गणना करते समय एक आदर्श स्तंभ को परिकल्पित कीया जाता है जिसमें निम्न प्रकार के भौतिक गुण पाए जाते हैं :

•    स्तंभ पूर्णत: सटीक है
•    स्तंभ सजातीय पददार्थों (सामग्री) से बना है
•    स्तंभ अपनी आरंभिक स्थिती में किसी भी प्रकार के तनाव से मुक्त है

जब आरोपित भार, उस महत्वपूर्ण मूल्य पर पहुँच जाता है,तब स्तंभ अस्थिर संतुलन की स्थिति में रहता है । उस भार पर, थोड़े से पार्श्व बल के आरोपित होने से स्तंभ एक नए विन्यास में अचानक "बदलने " से विफल हो जाएगा, और कहा जाता है कि स्तंभ झुक गया है।

गणितीय रूप से

आकुंचन सूत्र का उपयोग करके, आकुंचन का विश्लेषण किया जा सकता है, जो एक आदर्श स्तम्भ, पूरी तरह से सीधे कॉलम के लिए महत्वपूर्ण भार का अनुमान देता है। सूत्र महत्वपूर्ण भार को स्तंभ की लंबाई, भौतिक गुणों और जड़त्व-आघूर्ण (स्तंभ के झुकने के प्रतिरोध का एक माप) से संबंधित करता है।

$F_{c}={\frac {\pi ^{2}EI}{(KL)^{2}}}$