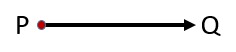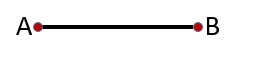रेखाएँ और कोण - परिभाषाएँ: Difference between revisions
(New Mathematics Class 9 Hindi Page Created) |
(added content) |
||
| (5 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
[[Category:रेखाएँ और कोण]][[Category:कक्षा-9]][[Category:गणित]] | [[Category:रेखाएँ और कोण]][[Category:कक्षा-9]][[Category:गणित]] | ||
ज्यामिति में, रेखाएँ और कोण मूल शब्द हैं जो विषय की नींव | ज्यामिति में, रेखाएँ और कोण मूल शब्द हैं जो विषय की नींव स्थापित करते हैं। एक रेखा को निकट दूरी पर स्थित बिंदुओं की एक पंक्ति के रूप में परिभाषित किया जाता है जो दो दिशाओं में असीमित रूप से फैली होती है। इसका केवल एक ही आयाम है, वह है इसकी लंबाई। कागज के एक टुकड़े पर खींचा गया एक क्षैतिज चिह्न एक रेखा का उदाहरण माना जा सकता है। कोण को दो किरणों द्वारा निर्मित एक आकृति के रूप में परिभाषित किया जाता है जो एक सामान्य समापन बिंदु पर मिलती हैं। इन्हें एक चांदे(प्रोट्रैक्टर) का उपयोग करके डिग्री में मापा जाता है। सभी ज्यामितीय आकृतियों में रेखाएँ और कोण होते हैं। | ||
== रेखा == | |||
रेखा एक आयामी आकृति है जो बिना किसी चौड़ाई के दोनों दिशाओं में असीमित रूप से फैली हुई है। यह एक दूसरे के निकट अनंत संख्या में बिंदुओं से बना है। चित्र-1 देखें[[File:Line - one Dimension in Onshape.png|alt=Fig.1 Line|none|thumb|200x200px|चित्र-1 रेखा]] | |||
== किरण == | |||
किरणें वे रेखाएँ हैं जिनका एक छोर आरंभ बिंदु है और दूसरा छोर अनंत तक जाता है। वे बिना समाप्त हुए एक दिशा में विस्तारित होती हैं। चित्र-2 देखें। | |||
जब दो किरणें एक दूसरे से जुड़ती हैं, तो वे एक कोण बनाती हैं।[[File:Ray - Line.jpg|alt=Fig.2 Ray|none|thumb|चित्र-2 किरण]] | |||
== रेखाखण्ड == | |||
जब किसी रेखा के दो अंतिम बिंदु होते हैं, तो उसे रेखाखंड के रूप में जाना जाता है। चित्र-3 देखें। | |||
[[File:Line segment.jpg|alt=Fig.3 Line Segment|none|thumb|चित्र-3 रेखाखण्ड]] | |||
== संरेख बिन्दु == | |||
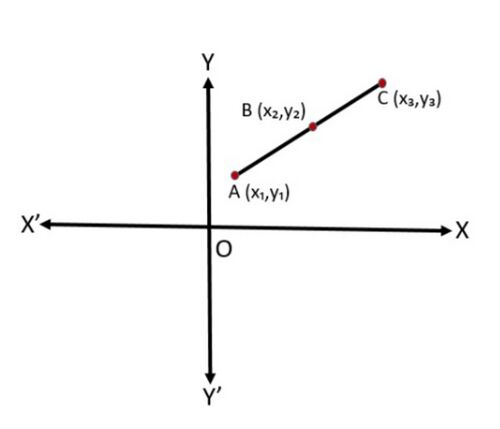
संरेख बिंदु तीन या उससे अधिक बिंदुओं का समूह है जो एक ही सीधी रेखा पर स्थित होते हैं। कोई भी तीन या उससे अधिक बिंदु केवल तभी संरेख होंगे जब वे एक ही सीधी रेखा में हों। चित्र-4 में देखें कि बिंदु A, B और C संरेख बिंदु हैं। | |||
[[File:Collinear Points.jpg|alt=Fig. 4 Collinear Points|none|thumb|500x500px|चित्र-4 संरेख बिन्दु]] | |||
== असंरेख बिन्दु == | |||
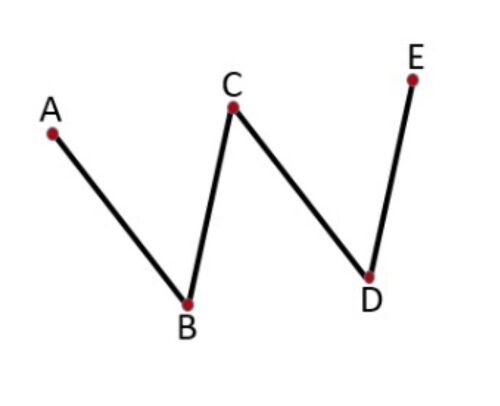
यदि तीन या उससे अधिक बिंदु एक ही सीधी रेखा पर स्थित नहीं हैं, तो उन्हें असंरेख बिंदु कहा जाता है। नीचे दिए गए चित्र-5 में, बिंदु A, B, C, D और E असंरेख बिंदु हैं क्योंकि वे एक ही सीधी रेखा पर स्थित नहीं हैं।[[File:Non-Collinear Points.jpg|alt=Fig. 5 Non-Collinear Points|none|thumb|500x500px|चित्र-5 असंरेख बिन्दु]] | |||
Latest revision as of 15:48, 6 June 2024
ज्यामिति में, रेखाएँ और कोण मूल शब्द हैं जो विषय की नींव स्थापित करते हैं। एक रेखा को निकट दूरी पर स्थित बिंदुओं की एक पंक्ति के रूप में परिभाषित किया जाता है जो दो दिशाओं में असीमित रूप से फैली होती है। इसका केवल एक ही आयाम है, वह है इसकी लंबाई। कागज के एक टुकड़े पर खींचा गया एक क्षैतिज चिह्न एक रेखा का उदाहरण माना जा सकता है। कोण को दो किरणों द्वारा निर्मित एक आकृति के रूप में परिभाषित किया जाता है जो एक सामान्य समापन बिंदु पर मिलती हैं। इन्हें एक चांदे(प्रोट्रैक्टर) का उपयोग करके डिग्री में मापा जाता है। सभी ज्यामितीय आकृतियों में रेखाएँ और कोण होते हैं।
रेखा
रेखा एक आयामी आकृति है जो बिना किसी चौड़ाई के दोनों दिशाओं में असीमित रूप से फैली हुई है। यह एक दूसरे के निकट अनंत संख्या में बिंदुओं से बना है। चित्र-1 देखें
किरण
किरणें वे रेखाएँ हैं जिनका एक छोर आरंभ बिंदु है और दूसरा छोर अनंत तक जाता है। वे बिना समाप्त हुए एक दिशा में विस्तारित होती हैं। चित्र-2 देखें।
जब दो किरणें एक दूसरे से जुड़ती हैं, तो वे एक कोण बनाती हैं।
रेखाखण्ड
जब किसी रेखा के दो अंतिम बिंदु होते हैं, तो उसे रेखाखंड के रूप में जाना जाता है। चित्र-3 देखें।
संरेख बिन्दु
संरेख बिंदु तीन या उससे अधिक बिंदुओं का समूह है जो एक ही सीधी रेखा पर स्थित होते हैं। कोई भी तीन या उससे अधिक बिंदु केवल तभी संरेख होंगे जब वे एक ही सीधी रेखा में हों। चित्र-4 में देखें कि बिंदु A, B और C संरेख बिंदु हैं।
असंरेख बिन्दु
यदि तीन या उससे अधिक बिंदु एक ही सीधी रेखा पर स्थित नहीं हैं, तो उन्हें असंरेख बिंदु कहा जाता है। नीचे दिए गए चित्र-5 में, बिंदु A, B, C, D और E असंरेख बिंदु हैं क्योंकि वे एक ही सीधी रेखा पर स्थित नहीं हैं।