मध्य-बिंदु प्रमेय: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
One of the important theorems in the field of geometry that deals with the properties of triangles are called the '''Mid-Point Theorem.''' | |||
The theory of midpoint theorem is used in coordinate geometry, stating that the midpoint of the line segment is an average of the endpoints. The ‘x’ and the ‘y’ coordinates must be known for solving an equation using this theorem. The Mid-Point Theorem is also useful in the fields of calculus and algebra. | |||
== Mid-Point Theorem Statement == | |||
The midpoint theorem states that “The line segment in a triangle joining the midpoint of any two sides of the triangle is said to be parallel to its third side and is also half of the length of the third side.” | |||
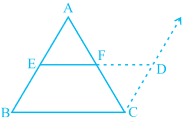
[[File:Midpoint theorem.jpg|alt=Fig. 1|thumb|Fig. 1]] | |||
In the triangle shown in Fig. 1 <math>E</math> and <math>F</math> are midpoint of two sides of the triangle | |||
<math>EF \parallel BC</math> ,<math>EF=\frac{1}{2}BC</math> and <math>\angle AEF=\angle ABC</math> | |||
with this we arrive at the following theorems | |||
'''Theorem 1:'''The line segment joining the mid-points of two sides of a triangle | |||
is parallel to the third side. | |||
'''Theorem 2:'''The line drawn through the mid-point of one side of a triangle, | |||
parallel to another side bisects the third side. | |||
[[Category:चतुर्भुज]][[Category:कक्षा-9]][[Category:गणित]] | [[Category:चतुर्भुज]][[Category:कक्षा-9]][[Category:गणित]] | ||
Revision as of 10:20, 9 September 2024
One of the important theorems in the field of geometry that deals with the properties of triangles are called the Mid-Point Theorem.
The theory of midpoint theorem is used in coordinate geometry, stating that the midpoint of the line segment is an average of the endpoints. The ‘x’ and the ‘y’ coordinates must be known for solving an equation using this theorem. The Mid-Point Theorem is also useful in the fields of calculus and algebra.
Mid-Point Theorem Statement
The midpoint theorem states that “The line segment in a triangle joining the midpoint of any two sides of the triangle is said to be parallel to its third side and is also half of the length of the third side.”
In the triangle shown in Fig. 1 and are midpoint of two sides of the triangle
, and
with this we arrive at the following theorems
Theorem 1:The line segment joining the mid-points of two sides of a triangle
is parallel to the third side.
Theorem 2:The line drawn through the mid-point of one side of a triangle,
parallel to another side bisects the third side.