मध्य-बिंदु प्रमेय: Difference between revisions

Revision as of 11:12, 9 September 2024

ज्यामिति के क्षेत्र में त्रिभुजों के गुणों से संबंधित महत्वपूर्ण प्रमेयों में से एक को मध्य-बिंदु प्रमेय कहा जाता है।

मध्य-बिंदु प्रमेय के सिद्धांत का उपयोग निर्देशांक ज्यामिति में किया जाता है, जिसमें कहा गया है कि रेखाखंड का मध्यबिंदु अंत बिंदुओं का औसत होता है। इस प्रमेय का उपयोग करके समीकरण को हल करने के लिए 'x' और 'y' निर्देशांक ज्ञात होना चाहिए। मध्य-बिंदु प्रमेय कलन और बीजगणित के क्षेत्र में भी उपयोगी है।

मध्य-बिंदु प्रमेय कथन

मध्यबिंदु प्रमेय कहता है कि "किसी त्रिभुज में उसकी किन्हीं दो भुजाओं के मध्यबिंदु को मिलाने वाला रेखाखंड उसकी तीसरी भुजा के समांतर कहलाता है और तीसरी भुजा की लंबाई का आधा भी होता है।"

चित्र-1

चित्र-1 में दर्शाए गए त्रिभुज में $E$ और $F$ त्रिभुज की दो भुजाओं के मध्यबिंदु हैं

$EF\parallel BC$ , $EF={\frac {1}{2}}BC$ and $\angle AEF=\angle ABC$

इसके साथ, हम निम्नलिखित प्रमेयों पर पहुँचते हैं

प्रमेय 1: त्रिभुज की दो भुजाओं के मध्य-बिंदुओं को मिलाने वाला रेखाखंड तीसरी भुजा के समांतर होता है।

प्रमेय 2: त्रिभुज की एक भुजा के मध्य-बिंदु से होकर दूसरी भुजा के समांतर खींची गई रेखा तीसरी भुजा को समद्विभाजित करती है।

@@ Line 1: / Line 1: @@
-One of the important theorems in the field of geometry that deals with the properties of triangles are called the '''Mid-Point Theorem.'''
+ज्यामिति के क्षेत्र में त्रिभुजों के गुणों से संबंधित महत्वपूर्ण प्रमेयों में से एक को मध्य-बिंदु प्रमेय कहा जाता है।
-The theory of midpoint theorem is used in coordinate geometry, stating that the midpoint of the line segment is an average of the endpoints. The ‘x’ and the ‘y’ coordinates must be known for solving an equation using this theorem. The Mid-Point Theorem is also useful in the fields of calculus and algebra.
+मध्य-बिंदु प्रमेय के सिद्धांत का उपयोग निर्देशांक ज्यामिति में किया जाता है, जिसमें कहा गया है कि रेखाखंड का मध्यबिंदु अंत बिंदुओं का औसत होता है। इस प्रमेय का उपयोग करके समीकरण को हल करने के लिए 'x' और 'y' निर्देशांक ज्ञात होना चाहिए। मध्य-बिंदु प्रमेय कलन और बीजगणित के क्षेत्र में भी उपयोगी है।
-== Mid-Point Theorem Statement ==
+== मध्य-बिंदु प्रमेय कथन ==
-The midpoint theorem states that “The line segment in a triangle joining the midpoint of any two sides of the triangle is said to be parallel to its third side and is also half of the length of the third side.”
+मध्यबिंदु प्रमेय कहता है कि "किसी त्रिभुज में उसकी किन्हीं दो भुजाओं के मध्यबिंदु को मिलाने वाला रेखाखंड उसकी तीसरी भुजा के समांतर कहलाता है और तीसरी भुजा की लंबाई का आधा भी होता है।"
-[[File:Midpoint theorem.jpg|alt=Fig. 1|thumb|Fig. 1]]
+[[File:Midpoint theorem.jpg|alt=Fig. 1|thumb|चित्र-1]]
-In the  triangle shown in Fig. 1 <math>E</math> and <math>F</math> are midpoint of two sides of the triangle
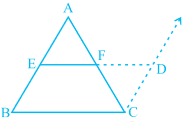
+चित्र-1 में दर्शाए गए त्रिभुज में <math>E</math> और <math>F</math> त्रिभुज की दो भुजाओं के मध्यबिंदु हैं
 <math>EF \parallel BC</math> ,<math>EF=\frac{1}{2}BC</math> and <math>\angle AEF=\angle ABC</math>
-with this we arrive at the following theorems
+इसके साथ, हम निम्नलिखित प्रमेयों पर पहुँचते हैं
-'''Theorem 1:'''The line segment joining the mid-points of two sides of a triangle
+'''प्रमेय 1''': त्रिभुज की दो भुजाओं के मध्य-बिंदुओं को मिलाने वाला रेखाखंड तीसरी भुजा के समांतर होता है।
-is parallel to the third side.
+'''प्रमेय 2''': त्रिभुज की एक भुजा के मध्य-बिंदु से होकर दूसरी भुजा के समांतर खींची गई रेखा तीसरी भुजा को समद्विभाजित करती है।
-'''Theorem 2:'''The line drawn through the mid-point of one side of a triangle,
-parallel to another side bisects the third side.
 [[Category:चतुर्भुज]][[Category:कक्षा-9]][[Category:गणित]]