सम्मिश्र तल: Difference between revisions
(added content) |
(image added) |
||
| Line 48: | Line 48: | ||
आइए वास्तविक संख्या रेखा को हमेशा की तरह बाएँ-दाएँ घुमाएँ और काल्पनिक संख्या रेखा को ऊपर-नीचे करें: | आइए वास्तविक संख्या रेखा को हमेशा की तरह बाएँ-दाएँ घुमाएँ और काल्पनिक संख्या रेखा को ऊपर-नीचे करें: | ||
[[File:सम्मिश्र संख्या.jpg|thumb|चित्र-सम्मिश्र संख्या]] | |||
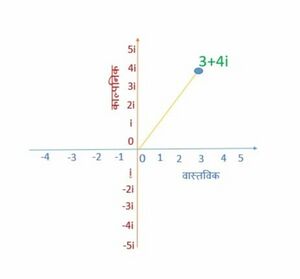
फिर हम एक सम्मिश्र संख्या को आलेखित कर सकते हैं जैसे <math>3+4i</math> : | फिर हम एक सम्मिश्र संख्या को आलेखित कर सकते हैं जैसे <math>3+4i</math> : | ||
Revision as of 12:10, 29 October 2024
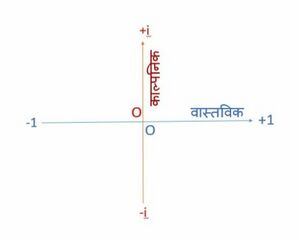
गणित में, सम्मिश्र तल एक ऐसा तल है जो सम्मिश्र संख्याओं से निर्मित होता है। इसमें कार्टेशियन निर्देशांक प्रणाली होती है, जिसमें क्षैतिज -अक्ष को वास्तविक अक्ष कहा जाता है और यह वास्तविक संख्याओं को दर्शाता है, जबकि ऊर्ध्वाधर -अक्ष को काल्पनिक अक्ष कहा जाता है और यह काल्पनिक संख्याओं का प्रतिनिधित्व करता है। सम्मिश्र तल के माध्यम से सम्मिश्र संख्याओं की ज्यामितीय व्याख्या संभव होती है।
इसके अतिरिक्त सम्मिश्र संख्याएँ सदिश की तरह जोड़ती हैं। दो सम्मिश्र संख्याओं का गुणन ध्रुवीय निर्देशांक में सरलता से व्यक्त किया जा सकता है: गुणनफल का परिमाण (या मापांक) दोनों संख्याओं के परिमाणों का गुणनफल होता है, और गुणनफल का कोण (या तर्क) दोनों संख्याओं के कोणों का योग होता है। विशेष रूप से, मापांक 1 वाली किसी सम्मिश्र संख्या से गुणा करने पर यह एक घूर्णन की तरह कार्य करती है।
सम्मिश्र समतल को कभी-कभी आर्गैंड समतल या गॉस समतल कहा जाता है।
सम्मिश्र संख्या एक वास्तविक संख्या और एक काल्पनिक संख्या का संयोजन है:
वास्तविक संख्या वह संख्या है जिसका प्रयोग हम प्रतिदिन करते हैं।
उदाहरण : , , ,
जब हम एक वास्तविक संख्या का वर्ग करते हैं तो हमें सकारात्मक (या शून्य) परिणाम मिलता है:
प्राप्त करने के लिए हम क्या वर्ग कर सकते हैं?
का वर्ग करना काम नहीं करता क्योंकि ऋणात्मक को गुणा करने पर धनात्मक प्राप्त होता है: , और कोई अन्य वास्तविक संख्या भी काम नहीं करती।
तो ऐसा लगता है कि गणित अधूरा है, लेकिन हम इस कमी को इस कल्पना से पूरा कर सकते हैं कि एक संख्या है, जिसे स्वयं से गुणा करने पर -1 प्राप्त होता है
(इसे काल्पनिक के लिए कहें):
एक काल्पनिक संख्या, जब वर्ग की जाती है तो नकारात्मक परिणाम देती है
उदाहरण :
और साथ में:
एक सम्मिश्र संख्या एक वास्तविक संख्या और एक काल्पनिक संख्या का संयोजन है
उदाहरण :
समतल पर सम्मिश्र संख्या रखना
आप संख्या रेखा से परिचित होंगे:
लेकिन हम जैसी सम्मिश्र संख्या कहाँ रखेंगे?
आइए वास्तविक संख्या रेखा को हमेशा की तरह बाएँ-दाएँ घुमाएँ और काल्पनिक संख्या रेखा को ऊपर-नीचे करें:
फिर हम एक सम्मिश्र संख्या को आलेखित कर सकते हैं जैसे :
• इकाइयाँ (वास्तविक अक्ष) के साथ,
और इकाइयाँ ऊपर (काल्पनिक अक्ष)।
और यहाँ है:
• इकाइयाँ (वास्तविक अक्ष) के साथ,
और इकाइयाँ नीचे (काल्पनिक अक्ष)।