मध्य-बिंदु प्रमेय: Difference between revisions
(added content) |
|||
| Line 17: | Line 17: | ||
== मध्यबिंदु प्रमेय का व्युत्क्रम == | == मध्यबिंदु प्रमेय का व्युत्क्रम == | ||
'''कथन:''' The converse of midpoint theorem states that "the line drawn through the midpoint of one side of a triangle that is parallel to another side will bisect the third side". We prove the converse of mid point theorem by contradiction. | |||
''' | |||
=== | === मध्य बिंदु प्रमेय का प्रमाण व्युत्क्रम === | ||
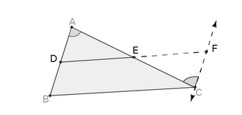
Consider a triangle <math>ABC</math>, and let <math>D</math> be the midpoint of <math>AB</math>. A line through <math>D</math> parallel to <math>BC</math> meets <math>BC</math> at <math>E</math>, as shown in the Fig. 2 below:. | Consider a triangle <math>ABC</math>, and let <math>D</math> be the midpoint of <math>AB</math>. A line through <math>D</math> parallel to <math>BC</math> meets <math>BC</math> at <math>E</math>, as shown in the Fig. 2 below:. | ||
[[File:Midpoint theorem - converse.jpg|alt=Fig. 2|thumb|Fig. 2|none]] | [[File:Midpoint theorem - converse.jpg|alt=Fig. 2|thumb|Fig. 2|none]] | ||
''' | '''दिया गया है:''' <math>\triangle ABC</math> में, <math>D</math>, <math>AB</math> का मध्यबिंदु है और <math>DE \parallel BC</math>। | ||
''' | '''सिद्ध करना:''' <math>E</math>, <math>AC</math> का मध्यबिंदु है (अर्थात,<math>AE=CE</math>) | ||
''' | '''संरचना :''' <math>C</math> से होकर <math>AB</math> के समांतर एक रेखा खींचें जो विस्तारित <math>DE</math> से <math>F</math> पर मिलती है | ||
{| class="wikitable" | {| class="wikitable" | ||
! colspan="2" | | ! colspan="2" |मध्यबिंदु प्रमेय के व्युत्क्रम का प्रमाण | ||
|- | |- | ||
|1. <math>BCFD</math> | |1. <math>BCFD</math> एक समांतर चतुर्भुज है | ||
|<math>DE \parallel BC</math> ( | |<math>DE \parallel BC</math> (दिया गया है) और <math>BD \parallel CF</math> (संरचना द्वारा) | ||
|- | |- | ||
|2. <math>BD =CF</math> | |2. <math>BD =CF</math> | ||
| | |समांतर चतुर्भुज की सम्मुख भुजाएँ बराबर होती हैं | ||
|- | |- | ||
|3.<math>AD=BD</math> | |3.<math>AD=BD</math> | ||
|D | |D, AB का मध्यबिंदु है (दिया गया है) | ||
|- | |- | ||
|4. <math>AD=CF</math> | |4. <math>AD=CF</math> | ||
| | |2 और 3 से | ||
|- | |- | ||
| | |तुलना करें <math>\triangle AED</math> के साथ <math>\triangle CEF</math>: | ||
| | | | ||
|- | |- | ||
|5. <math>\angle DAE=\angle ECF</math> | |5. <math>\angle DAE=\angle ECF</math> | ||
| | |वैकल्पिक कोण | ||
|- | |- | ||
|6. <math>\angle DEA=\angle FEC</math> | |6. <math>\angle DEA=\angle FEC</math> | ||
| | |शीर्षाभिमुख कोण | ||
|- | |- | ||
|7.<math>\triangle AED \cong \triangle CEF</math> | |7.<math>\triangle AED \cong \triangle CEF</math> | ||
| | |AAS मानदंड के अनुसार (4, 5, और 6 का उपयोग करके) | ||
|- | |- | ||
|8. <math>AE=CE</math> | |8. <math>AE=CE</math> | ||
| | |CPCTC द्वारा | ||
|} | |} | ||
इससे व्युत्क्रम मध्यबिंदु प्रमेय का प्रमाण पूरा हो जाता है। | |||
[[Category:चतुर्भुज]][[Category:कक्षा-9]][[Category:गणित]] | [[Category:चतुर्भुज]][[Category:कक्षा-9]][[Category:गणित]] | ||
Revision as of 14:22, 1 November 2024
ज्यामिति के क्षेत्र में त्रिभुजों के गुणों से संबंधित महत्वपूर्ण प्रमेयों में से एक को मध्य-बिंदु प्रमेय कहा जाता है।
मध्य-बिंदु प्रमेय के सिद्धांत का उपयोग निर्देशांक ज्यामिति में किया जाता है, जिसमें कहा गया है कि रेखाखंड का मध्यबिंदु अंत बिंदुओं का औसत होता है। इस प्रमेय का उपयोग करके समीकरण को हल करने के लिए 'x' और 'y' निर्देशांक ज्ञात होना चाहिए। मध्य-बिंदु प्रमेय कलन और बीजगणित के क्षेत्र में भी उपयोगी है।
मध्य-बिंदु प्रमेय कथन
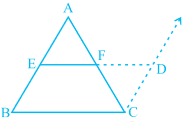
मध्यबिंदु प्रमेय कहता है कि "किसी त्रिभुज में उसकी किन्हीं दो भुजाओं के मध्यबिंदु को मिलाने वाला रेखाखंड उसकी तीसरी भुजा के समांतर कहलाता है और तीसरी भुजा की लंबाई का आधा भी होता है।"
चित्र-1 में दर्शाए गए त्रिभुज में और त्रिभुज की दो भुजाओं के मध्यबिंदु हैं
, and
इसके साथ, हम निम्नलिखित प्रमेयों पर पहुँचते हैं
प्रमेय 1: त्रिभुज की दो भुजाओं के मध्य-बिंदुओं को मिलाने वाला रेखाखंड तीसरी भुजा के समांतर होता है।
प्रमेय 2: त्रिभुज की एक भुजा के मध्य-बिंदु से होकर दूसरी भुजा के समांतर खींची गई रेखा तीसरी भुजा को समद्विभाजित करती है।
मध्यबिंदु प्रमेय का व्युत्क्रम
कथन: The converse of midpoint theorem states that "the line drawn through the midpoint of one side of a triangle that is parallel to another side will bisect the third side". We prove the converse of mid point theorem by contradiction.
मध्य बिंदु प्रमेय का प्रमाण व्युत्क्रम
Consider a triangle , and let be the midpoint of . A line through parallel to meets at , as shown in the Fig. 2 below:.
दिया गया है: में, , का मध्यबिंदु है और ।
सिद्ध करना: , का मध्यबिंदु है (अर्थात,)
संरचना : से होकर के समांतर एक रेखा खींचें जो विस्तारित से पर मिलती है
| मध्यबिंदु प्रमेय के व्युत्क्रम का प्रमाण | |
|---|---|
| 1. एक समांतर चतुर्भुज है | (दिया गया है) और (संरचना द्वारा) |
| 2. | समांतर चतुर्भुज की सम्मुख भुजाएँ बराबर होती हैं |
| 3. | D, AB का मध्यबिंदु है (दिया गया है) |
| 4. | 2 और 3 से |
| तुलना करें के साथ : | |
| 5. | वैकल्पिक कोण |
| 6. | शीर्षाभिमुख कोण |
| 7. | AAS मानदंड के अनुसार (4, 5, और 6 का उपयोग करके) |
| 8. | CPCTC द्वारा |
इससे व्युत्क्रम मध्यबिंदु प्रमेय का प्रमाण पूरा हो जाता है।