मध्य-बिंदु प्रमेय: Difference between revisions
m (added content) |
|||
| (3 intermediate revisions by the same user not shown) | |||
| Line 17: | Line 17: | ||
== मध्यबिंदु प्रमेय का व्युत्क्रम == | == मध्यबिंदु प्रमेय का व्युत्क्रम == | ||
'''कथन:''' मध्यबिंदु प्रमेय के व्युत्क्रम में कहा गया है कि "किसी त्रिभुज की एक भुजा के मध्यबिंदु से होकर दूसरी भुजा के समानांतर खींची गई रेखा तीसरी भुजा को समद्विभाजित करेगी"। हम मध्यबिंदु प्रमेय के व्युत्क्रम को विरोधाभास द्वारा सिद्ध करते हैं। | |||
''' | |||
=== | === मध्य बिंदु प्रमेय का प्रमाण व्युत्क्रम === | ||
एक त्रिभुज <math>ABC</math> पर विचार करें, और <math>D</math> को <math>AB</math> का मध्यबिंदु मान लें। <math>D</math> से होकर <math>BC</math> के समांतर एक रेखा <math>BC</math> को <math>E</math> पर मिलती है, जैसा कि नीचे चित्र 2 में दिखाया गया है:। | |||
Fig. 2 below:. | |||
[[File:Midpoint theorem - converse.jpg|alt=Fig. 2|thumb|चित्र. 2|none]] | |||
''' | '''दिया गया है:''' <math>\triangle ABC</math> में, <math>D</math>, <math>AB</math> का मध्यबिंदु है और <math>DE \parallel BC</math>। | ||
''' | '''सिद्ध करना:''' <math>E</math>, <math>AC</math> का मध्यबिंदु है (अर्थात,<math>AE=CE</math>) | ||
'''संरचना :''' <math>C</math> से होकर <math>AB</math> के समांतर एक रेखा खींचें जो विस्तारित <math>DE</math> से <math>F</math> पर मिलती है | |||
{| class="wikitable" | {| class="wikitable" | ||
! colspan="2" | | ! colspan="2" |मध्यबिंदु प्रमेय के व्युत्क्रम का प्रमाण | ||
|- | |- | ||
|1. <math>BCFD</math> | |1. <math>BCFD</math> एक समांतर चतुर्भुज है | ||
|<math>DE \parallel BC</math> ( | |<math>DE \parallel BC</math> (दिया गया है) और <math>BD \parallel CF</math> (संरचना द्वारा) | ||
|- | |- | ||
|2. <math>BD =CF</math> | |2. <math>BD =CF</math> | ||
| | |समांतर चतुर्भुज की सम्मुख भुजाएँ बराबर होती हैं | ||
|- | |- | ||
|3.<math>AD=BD</math> | |3.<math>AD=BD</math> | ||
|D | |D, AB का मध्यबिंदु है (दिया गया है) | ||
|- | |- | ||
|4. <math>AD=CF</math> | |4. <math>AD=CF</math> | ||
| | |2 और 3 से | ||
|- | |- | ||
| | |तुलना करें <math>\triangle AED</math> के साथ <math>\triangle CEF</math>: | ||
| | | | ||
|- | |- | ||
|5. <math>\angle DAE=\angle ECF</math> | |5. <math>\angle DAE=\angle ECF</math> | ||
| | |वैकल्पिक कोण | ||
|- | |- | ||
|6. <math>\angle DEA=\angle FEC</math> | |6. <math>\angle DEA=\angle FEC</math> | ||
| | |शीर्षाभिमुख कोण | ||
|- | |- | ||
|7.<math>\triangle AED \cong \triangle CEF</math> | |7.<math>\triangle AED \cong \triangle CEF</math> | ||
| | |AAS मानदंड के अनुसार (4, 5, और 6 का उपयोग करके) | ||
|- | |- | ||
|8. <math>AE=CE</math> | |8. <math>AE=CE</math> | ||
| | |CPCTC द्वारा | ||
|} | |} | ||
इससे व्युत्क्रम मध्यबिंदु प्रमेय का प्रमाण पूरा हो जाता है। | |||
== मध्यबिंदु प्रमेय का आवेदन == | |||
मध्यबिंदु प्रमेय का एक दिलचस्प परिणाम यह है कि यदि हम किसी भी त्रिभुज के तीन पक्षों के मध्य बिंदुओं में उपस्थित होते हैं, तो हमें चार (छोटे) बधाई वाले त्रिकोण मिलेंगे, जैसा कि नीचे चित्र 3 में दिखाया गया है: | |||
[[File:Application of Midpoint Theorem.jpg|alt=Fig. 3|thumb|चित्र. 3|none]] | |||
हमारे पास है: <math>\triangle ADE \cong \triangle FED\cong \triangle BDF\cong \triangle EFC</math> | |||
'''प्रमाण:''' चतुर्भुज <math>DEFB</math> पर विचार करें। मध्यबिंदु प्रमेय द्वारा, हमारे पास है: | |||
* <math>DE=\frac{1}{2}BC=BF</math> | |||
* <math>DE \parallel BF</math> | |||
इस प्रकार, <math>DEFB</math> एक समानांतर चतुर्भुज है, जिसका अर्थ है कि <math> \triangle FED\cong \triangle BDF</math>। इसी तरह, हम दिखा सकते हैं कि <math>AEFD</math> और | |||
<math>DECF</math> समांतर चतुर्भुज हैं, और इसलिए सभी चार त्रिभुज सर्वांगसम एक दूसरे के अनुरूप हैं। | |||
[[Category:चतुर्भुज]][[Category:कक्षा-9]][[Category:गणित]] | [[Category:चतुर्भुज]][[Category:कक्षा-9]][[Category:गणित]] | ||
Latest revision as of 07:33, 2 November 2024
ज्यामिति के क्षेत्र में त्रिभुजों के गुणों से संबंधित महत्वपूर्ण प्रमेयों में से एक को मध्य-बिंदु प्रमेय कहा जाता है।
मध्य-बिंदु प्रमेय के सिद्धांत का उपयोग निर्देशांक ज्यामिति में किया जाता है, जिसमें कहा गया है कि रेखाखंड का मध्यबिंदु अंत बिंदुओं का औसत होता है। इस प्रमेय का उपयोग करके समीकरण को हल करने के लिए 'x' और 'y' निर्देशांक ज्ञात होना चाहिए। मध्य-बिंदु प्रमेय कलन और बीजगणित के क्षेत्र में भी उपयोगी है।
मध्य-बिंदु प्रमेय कथन
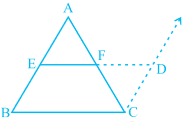
मध्यबिंदु प्रमेय कहता है कि "किसी त्रिभुज में उसकी किन्हीं दो भुजाओं के मध्यबिंदु को मिलाने वाला रेखाखंड उसकी तीसरी भुजा के समांतर कहलाता है और तीसरी भुजा की लंबाई का आधा भी होता है।"
चित्र-1 में दर्शाए गए त्रिभुज में और त्रिभुज की दो भुजाओं के मध्यबिंदु हैं
, and
इसके साथ, हम निम्नलिखित प्रमेयों पर पहुँचते हैं
प्रमेय 1: त्रिभुज की दो भुजाओं के मध्य-बिंदुओं को मिलाने वाला रेखाखंड तीसरी भुजा के समांतर होता है।
प्रमेय 2: त्रिभुज की एक भुजा के मध्य-बिंदु से होकर दूसरी भुजा के समांतर खींची गई रेखा तीसरी भुजा को समद्विभाजित करती है।
मध्यबिंदु प्रमेय का व्युत्क्रम
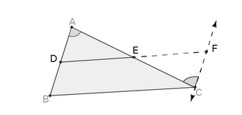
कथन: मध्यबिंदु प्रमेय के व्युत्क्रम में कहा गया है कि "किसी त्रिभुज की एक भुजा के मध्यबिंदु से होकर दूसरी भुजा के समानांतर खींची गई रेखा तीसरी भुजा को समद्विभाजित करेगी"। हम मध्यबिंदु प्रमेय के व्युत्क्रम को विरोधाभास द्वारा सिद्ध करते हैं।
मध्य बिंदु प्रमेय का प्रमाण व्युत्क्रम
एक त्रिभुज पर विचार करें, और को का मध्यबिंदु मान लें। से होकर के समांतर एक रेखा को पर मिलती है, जैसा कि नीचे चित्र 2 में दिखाया गया है:।
Fig. 2 below:.
दिया गया है: में, , का मध्यबिंदु है और ।
सिद्ध करना: , का मध्यबिंदु है (अर्थात,)
संरचना : से होकर के समांतर एक रेखा खींचें जो विस्तारित से पर मिलती है
| मध्यबिंदु प्रमेय के व्युत्क्रम का प्रमाण | |
|---|---|
| 1. एक समांतर चतुर्भुज है | (दिया गया है) और (संरचना द्वारा) |
| 2. | समांतर चतुर्भुज की सम्मुख भुजाएँ बराबर होती हैं |
| 3. | D, AB का मध्यबिंदु है (दिया गया है) |
| 4. | 2 और 3 से |
| तुलना करें के साथ : | |
| 5. | वैकल्पिक कोण |
| 6. | शीर्षाभिमुख कोण |
| 7. | AAS मानदंड के अनुसार (4, 5, और 6 का उपयोग करके) |
| 8. | CPCTC द्वारा |
इससे व्युत्क्रम मध्यबिंदु प्रमेय का प्रमाण पूरा हो जाता है।
मध्यबिंदु प्रमेय का आवेदन
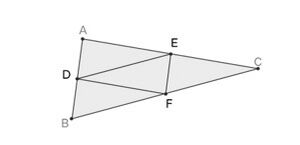
मध्यबिंदु प्रमेय का एक दिलचस्प परिणाम यह है कि यदि हम किसी भी त्रिभुज के तीन पक्षों के मध्य बिंदुओं में उपस्थित होते हैं, तो हमें चार (छोटे) बधाई वाले त्रिकोण मिलेंगे, जैसा कि नीचे चित्र 3 में दिखाया गया है:
हमारे पास है:
प्रमाण: चतुर्भुज पर विचार करें। मध्यबिंदु प्रमेय द्वारा, हमारे पास है:
इस प्रकार, एक समानांतर चतुर्भुज है, जिसका अर्थ है कि । इसी तरह, हम दिखा सकते हैं कि और
समांतर चतुर्भुज हैं, और इसलिए सभी चार त्रिभुज सर्वांगसम एक दूसरे के अनुरूप हैं।