|
|
| Line 28: |
Line 28: |
| यदि कोण समान रहता है तो किसी कोण के त्रिकोणमितीय अनुपातों का मान त्रिभुज की भुजाओं की लंबाई के साथ भिन्न नहीं होता है। | | यदि कोण समान रहता है तो किसी कोण के त्रिकोणमितीय अनुपातों का मान त्रिभुज की भुजाओं की लंबाई के साथ भिन्न नहीं होता है। |
| == त्रिकोणमितीय अनुपात सारणी == | | == त्रिकोणमितीय अनुपात सारणी == |
| In the trigonometric ratios table, we use the values of trigonometric ratios for standard angles <math>0^\circ ,30^\circ,45^\circ,60^\circ ,90^\circ</math>. It is easy to predict the values of the table and to use the table as a reference to calculate values of trigonometric ratios for various other angles, using the trigonometric ratio formulas for existing patterns within trigonometric ratios and even between angles. Now, we will summarize the value of trigonometric ratios for specific angles in the table below:
| | त्रिकोणमितीय अनुपात सारणी में, हम मानक कोणों <math>0^\circ ,30^\circ,45^\circ,60^\circ ,90^\circ</math> के लिए त्रिकोणमितीय अनुपातों के मानों का उपयोग करते हैं। सारणी के मानों की भविष्यवाणी करना और त्रिकोणमितीय अनुपातों के भीतर और यहां तक कि कोणों के बीच विद्यमान प्रतिरूप(पैटर्न) के लिए त्रिकोणमितीय अनुपात सूत्रों का उपयोग करके विभिन्न अन्य कोणों के लिए त्रिकोणमितीय अनुपातों के मानों की गणना करने के लिए संदर्भ के रूप में सारणी का उपयोग करना आसान है। अब, हम नीचे दी गई सारणी में विशिष्ट कोणों के लिए त्रिकोणमितीय अनुपातों के मान को संक्षेप में प्रस्तुत करेंगे: |
| {| class="wikitable" | | {| class="wikitable" |
| |+ | | |+ |
| Line 66: |
Line 66: |
| |<math>1</math> | | |<math>1</math> |
| |<math>\sqrt3</math> | | |<math>\sqrt3</math> |
| |Not defined | | |परिभाषित नहीं |
| |<math>0</math> | | |<math>0</math> |
| |Not defined | | |परिभाषित नहीं |
| |<math>0</math> | | |<math>0</math> |
| |- | | |- |
| |<math>cosec \ \theta</math> | | |<math>cosec \ \theta</math> |
| |Not defined | | |परिभाषित नहीं |
| |<math>2</math> | | |<math>2</math> |
| |<math>\sqrt2</math> | | |<math>\sqrt2</math> |
| |<math>\frac{2}{\sqrt3}</math> | | |<math>\frac{2}{\sqrt3}</math> |
| |<math>1</math> | | |<math>1</math> |
| |Not defined | | |परिभाषित नहीं |
| | -<math>1</math> | | | -<math>1</math> |
| |Not defined | | |परिभाषित नहीं |
| |- | | |- |
| |<math>sec \ \theta</math> | | |<math>sec \ \theta</math> |
| Line 86: |
Line 86: |
| |<math>\sqrt2</math> | | |<math>\sqrt2</math> |
| |<math>2</math> | | |<math>2</math> |
| |Not defined | | |परिभाषित नहीं |
| | -<math>1</math> | | | -<math>1</math> |
| |Not defined | | |परिभाषित नहीं |
| |<math>1</math> | | |<math>1</math> |
| |- | | |- |
| |<math>cot \ \theta</math> | | |<math>cot \ \theta</math> |
| |Not defined | | |परिभाषित नहीं |
| |<math>\sqrt3</math> | | |<math>\sqrt3</math> |
| |<math>1</math> | | |<math>1</math> |
| |<math>\frac{1}{\sqrt3}</math> | | |<math>\frac{1}{\sqrt3}</math> |
| |<math>0</math> | | |<math>0</math> |
| |Not defined | | |परिभाषित नहीं |
| |<math>0</math> | | |<math>0</math> |
| |Not defined | | |परिभाषित नहीं |
| |} | | |} |
|
| |
|
Revision as of 08:36, 4 November 2024
परिचय
किसी समकोण त्रिभुज में किन्हीं दो भुजाओं के अनुपात को त्रिकोणमितीय अनुपात या त्रिकोणमितीय अनुपात कहते हैं। समकोण त्रिभुज में न्यून कोण का त्रिकोणमितीय अनुपात उसकी भुजाओं के कोण और लंबाई के बीच संबंध को व्यक्त करता है।
परिभाषा
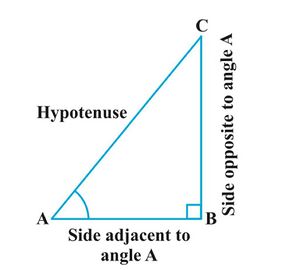
चित्र 1 में दिखाए गए समकोण त्रिभुज  पर विचार करें। यहाँ कोण
पर विचार करें। यहाँ कोण  (कोण
(कोण  ) एक न्यूनकोण है। भुजा
) एक न्यूनकोण है। भुजा  कोण
कोण  के सम्मुख है। इसलिए
के सम्मुख है। इसलिए  कोण
कोण  के विपरीत भुजा है।
के विपरीत भुजा है।  समकोण त्रिभुज
समकोण त्रिभुज  का कर्ण है और भुजा
का कर्ण है और भुजा  कोण
कोण  का भाग है। इसलिए
का भाग है। इसलिए  कोण
कोण  से सटी हुई भुजा है।
से सटी हुई भुजा है।
समकोण त्रिभुज  में कोण
में कोण  के त्रिकोणमितीय अनुपात निम्नानुसार परिभाषित किए गए हैं।
के त्रिकोणमितीय अनुपात निम्नानुसार परिभाषित किए गए हैं।








ध्यान दें: यहां प्रतीक साइन A का उपयोग ''कोण A की साइन'' के संक्षिप्त रूप के रूप में किया गया है। साइन A, ''साइन'' और "A" का गुणनफल नहीं है। ''साइन'' को A से अलग किया गया है। अन्य त्रिकोणमितीय अनुपात के लिए भी इसी तरह की व्याख्याएं की जाती हैं।
यदि कोण समान रहता है तो किसी कोण के त्रिकोणमितीय अनुपातों का मान त्रिभुज की भुजाओं की लंबाई के साथ भिन्न नहीं होता है।
त्रिकोणमितीय अनुपात सारणी
त्रिकोणमितीय अनुपात सारणी में, हम मानक कोणों  के लिए त्रिकोणमितीय अनुपातों के मानों का उपयोग करते हैं। सारणी के मानों की भविष्यवाणी करना और त्रिकोणमितीय अनुपातों के भीतर और यहां तक कि कोणों के बीच विद्यमान प्रतिरूप(पैटर्न) के लिए त्रिकोणमितीय अनुपात सूत्रों का उपयोग करके विभिन्न अन्य कोणों के लिए त्रिकोणमितीय अनुपातों के मानों की गणना करने के लिए संदर्भ के रूप में सारणी का उपयोग करना आसान है। अब, हम नीचे दी गई सारणी में विशिष्ट कोणों के लिए त्रिकोणमितीय अनुपातों के मान को संक्षेप में प्रस्तुत करेंगे:
के लिए त्रिकोणमितीय अनुपातों के मानों का उपयोग करते हैं। सारणी के मानों की भविष्यवाणी करना और त्रिकोणमितीय अनुपातों के भीतर और यहां तक कि कोणों के बीच विद्यमान प्रतिरूप(पैटर्न) के लिए त्रिकोणमितीय अनुपात सूत्रों का उपयोग करके विभिन्न अन्य कोणों के लिए त्रिकोणमितीय अनुपातों के मानों की गणना करने के लिए संदर्भ के रूप में सारणी का उपयोग करना आसान है। अब, हम नीचे दी गई सारणी में विशिष्ट कोणों के लिए त्रिकोणमितीय अनुपातों के मान को संक्षेप में प्रस्तुत करेंगे:

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
-
|

|

|

|

|

|

|

|
-
|

|

|

|

|

|

|

|
परिभाषित नहीं
|

|
परिभाषित नहीं
|

|

|
परिभाषित नहीं
|

|

|

|

|
परिभाषित नहीं
|
-
|
परिभाषित नहीं
|

|

|

|

|

|
परिभाषित नहीं
|
-
|
परिभाषित नहीं
|

|

|
परिभाषित नहीं
|

|

|

|

|
परिभाषित नहीं
|

|
परिभाषित नहीं
|
पूरक कोणों की त्रिकोणमितीय अनुपात सर्वसमिकाएं
पूरक कोण दो कोणों का एक युग्म है, जिसका योग  के समान ोता है। कोण
के समान ोता है। कोण  का पूरक (
का पूरक ( है। पूरक कोणों के त्रिकोणमितीय अनुपात हैं:
है। पूरक कोणों के त्रिकोणमितीय अनुपात हैं:





 ।
।