कुछ फलन और उनके आलेख: Difference between revisions

Revision as of 21:47, 7 November 2024

फलन और कुछ आलेख

चित्र-1 f(x)=x

(i) तत्समक फलन: मान लीजिए $R$ वास्तविक संख्याओं का समुच्चय है। $y=f(x)$ , प्रत्येक $x\in R$ द्वारा परिभाषित वास्तविक मान फलन $f:R\rightarrow R$ है। इस प्रकार के फलन को तत्समक फलन कहते हैं। यहाँ पर $f$ के प्रांत तथा परिसर $R$ हैं। इसका आलेख एक सरल रेखा होता है(चित्र-1)। यह रेखा मूल बिंदु से हो कर जाती है।

चित्र-2 f(x)=3

(ii) अचर फलन: $y=f(x)=c$ जहाँ $c$ एक अचर है और प्रत्येक $x\in R$ द्वारा परिभाषित एक वास्तविक मान फलन $f:R\rightarrow R$ है। यहाँ पर $f$ का प्रांत $R$ है और उसका परिसर $\{c\}$ है। $f$ का आलेख $x$ - अक्ष के समांतर एक रेखा है, उदाहरण के लिए यदि $f(x)=3$ प्रत्येक $x\in R$ है, तो इसका आलेख (चित्र- 2) में दर्शाई रेखा है।

(iii) बहुपद फलन या बहुपदीय फलन: फलन $f:R\rightarrow R$ , एक बहुपदीय फलन कहलाता है, यदि $R$ के प्रत्येक $x$ के लिए, $y=f(x)=a_{0}+a_{1}x+a_{2}x^{2}+....+a_{n}x^{n}$ , जहाँ ” $n$ " एक ऋणेतर पूर्णांक है तथा $a_{0},a_{1},a_{2},.....a_{n}\in R$ ।

$f(x)=x^{3}-x^{2}+2$ , और $g(x)=x^{4}+{\sqrt {2}}x$ , द्वारा परिभाषित फलन एक बहुपदीय फलन है जब कि $h(x)=x^{\frac {2}{3}}+2x$ द्वारा परिभाषित फलन $h$ , बहुपदीय फलन नहीं है।

(iv) परिमेय फलन: ${\frac {f(x)}{g(x)}}$ के प्रकार के फलन जहाँ $f(x)$ तथा $g(x)$

एक प्रांत में, $x$ के परिभाषित बहुपदीय फलन हैं, जिसमें $g(x)\neq 0$ परिमेय फलन कहलाते हैं।

उदाहरण एक वास्तविक मान फलन $f:R-\{0\}\rightarrow R$ की परिभाषा $f(x)={\frac {1}{x}}$ , $x\in R-\{0\}$ द्वारा कीजिए। इस परिभाषा का प्रयोग करके निम्नलिखित तालिका को पूर्ण करेंगे। इस फलन का प्रांत तथा परिसर क्या हैं,इसका भी ज्ञात करेंगे।

चित्र-3 f(x)=1/x

हल पूर्ण की गई तालिका इस प्रकार है:


$x$	$-2$	$-1.5$	$-1$	$-0.5$	$0.25$	$0.5$	$1$	$1.5$	$2$
$y={\frac {1}{x}}$	$-0.5$	$-0.67$	$-1$	$-2$	$4$	$2$	$1$	$0.67$	$0.5$

इसका प्रांत, शून्य के अतिरिक्त समस्त वास्तविक संख्याएँ हैं तथा इसका परिसर भी शून्य के अतिरिक्त समस्त वास्तविक संख्याएँ हैं। $f$ का आलेख चित्र-3 में प्रदर्शित है।

(v) मापांक फलन (Modulus functions) f (x) = bxl प्रत्येक X ER द्वारा परिभाषित फलन fRR, मापांक फलन कहलाता है। x के प्रत्येक ऋणेत्तर मान के लिए f(x), x के बराबर होता है। परंतु x के ऋण मानों के लिए, f(x) का मान x के मान के ऋण के बराबर होता है,

[xx 20 f(x)=- -x, x < 0

अर्थात्

मापांक फलन का आलेख आकृति 2.13 में दिया है । मापांक फलन को निरपेक्ष मान फलन भी कहते हैं।

(vi)

चिह्न फलन (Signum functions) प्रत्येक xER, के लिए

1, यदि x > 0

f (x) = 0, यदि x = 0

- 1, यदि x<0

द्वारा परिभाषित फलन f: RR चिह्न फलन कहलाता है। चिह्न फलन का प्रांत R है। परिसर समुच्चय (-1, 0, 1] है। आकृति 2.14 में चिह्न फलन का आलेख दर्शाया गया है। (vii) महत्तम पूर्णांक फलन (Greatest integer functions) f(x) = [x], xER द्वारा परिभाषित फलन

x'←

J=-1←

f(x) = | यदि x

x

आकृ

f R→ R, x से कम या x के बराबर महत्तम पूर्णांक का मान ग्रहण (धारण) करता है ऐसा फलन महत्तम पूर्णांक फलन कहलाता है।

[x], की परिभाषा से हम देख सकते हैं कि

[x] = 1 यदि - 1 [x] =

0 यदि 05 x<1

[x] =

1 यदि 1 ≤ x<2

[x] =

2 यदि 2≤ x < 3 इत्यदि

इस फलन का आलेख आकृति 2.15 में दर्शाया गया है।

@@ Line 2: / Line 2: @@
 [[Category:गणित]]
 [[Category:कक्षा-11]]
+== फलन और कुछ आलेख ==
+[[File:चित्र-1 f(x)=x.jpg|thumb|चित्र-1 f(x)=x]]
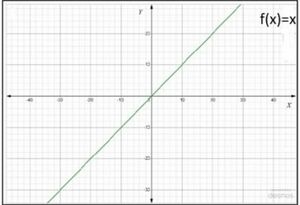
+(i) '''तत्समक फलन:'''  मान लीजिए <math>R</math> वास्तविक संख्याओं का समुच्चय है। <math>y=f(x)</math>, प्रत्येक <math>x\in R</math> द्वारा परिभाषित वास्तविक मान फलन <math>f:R\rightarrow R</math>  है। इस प्रकार के फलन को तत्समक फलन कहते हैं। यहाँ पर <math>f</math> के प्रांत तथा परिसर <math>R</math> हैं। इसका आलेख एक सरल रेखा होता है(चित्र-1)। यह रेखा मूल बिंदु से हो कर जाती है।
+[[File:फलन f(x)=3.jpg|thumb|चित्र-2 f(x)=3]]
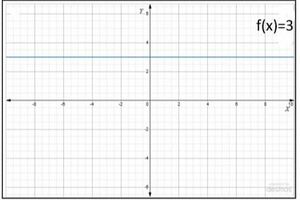
+(ii) '''अचर फलन:''' <math>y=f(x)=c</math>  जहाँ <math>c</math> एक अचर है और प्रत्येक <math>x\in R</math> द्वारा परिभाषित एक वास्तविक मान फलन <math>f:R\rightarrow R</math> है। यहाँ पर <math>f</math> का प्रांत <math>R</math> है और उसका परिसर <math>\{c\}</math> है। <math>f</math> का आलेख <math>x</math>- अक्ष के समांतर एक रेखा है, उदाहरण के लिए यदि <math>f(x)=3</math> प्रत्येक <math>x\in R</math> है, तो इसका आलेख (चित्र- 2) में दर्शाई रेखा है।
+(iii) '''बहुपद फलन या बहुपदीय फलन:'''  फलन <math>f:R\rightarrow R</math>, एक बहुपदीय फलन कहलाता है, यदि <math>R</math> के प्रत्येक <math>x</math> के लिए, <math>y=f(x)=a_0+a_1x+a_2x^2+....+a_nx^n</math>, जहाँ ”<math>n</math>" एक ऋणेतर पूर्णांक है तथा <math>a_0,a_1,a_2,.....a_n\in R</math> ।
+<math>f(x)=x^3-x^2+2  </math>, और <math> g(x)=x^4+\sqrt{2}x</math>, द्वारा परिभाषित फलन एक बहुपदीय फलन है जब कि <math>h(x)=x^\frac{2}{3}+2x</math> द्वारा परिभाषित फलन <math>h</math>, बहुपदीय फलन नहीं है।
+(iv) '''परिमेय फलन:'''  <math>\frac{f(x)}{g(x)}</math> के प्रकार के फलन जहाँ <math>f(x)</math> तथा <math>g(x)</math>
+एक प्रांत में, <math>x</math> के परिभाषित बहुपदीय फलन हैं, जिसमें <math>g(x)\neq 0</math> परिमेय फलन कहलाते हैं।
+'''उदाहरण'''  एक वास्तविक मान फलन <math>f:R-\{0\}\rightarrow R</math> की परिभाषा  <math>f(x)=\frac{1}{x}</math>, <math>x\in R-\{0\}</math> द्वारा कीजिए। इस परिभाषा का प्रयोग करके निम्नलिखित तालिका को पूर्ण करेंगे। इस फलन का प्रांत तथा परिसर क्या हैं,इसका भी ज्ञात करेंगे।
+[[File:F(x)=1byx.jpg|thumb|चित्र-3 f(x)=1/x]]
+'''हल'''  पूर्ण की गई तालिका इस प्रकार है:
+{| class="wikitable"
+|+
+!<math>x</math>
+!<math>-2</math>
+!<math>-1.5</math>
+!<math>-1</math>
+!<math>-0.5</math>
+!<math>0.25</math>
+!<math>0.5</math>
+!<math>1</math>
+!<math>1.5</math>
+!<math>2</math>
+|-
+|<math>y=\frac{1}{x}</math>
+|<math>-0.5</math>
+|<math>-0.67</math>
+|<math>-1</math>
+|<math>-2</math>
+|<math>4</math>
+|<math>2</math>
+|<math>1</math>
+|<math>0.67</math>
+|<math>0.5</math>
+|}
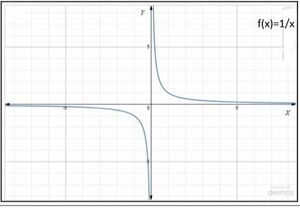
+इसका प्रांत, शून्य के अतिरिक्त समस्त वास्तविक संख्याएँ हैं तथा इसका परिसर भी शून्य के अतिरिक्त समस्त वास्तविक संख्याएँ हैं। <math>f</math> का आलेख चित्र-3 में प्रदर्शित है।
+(v) मापांक फलन (Modulus functions) f (x) = bxl प्रत्येक X ER द्वारा परिभाषित फलन fRR, मापांक फलन कहलाता है। x के प्रत्येक ऋणेत्तर मान के लिए f(x), x के बराबर होता है। परंतु x के ऋण मानों के लिए, f(x) का मान x के मान के ऋण के बराबर होता है,
+[xx 20 f(x)=- -x, x < 0
+अर्थात्
+मापांक फलन का आलेख आकृति 2.13 में दिया है । मापांक फलन को निरपेक्ष मान फलन भी कहते हैं।
+(vi)
+चिह्न फलन (Signum functions) प्रत्येक xER, के लिए
+, यदि x > 0
+f (x) = 0, यदि x = 0
+- 1, यदि x<0
+द्वारा परिभाषित फलन f: RR चिह्न फलन कहलाता है। चिह्न फलन का प्रांत R है। परिसर समुच्चय (-1, 0, 1] है। आकृति 2.14 में चिह्न फलन का आलेख दर्शाया गया है। (vii) महत्तम पूर्णांक फलन (Greatest integer functions) f(x) = [x], xER द्वारा परिभाषित फलन
+x'←
+J=-1←
+f(x) = | यदि x
+x
+आकृ
+f R→ R, x से कम या x के बराबर महत्तम पूर्णांक का मान ग्रहण (धारण) करता है ऐसा फलन महत्तम पूर्णांक फलन कहलाता है।
+[x], की परिभाषा से हम देख सकते हैं कि
+[x] = 1 यदि - 1 [x] =
+यदि 05 x<1
+[x] =
+यदि 1 ≤ x<2
+[x] =
+यदि 2≤ x < 3 इत्यदि
+इस फलन का आलेख आकृति 2.15 में दर्शाया गया है।
+[[Category:संबंध और फलन]][[Category:कक्षा-11]][[Category:गणित]][[Category:गणित]]