डिग्री माप: Difference between revisions
(content modified) |
|||
| (One intermediate revision by the same user not shown) | |||
| Line 56: | Line 56: | ||
आंतरिक रीडिंग और बाहरी रीडिंग एक दूसरे के पूरक हैं। यानी, वे मिलकर <math>180^\circ</math> डिग्री का कोण बनाते हैं। | आंतरिक रीडिंग और बाहरी रीडिंग एक दूसरे के पूरक हैं। यानी, वे मिलकर <math>180^\circ</math> डिग्री का कोण बनाते हैं। | ||
== | == महत्वपूर्ण टिप्पणियाँ == | ||
* डिग्री कोणों को मापने की एक इकाई है। | |||
* हम निम्नलिखित सूत्रों का उपयोग करके डिग्री में कोण को रेडियन में कोण में और इसके विपरीत परिवर्तित कर सकते हैं: | |||
# डिग्री में कोण = रेडियन में कोण <math>\times\frac{180^\circ}{\pi}</math> | |||
# रेडियन में कोण = डिग्री में कोण <math>\times\frac{\pi}{180^\circ} </math> | |||
* एक पूरा घुमाव <math>360</math> डिग्री के समान होता है। | |||
[[Category:त्रिकोणमितीय फलन]] | [[Category:त्रिकोणमितीय फलन]] | ||
[[Category:कक्षा-11]] | [[Category:कक्षा-11]] | ||
[[Category:गणित]] | [[Category:गणित]] | ||
Latest revision as of 22:10, 12 November 2024
ज्यामिति में, रेखाएँ और कोण मूल शब्द हैं जो विषय की नींव स्थापित करते हैं। कोण को दो किरणों द्वारा बनाई गई एक आकृति के रूप में परिभाषित किया जाता है जो एक सामान्य समापन बिंदु पर मिलती हैं। इन्हें एक चांदे(प्रोट्रैक्टर) का उपयोग करके डिग्री में मापा जाता है। सभी ज्यामितीय आकृतियों में रेखाएँ और कोण होते हैं।
परिभाषा
डिग्री एक इकाई है जिसका उपयोग कोण के माप को दर्शाने के लिए किया जाता है। कोणों के मापन की दो सामान्य रूप से इस्तेमाल की जाने वाली इकाइयाँ हैं जो रेडियन और डिग्री हैं। व्यावहारिक ज्यामिति के विषय में, हम प्रायः कोण को डिग्री में मापते हैं। डिग्री को ° (डिग्री प्रतीक) द्वारा दर्शाया जाता है। डिग्री में एक पूर्ण कोण का माप डिग्री (जिसे भी लिखा जाता है) है जो एक पूर्ण घूर्णन का माप है।
डिग्री कोणों को मापने की एक इकाई है। यह इकाई नहीं है क्योंकि कोणों को मापने की इकाई रेडियन है। साधारणतः, ज्यामिति में, हम कोण को डिग्री में मापने के लिए कोणमापक(प्रोट्रैक्टर) का उपयोग करते हैं। कोणमापक का उपयोग प्रायः विध्यालयों में विभिन्न गणितीय समस्याओं को हल करने के लिए कोणों को मापने के लिए किया जाता है।
इस लेख में, हम डिग्री के रूप में जानी जाने वाली कोण की इकाई, उसके प्रतीक और उसकी परिभाषा पर चर्चा करेंगे। अवधारणा को बेहतर ढंग से समझने के लिए हम डिग्री में कोण का माप देते हुए कुछ हल उदाहरण देंगे और देखेंगे कि कोण के माप को दर्शाने के लिए डिग्री के प्रतीक का उपयोग कैसे किया जाता है।
डिग्री माप
यदि प्रारंभिक भुजा से अंतिम भुजा का घुमाव एक पूर्ण परिक्रमण का वाँ भाग हो तो हम कोण का माप एक डिग्री कहते हैं, इसे से लिखते हैं।
एक डिग्री को मिनट में तथा एक मिनट को सेकंड में विभाजित किया जाता है। एक डिग्री का साठवाँ भाग एक मिनट कहलाता है, इसे से लिखते हैं तथा एक मिनट का साठवाँ भाग एक सेकंड कहलाता है, इसे से लिखते हैं। अर्थात्
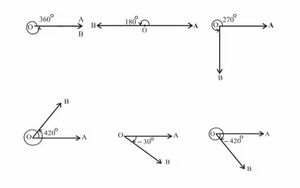
कुछ कोण जिनका माप है उन्हें चित्र में दर्शाया गया है।
डिग्री का प्रतीक
डिग्री के प्रतीक के रूप में हम किसी संख्या के बाद उसके ऊपरी दाएँ कोने में एक छोटा वृत्त () उपयोग करते हैं। डिग्री के प्रतीक का इस्तेमाल कैसे किया जाता है, यह समझने के लिए आइए कुछ उदाहरण देखें:
डिग्री =
डिग्री =
रेडियन = डिग्री =
रेडियन = डिग्री =
डिग्री में कोण
गणित में कोण के माप की इकाई को डिग्री कहा जाता है। कोण की डिग्री को प्रोट्रैक्टर नामक उपकरण का उपयोग करके मापा जाता है। एक पूरा वृत्त पर घूमता है और कोणों को अलग-अलग कोणों पर मापा जा सकता है, जो अलग-अलग डिग्री दिखाते हैं जैसे कि , , , इत्यादि। एक चक्कर को समान भागों में विभाजित किया जाता है, और प्रत्येक भाग को डिग्री कहा जाता है। हम एक डिग्री को वृत्त ° से दर्शाते हैं। उदाहरण के लिए, का मतलब डिग्री है। जिस कोण का माप डिग्री में दिया जाता है उसे डिग्री में कोण कहा जाता है।
हम डिग्री की संख्या के अनुसार कोणों को निम्नानुसार वर्गीकृत कर सकते हैं:
समकोण - समकोण का माप डिग्री () होता है।
अधिक कोण - अधिक कोण का माप से अधिक और से कम होता है
न्यून कोण - अधिक कोण का माप से कम और से अधिक होता है
सीधा कोण - सीधे कोण का माप होता है
प्रतिवर्ती कोण - प्रतिवर्ती कोण का माप से अधिक और से कम होता है।
पूर्ण कोण - सीधे कोण का माप होता है
कोण को डिग्री में मापना
कोण को डिग्री में मापने के लिए सबसे अच्छा उपकरण कोणमापक है। कोणमापक के घुमावदार किनारे को समान भागों में विभाजित किया गया है।
कोणमापक पर संख्याओं के दो समुच्चय होते हैं:
- एक दक्षिणावर्त दिशा में
- दूसरा वामावर्त दिशा में
अगर आप ध्यान से देखें, तो कोणमापक पर बाहरी किनारे पर बाएं से दाएं से तक और अंदर की तरफ से तक डिग्री अंकित होती हैं।
आंतरिक रीडिंग और बाहरी रीडिंग एक दूसरे के पूरक हैं। यानी, वे मिलकर डिग्री का कोण बनाते हैं।
महत्वपूर्ण टिप्पणियाँ
- डिग्री कोणों को मापने की एक इकाई है।
- हम निम्नलिखित सूत्रों का उपयोग करके डिग्री में कोण को रेडियन में कोण में और इसके विपरीत परिवर्तित कर सकते हैं:
- डिग्री में कोण = रेडियन में कोण
- रेडियन में कोण = डिग्री में कोण
- एक पूरा घुमाव डिग्री के समान होता है।