रेडियन माप: Difference between revisions
(added content) |
No edit summary |
||
| (One intermediate revision by the same user not shown) | |||
| Line 2: | Line 2: | ||
[[Category:कक्षा-11]] | [[Category:कक्षा-11]] | ||
[[Category:गणित]] | [[Category:गणित]] | ||
रेडियन एक इकाई है जिसका उपयोग कोणों को मापने के लिए किया जाता है। कोणों को मापने के लिए हमारे पास दो इकाइयाँ हैं: डिग्री और रेडियन। इस चरण तक, आप कोणों के आकार को मापने के लिए डिग्री का उपयोग कर रहे होंगे। हालाँकि, कई कारणों से, उन्नत गणित में कोण माप को प्रायः डिग्री प्रणाली से अलग इकाई प्रणाली का उपयोग करके वर्णित किया जाता है। इस प्रणाली को रेडियन प्रणाली के रूप में जाना जाता है। क्या आप जानते हैं कि 1995 से पहले कोणों को मापने के लिए रेडियन <math>SI</math> पूरक इकाई थी? बाद में इसे व्युत्पन्न इकाई में बदल दिया गया। | रेडियन एक इकाई है जिसका उपयोग [[कोण|कोणों]] को मापने के लिए किया जाता है। कोणों को मापने के लिए हमारे पास दो इकाइयाँ हैं: डिग्री और रेडियन। इस चरण तक, आप कोणों के आकार को मापने के लिए डिग्री का उपयोग कर रहे होंगे। हालाँकि, कई कारणों से, उन्नत गणित में कोण माप को प्रायः डिग्री प्रणाली से अलग इकाई प्रणाली का उपयोग करके वर्णित किया जाता है। इस प्रणाली को रेडियन प्रणाली के रूप में जाना जाता है। क्या आप जानते हैं कि 1995 से पहले कोणों को मापने के लिए रेडियन <math>SI</math> पूरक इकाई थी? बाद में इसे व्युत्पन्न इकाई में बदल दिया गया। | ||
आइए, रेडियन सूत्र, चाप लंबाई सूत्र और कोण को रेडियन से डिग्री और डिग्री से रेडियन में बदलने के तरीके के बारे में विस्तार से जानें। | आइए, रेडियन सूत्र, चाप लंबाई सूत्र और कोण को रेडियन से डिग्री और डिग्री से रेडियन में बदलने के तरीके के बारे में विस्तार से जानें। | ||
== परिचय == | == परिचय == | ||
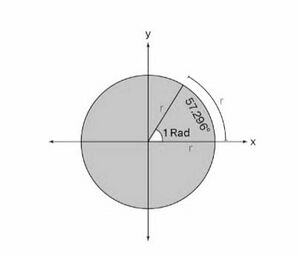
[[File:रेडियन.jpg|thumb|चित्र-1 रेडियन]] | |||
रेडियन एक <math>SI</math> इकाई है जिसका उपयोग कोणों को मापने के लिए किया जाता है और एक रेडियन एक वृत्त के केंद्र पर एक चाप द्वारा बनाया गया कोण होता है जिसकी लंबाई वृत्त की त्रिज्या के समान होती है। एक रेडियन जो नीचे दिखाया गया है, लगभग <math>57.296</math> डिग्री के समान है। जब हम त्रिज्या के संदर्भ में कोण की गणना करना चाहते हैं तो हम डिग्री के स्थान पर रेडियन का उपयोग करते हैं। जैसे '<math>^c</math>' का उपयोग डिग्री को दर्शाने के लिए किया जाता है, वैसे ही रेडियन को दर्शाने के लिए <math>rad</math> या <math>^c</math> का उपयोग किया जाता है। उदाहरण के लिए, 1.5 रेडियन को 1.5 <math>rad</math> या 1.5<math>^c</math> के रूप में लिखा जाता है। | रेडियन एक <math>SI</math> इकाई है जिसका उपयोग कोणों को मापने के लिए किया जाता है और एक रेडियन एक वृत्त के केंद्र पर एक चाप द्वारा बनाया गया कोण होता है जिसकी लंबाई वृत्त की त्रिज्या के समान होती है। एक रेडियन जो नीचे दिखाया गया है, लगभग <math>57.296</math> डिग्री के समान है। जब हम त्रिज्या के संदर्भ में कोण की गणना करना चाहते हैं तो हम डिग्री के स्थान पर रेडियन का उपयोग करते हैं। जैसे '<math>^c</math>' का उपयोग डिग्री को दर्शाने के लिए किया जाता है, वैसे ही रेडियन को दर्शाने के लिए <math>rad</math> या <math>^c</math> का उपयोग किया जाता है। उदाहरण के लिए, 1.5 रेडियन को 1.5 <math>rad</math> या 1.5<math>^c</math> के रूप में लिखा जाता है। | ||
| Line 22: | Line 23: | ||
== रेडियन सूत्र == | == रेडियन सूत्र == | ||
[[File:चाप द्वारा रेडियन में बनाया गया कोण.jpg|thumb|चित्र-2 चाप द्वारा रेडियन में बनाया गया कोण]] | |||
हम पहले ही सीख चुके हैं कि <math>1</math> रेडियन उस वृत्त के चाप द्वारा बनाए गए कोण के बराबर होता है जिसकी लंबाई वृत्त की त्रिज्या के बराबर होती है। इस प्रकार, एक वृत्त के रेडियन में चाप द्वारा बनाया गया कोण '''चाप की लंबाई''' और वृत्त की त्रिज्या के '''अनुपात''' के रूप में परिभाषित किया जाता है। | हम पहले ही सीख चुके हैं कि <math>1</math> रेडियन उस वृत्त के चाप द्वारा बनाए गए कोण के बराबर होता है जिसकी लंबाई वृत्त की त्रिज्या के बराबर होती है। इस प्रकार, एक वृत्त के रेडियन में चाप द्वारा बनाया गया कोण '''चाप की लंबाई''' और वृत्त की त्रिज्या के '''अनुपात''' के रूप में परिभाषित किया जाता है। | ||
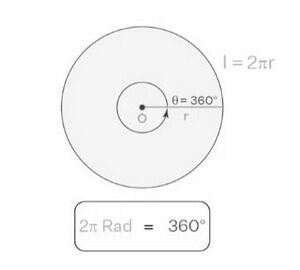
यदि हम चाप को वृत्त की कुल परिधि मानते हैं, तो चाप की लंबाई <math>=2\pi r</math>। साथ ही, हम जानते हैं कि वृत्त की परिधि द्वारा केंद्र पर बनाया गया कोण <math>360^\circ</math> है। फिर उपरोक्त सूत्र से, | यदि हम चाप को वृत्त की कुल परिधि मानते हैं, तो चाप की लंबाई <math>=2\pi r</math>। साथ ही, हम जानते हैं कि वृत्त की परिधि द्वारा केंद्र पर बनाया गया कोण <math>360^\circ</math> है। फिर उपरोक्त सूत्र से, | ||
| Line 32: | Line 35: | ||
<math>360^\circ = 2\pi</math> | <math>360^\circ = 2\pi</math> | ||
[[File:रेडियन सूत्र.jpg|thumb|चित्र-3 रेडियन सूत्र]] | |||
इस प्रकार, रेडियन का सूत्र <math>2\pi=360^\circ</math> है। | इस प्रकार, रेडियन का सूत्र <math>2\pi=360^\circ</math> है। | ||
Latest revision as of 09:00, 13 November 2024
रेडियन एक इकाई है जिसका उपयोग कोणों को मापने के लिए किया जाता है। कोणों को मापने के लिए हमारे पास दो इकाइयाँ हैं: डिग्री और रेडियन। इस चरण तक, आप कोणों के आकार को मापने के लिए डिग्री का उपयोग कर रहे होंगे। हालाँकि, कई कारणों से, उन्नत गणित में कोण माप को प्रायः डिग्री प्रणाली से अलग इकाई प्रणाली का उपयोग करके वर्णित किया जाता है। इस प्रणाली को रेडियन प्रणाली के रूप में जाना जाता है। क्या आप जानते हैं कि 1995 से पहले कोणों को मापने के लिए रेडियन पूरक इकाई थी? बाद में इसे व्युत्पन्न इकाई में बदल दिया गया।
आइए, रेडियन सूत्र, चाप लंबाई सूत्र और कोण को रेडियन से डिग्री और डिग्री से रेडियन में बदलने के तरीके के बारे में विस्तार से जानें।
परिचय
रेडियन एक इकाई है जिसका उपयोग कोणों को मापने के लिए किया जाता है और एक रेडियन एक वृत्त के केंद्र पर एक चाप द्वारा बनाया गया कोण होता है जिसकी लंबाई वृत्त की त्रिज्या के समान होती है। एक रेडियन जो नीचे दिखाया गया है, लगभग डिग्री के समान है। जब हम त्रिज्या के संदर्भ में कोण की गणना करना चाहते हैं तो हम डिग्री के स्थान पर रेडियन का उपयोग करते हैं। जैसे '' का उपयोग डिग्री को दर्शाने के लिए किया जाता है, वैसे ही रेडियन को दर्शाने के लिए या का उपयोग किया जाता है। उदाहरण के लिए, 1.5 रेडियन को 1.5 या 1.5 के रूप में लिखा जाता है।
परिभाषा
"रेडियन" कोण के मापन की एक इकाई है। यहाँ "रेडियन" के बारे में कुछ तथ्य दिए गए हैं
- रेडियन को "" या घातांक में "" चिह्न का उपयोग करके दर्शाया जाता है।
- यदि कोण को बिना किसी इकाई के लिखा जाता है, तो इसका मतलब है कि यह रेडियन में है।
- रेडियन में कोणों के कुछ उदाहरण , , , , आदि हैं।
रेडियन का उपयोग
- कलन(कैलकुलस) और गणित की अधिकांश अन्य शाखाओं में कोणों को ज़्यादातर या साधारणतः रेडियन में मापा जाता है।
- भौतिकी में भी रेडियन का व्यापक रूप से उपयोग किया जाता है। भौतिकी में कोणीय मापन करते समय डिग्री की तुलना में इन्हें प्राथमिकता दी जाती है।
रेडियन सूत्र
हम पहले ही सीख चुके हैं कि रेडियन उस वृत्त के चाप द्वारा बनाए गए कोण के बराबर होता है जिसकी लंबाई वृत्त की त्रिज्या के बराबर होती है। इस प्रकार, एक वृत्त के रेडियन में चाप द्वारा बनाया गया कोण चाप की लंबाई और वृत्त की त्रिज्या के अनुपात के रूप में परिभाषित किया जाता है।
यदि हम चाप को वृत्त की कुल परिधि मानते हैं, तो चाप की लंबाई । साथ ही, हम जानते हैं कि वृत्त की परिधि द्वारा केंद्र पर बनाया गया कोण है। फिर उपरोक्त सूत्र से,
कोण = (चाप की लंबाई)/(त्रिज्या)
इस प्रकार, रेडियन का सूत्र है।
महत्वपूर्ण टिप्पणियाँ:
- हम कोण को डिग्री से रेडियन में से गुणा करके बदल सकते हैं।
- हम कोण को रेडियन से डिग्री में से गुणा करके बदल सकते हैं।
- चाप की लंबाई = त्रिज्या × केंद्र पर अंतरित कोण। इस सूत्र को लागू करते समय, कोण (यदि डिग्री में दिया गया है) को पहले रेडियन में बदलना चाहिए।