डिग्री और रेडियन के बीच संबंध: Difference between revisions

Latest revision as of 10:03, 13 November 2024

परिभाषा

किसी वृत्त की परिधि $=2\pi r$

यदि किसी वृत्त की त्रिज्या $=1$ है तो वृत्त की परिधि $=2\pi$ होगी. इसलिए प्रारंभिक पक्ष की एक पूर्ण परिक्रमण $2\pi$ का कोण अंतरित करती है और इसकी डिग्री माप $360^{\circ }$ होती है ।

$2\pi$ रेडियन $=360^{\circ }$

$\pi$ रेडियन $=180^{\circ }$ $\pi ={\frac {22}{7}}$

चित्र

$1$ रेडियन $={\frac {180^{\circ }}{\pi }}={\frac {180^{\circ }\times 7}{22}}=57^{\circ }16'$ लगभग

$\pi$ रेडियन $=180^{\circ }$ अत: $1^{\circ }={\frac {\pi }{180}}$ रेडियन $={\frac {22}{7\times 180}}=0.01746$ रेडियन लगभग

निम्नलिखित तालिका कुछ सामान्य कोणों की डिग्री माप और रेडियन माप के बीच संबंध को दर्शाती है।

डिग्री	$30^{\circ }$	$45^{\circ }$	$60^{\circ }$	$90^{\circ }$	$180^{\circ }$	$270^{\circ }$	$360^{\circ }$
रेडियन	${\frac {\pi }{6}}$	${\frac {\pi }{4}}$	${\frac {\pi }{3}}$	${\frac {\pi }{2}}$	$\pi$	${\frac {3\pi }{2}}$	$2\pi$

रेडियन माप $={\frac {\pi }{180}}\times$ डिग्री माप

डिग्री माप $={\frac {180}{\pi }}\times$ रेडियन माप

उदाहरण 1

$45^{\circ }20'$ को रेडियन माप में परिवर्तित करें।

रेडियन माप $={\frac {\pi }{180}}\times$ डिग्री माप

$45^{\circ }20'=45{\frac {1}{3}}$ डिग्री $={\frac {136}{3}}$ रेडियन $={\frac {\pi }{180}}\times {\frac {136}{3}}={\frac {34\pi }{135}}\$ रेडियन

अत: $45^{\circ }20'={\frac {34\pi }{135}}\$ रेडियन

उदाहरण 2

$4$ रेडियन को डिग्री माप में परिवर्तित करें।

डिग्री माप $={\frac {180}{\pi }}\times$ रेडियन माप

$={\frac {180}{\pi }}\times 4\$ डिग्री $={\frac {180}{22}}\times 7\times 4={\frac {2520}{11}}=229{\frac {1}{11}}\$ डिग्री

1 डिग्री (1°) = 60 मिनट (60')

$=229\$ डिग्री $+{\frac {1\times 60}{11}}\$ मिनट

$=229\$ डिग्री $+5{\frac {5}{11}}\$ मिनट

1 मिनट(1') = 60 सेकंड (60“)

$=229\$ डिग्री $+5\$ मिनट $+{\frac {5\times 60}{11}}\$ सेकंड

$=229\$ डिग्री $+5\$ मिनट $+27.2\$ सेकंड

अत: $4\$ रेडियन $=229^{\circ }5'27''$ लगभग

रेडियन और डिग्री के बीच रूपांतरण

किसी कोण को "रेडियन से डिग्री" और "डिग्री से रेडियन" में आवश्यकतानुसार परिवर्तित किया जा सकता है। इन रूपांतरणों को करने के लिए हम रेडियन सूत्र (पिछले अनुभाग से), $2\pi =360^{\circ }$ का उपयोग करते हैं। हम नीचे दिए गए चित्र में देख सकते हैं कि रेडियन और डिग्री के बीच रूपांतरण कैसे किया जाता है।

डिग्री को रेडियन में परिवर्तित करना

रेडियन सूत्र इस प्रकार लिखा जा सकता है,

$2\pi$ रेडियन = $360^{\circ }$

इससे, $1$ रेडियन = ${\frac {360^{\circ }}{2\pi }}$ (या)

$1$ रेडियन = ${\frac {180^{\circ }}{\pi }}$

इस प्रकार, रेडियन को डिग्री में बदलने के लिए, हम कोण को ${\frac {180^{\circ }}{\pi }}$ से गुणा करते हैं.

रेडियन को डिग्री में बदलने के उदाहरण:

${\frac {\pi }{2}}={\frac {\pi }{2}}\times {\frac {180^{\circ }}{\pi }}=90^{\circ }$

${\frac {\pi }{4}}={\frac {\pi }{4}}\times {\frac {180^{\circ }}{\pi }}=45^{\circ }$

${\frac {7\pi }{6}}={\frac {7\pi }{6}}\times {\frac {180^{\circ }}{\pi }}=210^{\circ }$

$2$ रेड $=2\times {\frac {180^{\circ }}{\pi }}\approx 114.59^{\circ }$

यदि हम पहले तीन उदाहरणों को देखें, जहाँ कोण $\pi$ के संदर्भ में है, तो इसे डिग्री में बदलने पर $\pi$ रद्द हो रहा है। इसलिए रेडियन में कोण को $\pi$ के संदर्भ में डिग्री में बदलने के लिए, बस $\pi$ को $180^{\circ }$ से बदलें। यह रेडियन को डिग्री में बदलने की एक ट्रिक है। यहाँ आप ट्रिक का उपयोग करके पहले तीन उदाहरण देख सकते हैं।

${\frac {\pi }{2}}={\frac {180^{\circ }}{2}}=90^{\circ }$

${\frac {\pi }{4}}\times {\frac {180^{\circ }}{4}}=45^{\circ }$

${\frac {7\pi }{6}}\times 7{\Bigl (}{\frac {180^{\circ }}{6}}{\Bigr )}=210^{\circ }$

डिग्री को रेडियन में बदलना

रेडियन सूत्र से,

$2\pi$ रेडियन $=360^{\circ }$

इससे, $1^{\circ }={\frac {2\pi }{360}}$ रेडियन

$1^{\circ }={\frac {\pi }{180}}$ रेडियन

इस प्रकार, डिग्री को रेडियन में बदलने के लिए, हम कोण को ${\frac {\pi }{180}}$ रेडियन से गुणा करते हैं।

डिग्री को रेडियन में बदलने के उदाहरण:

$90^{\circ }=90\times {\frac {\pi }{180}}={\frac {\pi }{2}}$

$180^{\circ }=180\times {\frac {\pi }{180}}=\pi$

$210^{\circ }=210\times {\frac {\pi }{180}}={\frac {7\pi }{6}}$

रेडियन और डिग्री तालिका

यहाँ डिग्री में कुछ मानक कोण और रेडियन में संगत कोण वाली एक तालिका दी गई है। यह तालिका रेडियन (या डिग्री) के समतुल्य कोण जानने में सहायक है।


डिग्री	रेडियन
30°	π/6
45°	π/4
60°	π/3
90°	π/2
180°	π
270°	3π/2
360°	2π

रेडियन और डिग्री के बीच अंतर

रेडियन और डिग्री दोनों ही कोणों के माप हैं। रेडियन और डिग्री के बीच कुछ अंतर इस प्रकार हैं।


रेडियन	डिग्री
एक वृत्त जिसकी त्रिज्या 'r' है, की लंबाई 'r' के चाप द्वारा अंतरित कोण को 1 रेडियन के रूप में जाना जाता है।	पूर्ण कोण के 1/360वें भाग को डिग्री कहते हैं।
1 रेडियन को 1^c या कभी-कभी केवल 1 द्वारा दर्शाया जाता है।	1 डिग्री को 1° से दर्शाया जाता है।
किसी कोण को डिग्री से रेडियन में बदलने के लिए उसे π/180 से गुणा करें।	किसी कोण को रेडियन से डिग्री में बदलने के लिए उसे 180/π से गुणा करें।

@@ Line 1: / Line 1: @@
+== परिभाषा ==
+किसी ''वृत्त की परिधि''  <math>=2\pi r</math>
-किसी '''''वृत्त की परिधि'''''  <math>=2\pi r</math>
+यदि किसी ''वृत्त की त्रिज्या''  <math>=1</math> है तो ''वृत्त की परिधि'' <math>=2\pi</math> होगी. इसलिए प्रारंभिक पक्ष की एक पूर्ण परिक्रमण <math>2\pi</math> का [[कोण]] अंतरित करती है और इसकी डिग्री माप <math>
-यदि किसी '''''वृत्त की त्रिज्या'''''  <math>=1</math> है तो '''''वृत्त की परिधि''''' <math>=2\pi</math> होगी. इसलिए प्रारंभिक पक्ष की एक पूर्ण परिक्रमण <math>2\pi</math> का कोण अंतरित करती है और इसकी डिग्री माप <math>
 ^\circ</math> होती है ।
-<math>2\pi</math> '''''रेडियन'''''  <math>= 360^\circ</math>
+<math>2\pi</math> ''रेडियन''  <math>= 360^\circ</math>
-<math>\pi</math> '''''रेडियन'''''  <math>=180^\circ  </math>  <math> \pi = \frac{22}{7} </math>
+<math>\pi</math> ''रेडियन''  <math>=180^\circ  </math>  <math> \pi = \frac{22}{7} </math>
 [[File:Radian.jpg|thumb|चित्र ]]
-<math>1</math> '''''रेडियन'''''   <math>=\frac{180^\circ}{\pi}=\frac{180^\circ \times 7}{22}=57^\circ16' </math> लगभग
+<math>1</math> ''रेडियन''   <math>=\frac{180^\circ}{\pi}=\frac{180^\circ \times 7}{22}=57^\circ16' </math> लगभग
-<math>\pi </math> '''''रेडियन'''''   <math>= 180^\circ  </math> अत:  <math> 1^\circ =\frac{\pi}{180} </math> '''''रेडियन'''''  <math>=\frac{22}{7 \times 180}=0.01746</math> '''''रेडियन'''''  लगभग
+<math>\pi </math> ''रेडियन''   <math>= 180^\circ  </math> अत:  <math> 1^\circ =\frac{\pi}{180} </math> ''रेडियन''  <math>=\frac{22}{7 \times 180}=0.01746</math> ''रेडियन''  लगभग
-निम्नलिखित तालिका कुछ सामान्य कोणों की डिग्री माप और रेडियन माप के बीच संबंध को दर्शाती है।
+निम्नलिखित तालिका कुछ सामान्य कोणों की [[डिग्री माप]] और रेडियन माप के बीच संबंध को दर्शाती है।
 {| class="wikitable"
 |'''''डिग्री'''''
@@ Line 32: / Line 32: @@
 |<math> \frac{3\pi}{2} </math>
 |<math> 2\pi </math>
-|}'''''रेडियन माप'''''  <math>=\frac{\pi}{180} \times </math> '''''डिग्री  माप'''''
+|}''रेडियन माप''  <math>=\frac{\pi}{180} \times </math> ''डिग्री  माप''
-'''''डिग्री'''''  '''''माप'''''  <math>=\frac{180} {\pi}\times</math> '''''रेडियन माप'''''
+''डिग्री''  ''माप''  <math>=\frac{180} {\pi}\times</math> ''रेडियन माप''
 ===उदाहरण 1===
-<math>45^\circ 20'</math> को रेडियन माप में परिवर्तित करें।
+<math>45^\circ 20'</math> को [[रेडियन माप]] में परिवर्तित करें।
-'''''रेडियन माप'''''  <math>=\frac{\pi}{180} \times </math> '''''डिग्री  माप'''''
+''रेडियन माप''  <math>=\frac{\pi}{180} \times </math> ''डिग्री  माप''
-<math>45^\circ 20'=45\frac{1}{3}</math> '''''डिग्री'''''  <math>=\frac{136}{3}</math> '''''रेडियन''''' <math>= \frac{\pi}{180} \times \frac{136}{3}=\frac{34\pi}{135} \ </math>'''''रेडियन'''''
+<math>45^\circ 20'=45\frac{1}{3}</math> ''डिग्री''  <math>=\frac{136}{3}</math> ''रेडियन'' <math>= \frac{\pi}{180} \times \frac{136}{3}=\frac{34\pi}{135} \ </math>''रेडियन''
-अत: <math>45^\circ 20'=\frac{34\pi}{135} \ </math>'''''रेडियन'''''
+अत: <math>45^\circ 20'=\frac{34\pi}{135} \ </math>''रेडियन''
 ===उदाहरण 2===
 <math> 4  </math> रेडियन को डिग्री माप में परिवर्तित करें।
-'''''डिग्री'''''  '''''माप'''''  <math>=\frac{180} {\pi}\times</math> '''''रेडियन माप'''''
+''डिग्री''  ''माप''  <math>=\frac{180} {\pi}\times</math> ''रेडियन माप''
+<math>=\frac{180} {\pi} \times 4 \ </math>''डिग्री''  <math>=\frac{180} {22} \times 7 \times 4 = \frac{2520}{11} =229 \frac{1}{11} \ </math>''डिग्री''
+'''''1''' डिग्री '''(1°) = 60''' मिनट '''(60')'''''
+<math>=229 \ </math>''डिग्री'' <math>+ \frac{1 \times 60}{11} \ </math>''मिनट''
+<math> =229 \ </math>''डिग्री'' <math> + 5\frac{5}{11} \ </math>''मिनट''
+'''''1''' मिनट'''(1') = 60''' सेकंड '''(60“)'''  ''
+<math>=229 \ </math>''डिग्री''  <math> + 5 \ </math>''मिनट''<math> + \frac{5 \times 60}{11} \ </math>''सेकंड''
+<math>=229 \ </math>''डिग्री  '''<math> + 5 \ </math>'''मिनट''<math> + 27.2 \ </math>''सेकंड''
+अत: <math>4 \ </math>''रेडियन''<math> =229^\circ 5'27'' </math>  लगभग
+== रेडियन और डिग्री के बीच रूपांतरण ==
+किसी कोण को "रेडियन से डिग्री" और "डिग्री से रेडियन" में आवश्यकतानुसार परिवर्तित किया जा सकता है। इन रूपांतरणों को करने के लिए हम रेडियन सूत्र (पिछले अनुभाग से),<math>2\pi=360^\circ</math> का उपयोग करते हैं। हम नीचे दिए गए चित्र में देख सकते हैं कि रेडियन और डिग्री के बीच रूपांतरण कैसे किया जाता है।
+== डिग्री को रेडियन में परिवर्तित करना ==
+रेडियन सूत्र इस प्रकार लिखा जा सकता है,
+<math>2\pi</math> रेडियन = <math>360^\circ</math>
+इससे, <math>1</math> रेडियन =  <math>\frac{360^\circ}{2\pi}</math>  (या)
+<math>1</math> रेडियन = <math>\frac{180^\circ}{\pi}</math>
+इस प्रकार, रेडियन को डिग्री में बदलने के लिए, हम कोण को <math>\frac{180^\circ}{\pi}</math> से गुणा करते हैं.
+रेडियन को डिग्री में बदलने के '''उदाहरण''':
+<math>\frac{\pi}{2}=\frac{\pi}{2}\times \frac{180^\circ}{\pi}=90^\circ</math>
-<math>=\frac{180} {\pi} \times 4 \ </math>'''''डिग्री'''''  <math>=\frac{180} {22} \times 7 \times 4 = \frac{2520}{11} =229 \frac{1}{11} \ </math>'''''डिग्री'''''
+<math>\frac{\pi}{4}=\frac{\pi}{4}\times \frac{180^\circ}{\pi}=45^\circ</math>
-'''''1 डिग्री (1°) = 60 मिनट (60')'''''
+<math>{\frac{7\pi}{6}}=\frac{7\pi}{6}\times \frac{180^\circ}{\pi}=210^\circ</math>
-<math>=229 \ </math>'''''डिग्री''''' <math>+ \frac{1 \times 60}{11} \ </math>'''''मिनट'''''
+<math>2</math> रेड  <math>=2\times \frac{180^\circ}{\pi}\approx114.59^\circ </math>
-<math> =229 \ </math>'''''डिग्री''''' <math> + 5\frac{5}{11} \ </math>'''''मिनट'''''
+यदि हम पहले तीन उदाहरणों को देखें, जहाँ कोण <math>\pi </math> के संदर्भ में है, तो इसे डिग्री में बदलने पर <math>\pi </math> रद्द हो रहा है। इसलिए रेडियन में कोण को <math>\pi </math> के संदर्भ में डिग्री में बदलने के लिए, बस <math>\pi </math> को <math>180^\circ </math> से बदलें। यह रेडियन को डिग्री में बदलने की एक ट्रिक है। यहाँ आप ट्रिक का उपयोग करके पहले तीन उदाहरण देख सकते हैं।
-'''''1 मिनट(1') = 60 सेकंड (60“)'''  ''
+<math>\frac{\pi}{2}= \frac{180^\circ}{2}=90^\circ </math>
-<math>=229 \ </math>'''''डिग्री'''''  <math> + 5 \ </math>'''''मिनट'''''<math> + \frac{5 \times 60}{11} \ </math>'''''सेकंड'''''
+<math>\frac{\pi}{4}\times \frac{180^\circ}{4}=45^\circ </math>
-<math>=229 \ </math>'''''डिग्री  <math> + 5 \ </math>मिनट'''''<math> + 27.2 \ </math>'''''सेकंड'''''
+<math>\frac{7\pi}{6}\times 7\Bigl(\frac{180^\circ}{6}\Bigr)=210^\circ </math>
-अत: <math>4 \ </math>'''''रेडियन'''''<math> =229^\circ 5'27'' </math>  लगभग
+डिग्री को रेडियन में बदलना
+रेडियन सूत्र से,
+<math>2\pi </math> रेडियन <math>=360^\circ </math>
+इससे,  <math> 1^\circ =\frac{2\pi}{360} </math> रेडियन
+<math> 1^\circ =\frac{\pi}{180} </math> रेडियन
+इस प्रकार, डिग्री को रेडियन में बदलने के लिए, हम कोण को <math>\frac{\pi}{180} </math> रेडियन से गुणा करते हैं।
+डिग्री को रेडियन में बदलने के उदाहरण:
+<math>90^\circ=90\times \frac{\pi}{180}=\frac{\pi}{2}</math>
+<math>180^\circ=180\times \frac{\pi}{180}=\pi </math>
+<math>210^\circ=210\times \frac{\pi}{180}=\frac{7\pi}{6}</math>
+== रेडियन और डिग्री तालिका ==
+यहाँ डिग्री में कुछ मानक कोण और रेडियन में संगत कोण वाली एक तालिका दी गई है। यह तालिका रेडियन (या डिग्री) के समतुल्य कोण जानने में सहायक है।
+{| class="wikitable"
+|+
+!डिग्री
+!रेडियन
+|-
+|30°
+|π/6
+|-
+|45°
+|π/4
+|-
+|60°
+|π/3
+|-
+|90°
+|π/2
+|-
+|180°
+|π
+|-
+|270°
+|3π/2
+|-
+|360°
+|2π
+|}
+== रेडियन और डिग्री के बीच अंतर ==
+रेडियन और डिग्री दोनों ही कोणों के माप हैं। रेडियन और डिग्री के बीच कुछ अंतर इस प्रकार हैं।
+{| class="wikitable"
+|+
+!रेडियन
+!डिग्री
+|-
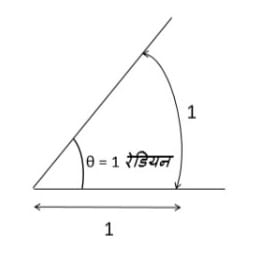
+|एक वृत्त जिसकी त्रिज्या 'r' है, की लंबाई 'r' के चाप द्वारा अंतरित कोण को 1 रेडियन के रूप में जाना जाता है।
+|पूर्ण कोण के 1/360वें भाग को डिग्री कहते हैं।
+|-
+|1 रेडियन को 1<sup>c</sup> या कभी-कभी केवल 1 द्वारा दर्शाया जाता है।
+|1 डिग्री को 1° से दर्शाया जाता है।
+|-
+|किसी कोण को डिग्री से रेडियन में बदलने के लिए उसे π/180 से गुणा करें।
+|किसी कोण को रेडियन से डिग्री में बदलने के लिए उसे 180/π से गुणा करें।
+|}
 [[Category:त्रिकोणमितीय फलन]]
 [[Category:कक्षा-11]]
 [[Category:गणित]]