त्रिकोणमितीय फलनों का चिह्न: Difference between revisions
(added content) |
(added internal links) |
||
| (3 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
[[Category:कक्षा-11]] | [[Category:कक्षा-11]] | ||
[[Category:गणित]] | [[Category:गणित]] | ||
वृत्ताकार फलन, जिन्हें कभी-कभी त्रिकोणमितीय फलन के रूप में भी जाना जाता है, को सरलता से त्रिभुज के कोण के फलन के रूप में वर्णित किया जा सकता है। इसका मतलब है कि ये त्रिकोणमितीय फलन त्रिभुज के कोणों और भुजाओं के बीच संबंध निर्धारित करते हैं। साइन, कोसाइन, टेंगेंट, कोटैंगेंट, सेकेंट और कोसेकेंट मूल त्रिकोणमितीय फलन हैं। कई त्रिकोणमितीय सूत्र और पहचान फलनों के बीच संबंध को परिभाषित करते हैं और त्रिभुज के कोणों के निर्धारण में सहायता करते हैं। | वृत्ताकार फलन, जिन्हें कभी-कभी [[त्रिकोणमितीय फलन]] के रूप में भी जाना जाता है, को सरलता से त्रिभुज के कोण के फलन के रूप में वर्णित किया जा सकता है। इसका मतलब है कि ये त्रिकोणमितीय फलन त्रिभुज के कोणों और भुजाओं के बीच संबंध निर्धारित करते हैं। साइन, कोसाइन, टेंगेंट, कोटैंगेंट, सेकेंट और कोसेकेंट मूल त्रिकोणमितीय फलन हैं। कई त्रिकोणमितीय सूत्र और पहचान फलनों के बीच संबंध को परिभाषित करते हैं और त्रिभुज के कोणों के निर्धारण में सहायता करते हैं। | ||
== छह त्रिकोणमितीय फलन == | == छह त्रिकोणमितीय फलन == | ||
साइन, कोसाइन और स्पर्शज्या कोण त्रिकोणमितीय फलनों के मूलभूत वर्गीकरण हैं। कोटैंजेंट, सेकेंट और कोसेकेंट सभी फलनों को मूल फलनों से निकाला जा सकता है। मूलभूत त्रिकोणमितीय फलनों की तुलना में, अन्य तीन फलनों का | साइन, कोसाइन, और स्पर्शज्या कोण त्रिकोणमितीय फलनों के मूलभूत वर्गीकरण हैं। कोटैंजेंट, सेकेंट और कोसेकेंट सभी फलनों को मूल [[फलनों के प्रकार|फलनों]] से निकाला जा सकता है। मूलभूत त्रिकोणमितीय फलनों की तुलना में, अन्य तीन फलनों का प्रायः उपयोग किया जाता है। इन तीन प्रमुख फलनों की व्याख्या के लिए नीचे दिए गए आरेख पर एक दृष्टि डालें। इस आरेख का नाम साइन-कोस-टैन त्रिभुज है। | ||
'''<math>sin</math> फलन:''' | |||
विपरीत भुजा की लंबाई और कर्ण का अनुपात किसी कोण का sin फलन होता है। जैसा कि आरेख में दिखाया गया है, sin का मान है | |||
<math>sinA=</math> विपरीत/कर्ण | |||
'''<math>cos</math> फलन:''' | |||
कोण का कोसाइन, पड़ोसी भुजा की लंबाई और कर्ण की लंबाई का अनुपात होता है। ऊपर दिए गए चित्र का उपयोग करके cos फलन की गणना की जा सकती है। | |||
<math>cosA=</math> आसन्न/कर्ण | |||
'''<math>tan</math> फलन:''' | |||
स्पर्शरेखा फलन विपरीत भुजा की लंबाई और आसन्न भुजा की लंबाई का अनुपात होता है। यह ध्यान देने योग्य है कि tanको sin और cos के अनुपात के रूप में भी व्यक्त किया जा सकता है। tan फलन इस प्रकार होगा, जैसा कि ऊपर दिए गए आरेख में देखा जा सकता है। | |||
<math>tanA=</math>विपरीत/आसन्न | |||
<math>tan</math> को <math>sin</math> और <math>cos</math> के रूप में भी व्यक्त किया जा सकता है: | |||
<math>tanA = \frac{sinA}{cosA}</math> | |||
सेकेंट, कोसेकेंट और कोटैंजेंट फलन: | |||
तीन पूरक फलन सेकेंट, कोसेकेंट (<math>cosec</math>) और कोटैंजेंट मुख्य फलन <math>sin</math>, <math>cos</math>,और <math>tan</math> से प्राप्त होते हैं। कोसेकेंट (<math>cosec</math>), सेकेंट (<math>sec</math>) और कोटैंजेंट (<math>cot</math>) क्रमशः <math>sin</math>, <math>cos</math>, और <math>tan</math> के पारस्परिक हैं। इनमें से प्रत्येक फलन का सूत्र निम्न है: | |||
<math>secA=\Bigl(\frac{1}{cosA}\Bigr)=</math>कर्ण/आसन्न | |||
<math>cosecA=\Bigl(\frac{1}{sinA}\Bigr)=</math> कर्ण/विपरीत | |||
<math>cotA=\Bigl(\frac{1}{tanA}\Bigr)=</math> आसन्न/विपरीत | |||
[[File:चार चतुर्थांशों में त्रिकोणमितीय फलन.jpg|thumb|चित्र ]] | |||
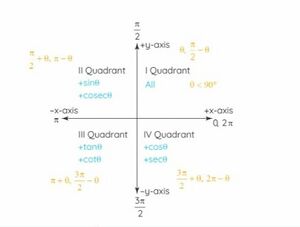
== विभिन्न चतुर्थांशों में त्रिकोणमितीय फ़ंक्शनों के चिह्न == | |||
नीचे दिए गए आरेख में, प्रत्येक चतुर्थांश में त्रिकोणमितीय फलन के चिह्न दिखाए गए हैं। | |||
पहले चतुर्थांश में सभी फलन धनात्मक हैं, | |||
दूसरे चतुर्थांश में केवल <math>sin</math> और <math>cosec</math> धनात्मक हैं, | |||
तीसरे चतुर्थांश में केवल <math>tan</math> और <math>cot</math> धनात्मक हैं, और | |||
चौथे चतुर्थांश में केवल <math>cos</math> और <math>sec</math> धनात्मक हैं। | |||
[[File:त्रिकोणमितीय फलनों का चिह्न.jpg|thumb|चित्र त्रिकोणमितीय फलनों का चिह्न]] | |||
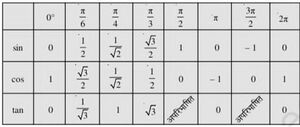
परिणामस्वरूप, विभिन्न चतुर्थांशों में विभिन्न त्रिकोणमितीय फलनों के चिह्नों को निम्नानुसार सारणीबद्ध किया जा सकता है: | |||
'''उदाहरण''' | |||
यदि <math>cot x = \frac{-5}{12}</math> है और <math>x</math> चौथे चतुर्थांश में स्थित है, तो <math>cosecx</math> का मान ज्ञात करें। | |||
'''समाधान''' | |||
दिया गया है, | |||
<math>cot x = \frac{-5}{12}</math> | |||
हम जानते हैं कि, | |||
<math>cosec^2x-cot^2x=1</math> | |||
<math>cosec^2x=1+cot^2x</math> | |||
<math>=1+\Bigl(\frac{-5}{12}\Bigr)^2</math> | |||
<math>=1+\left ( \frac{25}{144} \right )</math> | |||
<math>=\frac{(144+25)}{144}</math> | |||
<math>=\frac{169}{144}</math> | |||
<math>cosecx = \sqrt{\left ( \frac{169}{144} \right )}=\frac{\pm13}{12} </math> | |||
दिया गया है कि <math>x</math> चौथे चतुर्थांश में है और चौथे चतुर्थांश में <math>cosecx</math> ऋणात्मक है। | |||
परिणामस्वरूप, <math>cosecx= \frac{-13}{12}</math> | |||
इसी तरह, हम आसानी से त्रिकोणमिति की कई समस्याओं को हल कर सकते हैं। इनका उपयोग त्रिकोणमिति कार्यों के मानों की गणना करने के लिए किया जा सकता है जो अन्य कार्यों के साथ-साथ त्रिकोणमिति कोणों पर भी निर्भर हैं। | |||
== निष्कर्ष == | |||
त्रिकोणमितीय फलन का चिह्न कोण के टर्मिनल पक्ष पर बिंदुओं के निर्देशांक द्वारा निर्धारित किया जाता है। आप यह जानकर सभी त्रिकोणमितीय फलन के चिह्नों का पता लगा सकते हैं कि कोण का टर्मिनल पक्ष किस चतुर्थांश में है। कोण का टर्मिनल पक्ष आठ स्थानों में से किसी एक में पाया जा सकता है: चार चतुर्थांशों में से किसी एक में, या अक्षों के साथ सकारात्मक या नकारात्मक दिशा में (चतुर्थांश कोण)। त्रिकोणमितीय फलन के चिह्नों के लिए, प्रत्येक परिदृश्य का एक अलग अर्थ होता है। | |||
Latest revision as of 16:10, 13 November 2024
वृत्ताकार फलन, जिन्हें कभी-कभी त्रिकोणमितीय फलन के रूप में भी जाना जाता है, को सरलता से त्रिभुज के कोण के फलन के रूप में वर्णित किया जा सकता है। इसका मतलब है कि ये त्रिकोणमितीय फलन त्रिभुज के कोणों और भुजाओं के बीच संबंध निर्धारित करते हैं। साइन, कोसाइन, टेंगेंट, कोटैंगेंट, सेकेंट और कोसेकेंट मूल त्रिकोणमितीय फलन हैं। कई त्रिकोणमितीय सूत्र और पहचान फलनों के बीच संबंध को परिभाषित करते हैं और त्रिभुज के कोणों के निर्धारण में सहायता करते हैं।
छह त्रिकोणमितीय फलन
साइन, कोसाइन, और स्पर्शज्या कोण त्रिकोणमितीय फलनों के मूलभूत वर्गीकरण हैं। कोटैंजेंट, सेकेंट और कोसेकेंट सभी फलनों को मूल फलनों से निकाला जा सकता है। मूलभूत त्रिकोणमितीय फलनों की तुलना में, अन्य तीन फलनों का प्रायः उपयोग किया जाता है। इन तीन प्रमुख फलनों की व्याख्या के लिए नीचे दिए गए आरेख पर एक दृष्टि डालें। इस आरेख का नाम साइन-कोस-टैन त्रिभुज है।
फलन:
विपरीत भुजा की लंबाई और कर्ण का अनुपात किसी कोण का sin फलन होता है। जैसा कि आरेख में दिखाया गया है, sin का मान है
विपरीत/कर्ण
फलन:
कोण का कोसाइन, पड़ोसी भुजा की लंबाई और कर्ण की लंबाई का अनुपात होता है। ऊपर दिए गए चित्र का उपयोग करके cos फलन की गणना की जा सकती है।
आसन्न/कर्ण
फलन:
स्पर्शरेखा फलन विपरीत भुजा की लंबाई और आसन्न भुजा की लंबाई का अनुपात होता है। यह ध्यान देने योग्य है कि tanको sin और cos के अनुपात के रूप में भी व्यक्त किया जा सकता है। tan फलन इस प्रकार होगा, जैसा कि ऊपर दिए गए आरेख में देखा जा सकता है।
विपरीत/आसन्न
को और के रूप में भी व्यक्त किया जा सकता है:
सेकेंट, कोसेकेंट और कोटैंजेंट फलन:
तीन पूरक फलन सेकेंट, कोसेकेंट () और कोटैंजेंट मुख्य फलन , ,और से प्राप्त होते हैं। कोसेकेंट (), सेकेंट () और कोटैंजेंट () क्रमशः , , और के पारस्परिक हैं। इनमें से प्रत्येक फलन का सूत्र निम्न है:
कर्ण/आसन्न
कर्ण/विपरीत
आसन्न/विपरीत
विभिन्न चतुर्थांशों में त्रिकोणमितीय फ़ंक्शनों के चिह्न
नीचे दिए गए आरेख में, प्रत्येक चतुर्थांश में त्रिकोणमितीय फलन के चिह्न दिखाए गए हैं।
पहले चतुर्थांश में सभी फलन धनात्मक हैं,
दूसरे चतुर्थांश में केवल और धनात्मक हैं,
तीसरे चतुर्थांश में केवल और धनात्मक हैं, और
चौथे चतुर्थांश में केवल और धनात्मक हैं।
परिणामस्वरूप, विभिन्न चतुर्थांशों में विभिन्न त्रिकोणमितीय फलनों के चिह्नों को निम्नानुसार सारणीबद्ध किया जा सकता है:
उदाहरण
यदि है और चौथे चतुर्थांश में स्थित है, तो का मान ज्ञात करें।
समाधान
दिया गया है,
हम जानते हैं कि,
दिया गया है कि चौथे चतुर्थांश में है और चौथे चतुर्थांश में ऋणात्मक है।
परिणामस्वरूप,
इसी तरह, हम आसानी से त्रिकोणमिति की कई समस्याओं को हल कर सकते हैं। इनका उपयोग त्रिकोणमिति कार्यों के मानों की गणना करने के लिए किया जा सकता है जो अन्य कार्यों के साथ-साथ त्रिकोणमिति कोणों पर भी निर्भर हैं।
निष्कर्ष
त्रिकोणमितीय फलन का चिह्न कोण के टर्मिनल पक्ष पर बिंदुओं के निर्देशांक द्वारा निर्धारित किया जाता है। आप यह जानकर सभी त्रिकोणमितीय फलन के चिह्नों का पता लगा सकते हैं कि कोण का टर्मिनल पक्ष किस चतुर्थांश में है। कोण का टर्मिनल पक्ष आठ स्थानों में से किसी एक में पाया जा सकता है: चार चतुर्थांशों में से किसी एक में, या अक्षों के साथ सकारात्मक या नकारात्मक दिशा में (चतुर्थांश कोण)। त्रिकोणमितीय फलन के चिह्नों के लिए, प्रत्येक परिदृश्य का एक अलग अर्थ होता है।