वृत्त: Difference between revisions

Latest revision as of 08:20, 22 November 2024

वृत्त एक द्वि-आयामी संवृत आकृति है जिसमें एक घुमावदार पक्ष होता है जिसके सिरे एक गोल आकार बनाने के लिए मिलते हैं। 'सर्कल' शब्द लैटिन शब्द 'सर्कुलस' से लिया गया है जिसका अर्थ है एक छोटी वलय/ गोला। आइए इस लेख में वृत्त की परिभाषा, वृत्त के सूत्र और वृत्त के विभिन्न भागों के बारे में अधिक जानें।

चित्र- वृत्त

परिभाषा

वृत्त एक द्वि-आयामी आकृति है जो समतल पर एक निश्चित बिंदु (केंद्र) से एक निश्चित दूरी (त्रिज्या) पर स्थित बिंदुओं के समूह द्वारा बनाई जाती है। निश्चित बिंदु को वृत्त का मूल या केंद्र कहा जाता है और मूल बिंदु से बिंदुओं की निश्चित दूरी को त्रिज्या कहा जाता है। वृत्त के मूल भागों, केंद्र, त्रिज्या और वृत्त के व्यास को देखने के लिए निम्नलिखित आकृति को देखें।

चित्र- वृत्त के भाग

वृत्त के भाग

वृत्त के कई भाग होते हैं जिन्हें हमें इसके गुणों को समझने के लिए जानना चाहिए। वृत्त के कुछ महत्वपूर्ण भाग नीचे दिए गए हैं।

परिधि: इसे वृत्त की परिधि भी कहा जाता है और इसे वृत्त की सीमा की लंबाई के रूप में परिभाषित किया जा सकता है।

वृत्त की त्रिज्या: त्रिज्या वृत्त के केंद्र से उसकी सीमा पर किसी भी बिंदु तक की दूरी है। एक वृत्त में अनंत संख्या में त्रिज्याएँ होती हैं।

व्यास: व्यास केंद्र से होकर गुजरने वाली एक सरल रेखा होती है जो वृत्त की सीमा पर दो बिंदुओं को जोड़ती है। हमें ध्यान देना चाहिए कि वृत्त में कई व्यास हो सकते हैं, लेकिन उन्हें:

केंद्र से होकर गुजरना चाहिए।

सीधी रेखाएँ होनी चाहिए।

वृत्त की सीमा को दो अलग-अलग बिंदुओं पर स्पर्श करना चाहिए जो एक दूसरे के विपरीत स्थित हों।

वृत्त की जीवा: जीवा वृत्त की सीमा पर दो अलग-अलग बिंदुओं पर वृत्त को छूने वाला कोई भी रेखाखंड होता है। वृत्त में सबसे लंबी जीवा उसका व्यास होता है जो केंद्र से होकर गुजरता है और उसे दो बराबर भागों में विभाजित करता है।

स्पर्शरेखा: स्पर्शरेखा वह रेखा होती है जो वृत्त को एक अद्वितीय बिंदु पर स्पर्श करती है और वृत्त के बाहर स्थित होती है।

छेदक: वह रेखा जो वृत्त के चाप/परिधि पर दो बिंदुओं को प्रतिच्छेद करती है उसे छेदक कहते हैं।

वृत्त का चाप: वृत्त के चाप को वक्र कहते हैं जो उसकी परिधि का एक भाग या भाग होता है।

वृत्त में खंड: वृत्त में जीवा और संगत चाप द्वारा घेरा गया क्षेत्र खंड कहलाता है। खंड दो प्रकार के होते हैं - लघु खंड और दीर्घ खंड।

वृत्त का त्रिज्यखंड: वृत्त का त्रिज्यखंड, वृत्त में दो त्रिज्याओं और संगत चाप द्वारा घेरे गए क्षेत्र के रूप में परिभाषित किया जाता है। त्रिज्यखंड दो प्रकार के होते हैं - लघु त्रिज्यखंड और दीर्घ त्रिज्यखंड।

नीचे दिए गए चित्र को देखें जिसमें वृत्त के सभी महत्वपूर्ण भाग दर्शाए गए हैं।

चित्र- वृत्त का समीकरण

वृत्त - शंकु के परिच्छेद

वृत्त एक विशेष प्रकार का दीर्घवृत्त है जहाँ काटने वाला तल शंकु के आधार के समानांतर होता है। वृत्त में एक फोकस होता है जिसे वृत्त का केंद्र कहा जाता है। वृत्त पर बिंदुओं का स्थान वृत्त के फोकस या केंद्र से एक निश्चित दूरी पर होता है और इसे वृत्त की त्रिज्या कहा जाता है। वृत्त के लिए उत्केन्द्रता $(e)$ का मान $e=0$ है। वृत्त की कोई नियता नहीं होती। $(h,k)$ पर केंद्र और त्रिज्या $r$ वाले वृत्त के समीकरण का सामान्य रूप:

$(x-h)^{2}+(y-k)^{2}=r^{2}$

वृत्त के गुणधर्म

आइए आगे बढ़ते हैं और वृत्तों के कुछ रोचक गुणों के बारे में सीखते हैं जो उन्हें अन्य ज्यामितीय आकृतियों से अलग बनाते हैं। यहाँ वृत्त के गुणों की एक सूची दी गई है:

वृत्त एक बंद $2D$ आकार है जिसमें एक घुमावदार चेहरा होता है।
दो वृत्तों को समरूप कहा जा सकता है यदि उनकी त्रिज्या समान हो।
समान जीवाएँ हमेशा वृत्त के केंद्र से समान दूरी पर होती हैं।
जीवा का लंबवत द्विभाजक वृत्त के केंद्र से होकर गुजरता है।
जब दो वृत्त प्रतिच्छेद करते हैं, तो प्रतिच्छेद करने वाले बिंदुओं को जोड़ने वाली रेखा उनके केंद्र बिंदुओं को जोड़ने वाली रेखा के लंबवत होगी।
व्यास के अंत बिंदुओं पर खींची गई स्पर्शरेखाएँ एक दूसरे के समानांतर होती हैं।

उदाहरण

उदाहरण 1: यदि किसी वृत्ताकार पूल की त्रिज्या $20$ इकाई है, तो पूल के व्यास की लंबाई क्या है?

समाधान:

दिया गया: त्रिज्या $r=20$ इकाई $\Rightarrow$ पूल (वृत्त) का व्यास $=2\times r$ इसलिए, वृत्ताकार पूल के व्यास की लंबाई $=2\times 20=40$ इकाई।

उदाहरण 2 : एक मेज़पोश(टेबलटॉप) एक वृत्त के आकार का है। यदि मेज़पोश की त्रिज्या $21$ इंच है, तो मेज़पोश का क्षेत्रफल ज्ञात करें।

समाधान:

दिया गया: $r=21$ इंच, $\pi ={\frac {22}{7}}$ । सूत्र का उपयोग करते हुए, क्षेत्रफल $=\pi r^{2}\Rightarrow A={\frac {22}{7}}\times 21\times 21=1386$ वर्ग इंच। इसलिए, मेज़पोश का क्षेत्रफल $1386$ वर्ग इंच है।

@@ Line 1: / Line 1: @@
+[[Category:वृत्त]]
+वृत्त एक द्वि-आयामी संवृत आकृति है जिसमें एक घुमावदार पक्ष होता है जिसके सिरे एक गोल आकार बनाने के लिए मिलते हैं। 'सर्कल' शब्द लैटिन शब्द 'सर्कुलस' से लिया गया है जिसका अर्थ है एक छोटी वलय/ गोला। आइए इस लेख में वृत्त की परिभाषा, वृत्त के सूत्र और वृत्त के विभिन्न भागों के बारे में अधिक जानें।
+[[File:वृत्त.jpg|thumb|240x240px|चित्र- वृत्त]]
+== परिभाषा ==
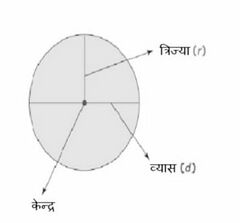
+वृत्त एक द्वि-आयामी आकृति है जो समतल पर एक निश्चित बिंदु (केंद्र) से एक निश्चित दूरी (त्रिज्या) पर स्थित बिंदुओं के समूह द्वारा बनाई जाती है। निश्चित बिंदु को वृत्त का मूल या केंद्र कहा जाता है और मूल बिंदु से बिंदुओं की निश्चित दूरी को त्रिज्या कहा जाता है। वृत्त के मूल भागों, केंद्र, त्रिज्या और वृत्त के व्यास को देखने के लिए निम्नलिखित आकृति को देखें।
+[[File:वृत्त के भाग.jpg|thumb|240x240px|चित्र- वृत्त के भाग]]
+== वृत्त के भाग ==
+वृत्त के कई भाग होते हैं जिन्हें हमें इसके गुणों को समझने के लिए जानना चाहिए। वृत्त के कुछ महत्वपूर्ण भाग नीचे दिए गए हैं।
+'''परिधि''': इसे वृत्त की परिधि भी कहा जाता है और इसे वृत्त की सीमा की लंबाई के रूप में परिभाषित किया जा सकता है।
+'''वृत्त की त्रिज्या''': त्रिज्या वृत्त के केंद्र से उसकी सीमा पर किसी भी बिंदु तक की दूरी है। एक वृत्त में अनंत [[संख्या]] में त्रिज्याएँ होती हैं।
+'''व्यास''': व्यास केंद्र से होकर गुजरने वाली एक सरल रेखा होती है जो वृत्त की सीमा पर दो बिंदुओं को जोड़ती है। हमें ध्यान देना चाहिए कि वृत्त में कई व्यास हो सकते हैं, लेकिन उन्हें:
+केंद्र से होकर गुजरना चाहिए।
+सीधी रेखाएँ होनी चाहिए।
+वृत्त की सीमा को दो अलग-अलग बिंदुओं पर स्पर्श करना चाहिए जो एक दूसरे के विपरीत स्थित हों।
+'''वृत्त की जीवा''': जीवा वृत्त की सीमा पर दो अलग-अलग बिंदुओं पर वृत्त को छूने वाला कोई भी रेखाखंड होता है। वृत्त में सबसे लंबी जीवा उसका व्यास होता है जो केंद्र से होकर गुजरता है और उसे दो बराबर भागों में विभाजित करता है।
+'''स्पर्शरेखा''': स्पर्शरेखा वह रेखा होती है जो वृत्त को एक अद्वितीय बिंदु पर स्पर्श करती है और वृत्त के बाहर स्थित होती है।
+'''छेदक''': वह रेखा जो वृत्त के चाप/परिधि पर दो बिंदुओं को प्रतिच्छेद करती है उसे छेदक कहते हैं।
+'''वृत्त का चाप''': वृत्त के चाप को वक्र कहते हैं जो उसकी परिधि का एक भाग या भाग होता है।
+'''वृत्त में खंड''': वृत्त में जीवा और संगत चाप द्वारा घेरा गया क्षेत्र खंड कहलाता है। खंड दो प्रकार के होते हैं - लघु खंड और दीर्घ खंड।
+'''वृत्त का त्रिज्यखंड''': वृत्त का त्रिज्यखंड, वृत्त में दो त्रिज्याओं और संगत चाप द्वारा घेरे गए क्षेत्र के रूप में परिभाषित किया जाता है। त्रिज्यखंड दो प्रकार के होते हैं - लघु त्रिज्यखंड और दीर्घ त्रिज्यखंड।
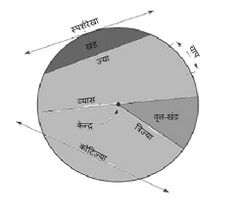
+नीचे दिए गए चित्र को देखें जिसमें वृत्त के सभी महत्वपूर्ण भाग दर्शाए गए हैं।
+[[File:वृत्त का समीकरण.jpg|thumb|235x235px|चित्र- वृत्त का समीकरण]]
+== वृत्त - [[शंकु के परिच्छेद]] ==
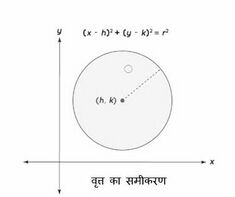
+वृत्त एक विशेष प्रकार का दीर्घवृत्त है जहाँ काटने वाला तल शंकु के आधार के समानांतर होता है। वृत्त में एक फोकस होता है जिसे वृत्त का केंद्र कहा जाता है। वृत्त पर बिंदुओं का स्थान वृत्त के फोकस या केंद्र से एक निश्चित दूरी पर होता है और इसे वृत्त की त्रिज्या कहा जाता है। वृत्त के लिए उत्केन्द्रता <math>(e)</math> का मान <math>e = 0</math> है। वृत्त की कोई नियता नहीं होती। <math>(h, k)</math> पर केंद्र और त्रिज्या <math>r</math> वाले वृत्त के समीकरण का सामान्य रूप:
+<math>(x-h)^2 + (y-k)^2 = r^2</math>
+== वृत्त के गुणधर्म ==
+आइए आगे बढ़ते हैं और वृत्तों के कुछ रोचक गुणों के बारे में सीखते हैं जो उन्हें अन्य ज्यामितीय आकृतियों से अलग बनाते हैं। यहाँ वृत्त के गुणों की एक सूची दी गई है:
+* वृत्त एक बंद <math>2D</math>आकार है जिसमें एक घुमावदार चेहरा होता है।
+* दो वृत्तों को समरूप कहा जा सकता है यदि उनकी त्रिज्या समान हो।
+* समान जीवाएँ हमेशा वृत्त के केंद्र से समान दूरी पर होती हैं।
+* जीवा का लंबवत द्विभाजक वृत्त के केंद्र से होकर गुजरता है।
+* जब दो वृत्त प्रतिच्छेद करते हैं, तो प्रतिच्छेद करने वाले बिंदुओं को जोड़ने वाली रेखा उनके केंद्र बिंदुओं को जोड़ने वाली रेखा के लंबवत होगी।
+* व्यास के अंत बिंदुओं पर खींची गई स्पर्शरेखाएँ एक दूसरे के समानांतर होती हैं।
+== उदाहरण ==
+'''उदाहरण 1''': यदि किसी वृत्ताकार पूल की त्रिज्या <math>20</math> इकाई है, तो पूल के व्यास की लंबाई क्या है?
+'''समाधान''':
+दिया गया: त्रिज्या<math>r = 20</math> इकाई <math> \Rightarrow</math> पूल (वृत्त) का व्यास <math>= 2 \times r</math> इसलिए, वृत्ताकार पूल के व्यास की लंबाई<math>= 2 \times 20 = 40</math>इकाई।
+'''उदाहरण 2''' : एक मेज़पोश(टेबलटॉप) एक वृत्त के आकार का है। यदि मेज़पोश की त्रिज्या <math>21</math> इंच है, तो मेज़पोश का क्षेत्रफल ज्ञात करें।
+'''समाधान''':
+दिया गया: <math>r = 21</math> इंच, <math>\pi = \frac{22 }{7 }</math>।  सूत्र का उपयोग करते हुए, क्षेत्रफल <math>= \pi r^2 \Rightarrow A = \frac{22}{7} \times 21 \times 21 = 1386</math> वर्ग इंच। इसलिए, मेज़पोश का क्षेत्रफल <math>1386</math> वर्ग इंच है।
 [[Category:गणित]]
-[[Category:ज्यामिति]]
+[[Category:गणित]]
-[[Category:वृत्त]]
+[[Category:कक्षा-11]]
-Circle[[Category: कक्षा-11]][[Category: कक्षा -9]]