उत्केन्द्रता: Difference between revisions

Latest revision as of 08:21, 23 November 2024

किसी भी वक्र आकार की उत्केन्द्रता उसके आकार को दर्शाती है, चाहे उसका आकार कुछ भी हो। जब कोई समतल दोहरे शंकु से प्रतिच्छेद करता है तो बनने वाले चार वक्र वृत्त, दीर्घवृत्त, परवलय और अतिपरवलय होते हैं। उनकी विशेषताओं को उनके आकार के आधार पर वर्गीकृत किया जाता है जो उत्केन्द्रता नामक एक प्रभावशाली कारक द्वारा निर्धारित होते हैं। वृत्तों में शून्य उत्केन्द्रता होती है और परवलय में इकाई उत्केन्द्रता होती है। दीर्घवृत्त और अतिपरवलय में अलग-अलग उत्केन्द्रताएँ होती हैं। आइए शंकु वर्गों की उत्केन्द्रता की गणना के बारे में अधिक विस्तार से जानें।

चित्र- शंकु परिच्छेद की उत्केन्द्रता

परिभाषा

शंकु वर्गों की उत्केन्द्रता को शंकु वर्ग पर किसी भी बिंदु से नाभि तक की दूरी और उस बिंदु से निकटतम नियता तक लंबवत दूरी के अनुपात के रूप में परिभाषित किया जाता है। किसी भी शंकु वर्ग के लिए, शंकु वर्ग की उत्केन्द्रता वक्र पर किसी भी बिंदु की उसके नाभि से दूरी $\div$ उसी बिंदु की उसकी नियता से दूरी $=$ एक स्थिरांक है। इस स्थिरांक मान को उत्केन्द्रता के रूप में जाना जाता है, जिसे $e$ द्वारा दर्शाया जाता है। एक वक्र आकार की उत्केन्द्रता यह निर्धारित करती है कि आकार कितना गोल है। उत्केन्द्रता बढ़ने पर वक्रता कम हो जाती है।

यदि उत्केन्द्रताएँ बड़ी हैं, तो वक्र कम होंगे। इस प्रकार हम निष्कर्ष निकालते हैं कि इन शंकु वर्गों की वक्रताएँ उनकी उत्केन्द्रता बढ़ने के साथ घटती हैं।

एक वृत्त की उत्केन्द्रता $=0$

एक दीर्घवृत्त की उत्केन्द्रता $=0$ और $1$ के बीच

एक परवलय की उत्केन्द्रता $=1$

एक अतिपरवलय की उत्केन्द्रता $>1$

एक रेखा की उत्केन्द्रता $=$ अनंत

उत्केन्द्रता सूत्र

ग्रह पृथ्वी के चारों ओर दीर्घवृत्ताकार कक्षा में घूमते हैं। पृथ्वी की कक्षा की उत्केन्द्रता ( $e=0.0167$ ) मंगल की कक्षा ( $e=0.0935$ ) की तुलना में कम है। उत्केन्द्रता का मान शून्य से जितना दूर होता जाता है, आकार उतना ही कम वृत्त जैसा दिखाई देता है। जबकि एक दीर्घवृत्त और एक अतिपरवलय में दो नाभियाँ और दो नियताएँ होती हैं, एक परवलय में एक नाभि और एक नियता होती है। उनके उत्केन्द्रता सूत्र उनके अर्ध-दीर्घ अक्ष ( $a$ ) और अर्ध-लघु अक्ष ( $b$ ) के संदर्भ में दिए गए हैं, दीर्घवृत्त के मामले में और $a=$ अर्ध-अनुप्रस्थ अक्ष और $b=$ अर्ध-संयुग्मी अक्ष अतिपरवलय के स्थिति में। उत्केन्द्रता का सूत्र इस प्रकार दिया गया है

उत्केन्द्रता = नाभि से दूरी/ नियता से दूरी ।

$e={\frac {c}{a}}$

जहाँ,

$e=$ उत्केन्द्रता

$c=$ शंकु खंड पर किसी भी बिंदु से उसके नाभि तक की दूरी

$a=$ शंकु खंड पर किसी भी बिंदु से उसके नियता तक की दूरी

दीर्घवृत्त की उत्केन्द्रता

दीर्घवृत्त एक समतल में सभी बिंदुओं का समूह है, जहाँ समतल में दो निश्चित बिंदुओं (फोकी) से दूरियों का योग स्थिर होता है। दीर्घवृत्त की उत्केन्द्रता उसके केंद्र से उसके किसी भी नाभि और उसके किसी एक शीर्ष से दूरी का अनुपात है। $e={\frac {c}{a}}$ ।

हम जानते हैं कि $c={\sqrt {a^{2}-b^{2}}}$

यदि $a>b,e={\frac {\sqrt {a^{2}-b^{2}}}{a}}$

यदि $a<b,e={\frac {\sqrt {b^{2}-a^{2}}}{b}}$

जहाँ $a=$ अर्ध-प्रमुख अक्ष

$b=$ अर्ध-लघु अक्ष और

$c=$ दीर्घवृत्त के केंद्र से किसी भी नाभि की दूरी।

दीर्घवृत्त की उत्केन्द्रता $0\leq e<1$ है।

वृत्त की उत्केन्द्रता

समतल में सभी बिंदुओं का समूह जो समतल में एक निश्चित बिंदु (केंद्र) से समान दूरी पर होते हैं, वृत्त कहलाता है। वृत्त एक दीर्घवृत्त होता है जिसमें दोनों नाभियाँ उसके केंद्र के साथ मिलती हैं। चूँकि नाभियाँ एक ही बिंदु पर होती हैं, इसलिए वृत्त के लिए केंद्र से नाभि की दूरी शून्य होती है। यह उत्केन्द्रता वृत्त को उसका गोल आकार देती है। इस प्रकार किसी भी वृत्त की उत्केन्द्रता $0$ होती है।

परवलय की उत्केन्द्रता

परवलय एक समतल में सभी बिंदुओं का समूह है जो एक निश्चित रेखा जिसे डायरेक्ट्रिक्स कहते हैं और एक निश्चित बिंदु जिसे नाभि कहते हैं, से समान दूरी पर होते हैं। गतिमान बिंदु $P$ का स्थान परवलय बनाता है, जो तब होता है जब उत्केन्द्रता $e=1$ होती है। यह परवलय वक्र को $\bigcup$ आकार देता है। इस प्रकार परवलय की उत्केन्द्रता सदैव $1$ होती है।

अतिपरवलय की उत्केन्द्रता

अतिपरवलय उन सभी बिंदुओं का समूह है, जिनकी समतल में दो निश्चित बिंदुओं (नाभि ) से दूरियों का अंतर एक स्थिरांक होता है। अतिपरवलय में, $2a$ अनुप्रस्थ अक्ष की लंबाई है और $2b$ संयुग्मी अक्ष की लंबाई है। दो नाभियों के बीच की दूरी $2c$ है। दीर्घवृत्त के समान, अतिपरवलय में एक उत्केन्द्रता होती है जो $c$ और $a$ का अनुपात होती है। चूँकि $c\geq a$ , इसलिए उत्केन्द्रता कभी भी $1$ से कम नहीं होती है। अतिपरवलय की उत्केन्द्रता $e={\frac {\sqrt {a^{2}+b^{2}}}{a}}$ द्वारा दी जाती है। दो नाभियों के बीच की दूरी $=2ae$ ।

महत्वपूर्ण टिप्पणियाँ

शंकु वर्गों की उत्केन्द्रता उनकी वक्रता निर्धारित करती है।
वृत्त की उत्केन्द्रता $0$ होती है और परवलय की उत्केन्द्रता $1$ होती है।
दीर्घवृत्त और परवलय की बदलती उत्केन्द्रता की गणना सूत्र $e={\frac {c}{a}}$ का उपयोग करके की जाती है, जहाँ $c={\sqrt {a^{2}+b^{2}}}$ , जहाँ $a$ और $b$ हाइपरबोला के लिए अर्ध-अक्ष हैं और दीर्घवृत्त के स्थिति में $c={\sqrt {a^{2}-b^{2}}}$ है।

@@ Line 1: / Line 1: @@
-Eccentricity
+किसी भी वक्र आकार की उत्केन्द्रता उसके आकार को दर्शाती है, चाहे उसका आकार कुछ भी हो। जब कोई समतल दोहरे [[शंकु के परिच्छेद|शंकु से प्रतिच्छेद]] करता है तो बनने वाले चार वक्र वृत्त, दीर्घवृत्त, परवलय और अतिपरवलय होते हैं। उनकी विशेषताओं को उनके आकार के आधार पर वर्गीकृत किया जाता है जो उत्केन्द्रता नामक एक प्रभावशाली कारक द्वारा निर्धारित होते हैं। वृत्तों में शून्य उत्केन्द्रता होती है और परवलय में इकाई उत्केन्द्रता होती है। दीर्घवृत्त और अतिपरवलय में अलग-अलग उत्केन्द्रताएँ होती हैं। आइए शंकु वर्गों की उत्केन्द्रता की गणना के बारे में अधिक विस्तार से जानें।
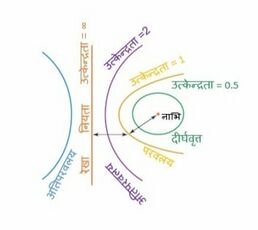
+[[File:शंकु परिच्छेद की उत्केन्द्रता.jpg|thumb|258x258px|चित्र- शंकु परिच्छेद की उत्केन्द्रता]]
+== परिभाषा ==
+शंकु वर्गों की उत्केन्द्रता को शंकु वर्ग पर किसी भी बिंदु से नाभि तक की दूरी और उस बिंदु से निकटतम नियता तक लंबवत दूरी के अनुपात के रूप में परिभाषित किया जाता है। किसी भी शंकु वर्ग के लिए, शंकु वर्ग की उत्केन्द्रता वक्र पर किसी भी बिंदु की उसके नाभि से दूरी <math>\div</math> उसी बिंदु की उसकी नियता से दूरी <math>=</math> एक स्थिरांक है। इस स्थिरांक मान को उत्केन्द्रता के रूप में जाना जाता है, जिसे <math>e </math> द्वारा दर्शाया जाता है। एक वक्र आकार की उत्केन्द्रता यह निर्धारित करती है कि आकार कितना गोल है। उत्केन्द्रता बढ़ने पर वक्रता कम हो जाती है।
+यदि उत्केन्द्रताएँ बड़ी हैं, तो वक्र कम होंगे। इस प्रकार हम निष्कर्ष निकालते हैं कि इन शंकु वर्गों की वक्रताएँ उनकी उत्केन्द्रता बढ़ने के साथ घटती हैं।
+एक [[वृत्त]] की उत्केन्द्रता <math>=0 </math>
+एक [[दीर्घवृत्त]] की उत्केन्द्रता <math>=0 </math> और <math>1 </math> के बीच
+एक परवलय की उत्केन्द्रता <math>=1  </math>
+एक अतिपरवलय की उत्केन्द्रता <math>> 1 </math>
+एक [[रेखा]] की उत्केन्द्रता <math>=</math> अनंत
+== उत्केन्द्रता सूत्र ==
+ग्रह पृथ्वी के चारों ओर दीर्घवृत्ताकार कक्षा में घूमते हैं। पृथ्वी की कक्षा की उत्केन्द्रता (<math>e = 0.0167 </math>) मंगल की कक्षा (<math>e = 0.0935 </math>) की तुलना में कम है। उत्केन्द्रता का मान शून्य से जितना दूर होता जाता है, आकार उतना ही कम वृत्त जैसा दिखाई देता है। जबकि एक दीर्घवृत्त और एक अतिपरवलय में दो नाभियाँ और दो नियताएँ होती हैं, एक परवलय में एक नाभि और एक नियता होती है। उनके उत्केन्द्रता सूत्र उनके अर्ध-दीर्घ अक्ष  (<math>a  </math>) और अर्ध-लघु अक्ष (<math>b </math>) के संदर्भ में दिए गए हैं, दीर्घवृत्त के मामले में और <math>a= </math>अर्ध-अनुप्रस्थ अक्ष और <math>b  = </math> अर्ध-संयुग्मी अक्ष अतिपरवलय के स्थिति में। उत्केन्द्रता का सूत्र इस प्रकार दिया गया है
+उत्केन्द्रता = नाभि से दूरी/ नियता से दूरी ।
+<math>e =\frac{c }{a } </math>
+जहाँ,
+<math>e= </math>  उत्केन्द्रता
+<math>c = </math> शंकु खंड पर किसी भी बिंदु से उसके नाभि तक की दूरी
+<math>a= </math> शंकु खंड पर किसी भी बिंदु से उसके नियता तक की दूरी
+== दीर्घवृत्त की उत्केन्द्रता ==
+दीर्घवृत्त एक समतल में सभी बिंदुओं का समूह है, जहाँ समतल में दो निश्चित बिंदुओं (फोकी) से दूरियों का योग स्थिर होता है। दीर्घवृत्त की उत्केन्द्रता उसके केंद्र से उसके किसी भी नाभि और उसके किसी एक शीर्ष से दूरी का अनुपात है। <math>e =\frac{c }{a } </math> ।
+हम जानते हैं कि  <math>c = \sqrt{a^2-b^2} </math>
+यदि <math>a > b, e = \frac{\sqrt{a^2-b^2} }{a} </math>
+यदि <math>a < b, e = \frac{\sqrt{b^2-a^2} }{b} </math>
+जहाँ <math>a= </math> अर्ध-प्रमुख अक्ष
+<math>b  = </math> अर्ध-लघु अक्ष और
+<math>c = </math> दीर्घवृत्त के केंद्र से किसी भी नाभि की दूरी।
+दीर्घवृत्त की उत्केन्द्रता <math>0 \leq e< 1 </math> है।
+== वृत्त की उत्केन्द्रता ==
+समतल में सभी बिंदुओं का समूह जो समतल में एक निश्चित बिंदु (केंद्र) से समान दूरी पर होते हैं, वृत्त कहलाता है। वृत्त एक दीर्घवृत्त होता है जिसमें दोनों नाभियाँ उसके केंद्र के साथ मिलती हैं। चूँकि नाभियाँ एक ही बिंदु पर होती हैं, इसलिए वृत्त के लिए केंद्र से नाभि की दूरी शून्य होती है। यह उत्केन्द्रता वृत्त को उसका गोल आकार देती है। इस प्रकार किसी भी वृत्त की उत्केन्द्रता <math>0 </math> होती है।
+== परवलय की उत्केन्द्रता ==
+परवलय एक समतल में सभी बिंदुओं का समूह है जो एक निश्चित रेखा जिसे डायरेक्ट्रिक्स कहते हैं और एक निश्चित बिंदु जिसे नाभि कहते हैं, से समान दूरी पर होते हैं। गतिमान बिंदु <math>P </math> का स्थान परवलय बनाता है, जो तब होता है जब उत्केन्द्रता <math>e = 1 </math> होती है। यह परवलय वक्र को <math>\bigcup </math> आकार देता है। इस प्रकार परवलय की उत्केन्द्रता सदैव <math>1 </math> होती है।
+== अतिपरवलय की उत्केन्द्रता ==
+[[अतिपरवलय]] उन सभी बिंदुओं का समूह है, जिनकी समतल में दो निश्चित बिंदुओं (नाभि ) से दूरियों का अंतर एक स्थिरांक होता है। अतिपरवलय में, <math>2a  </math> अनुप्रस्थ अक्ष की लंबाई है और <math>2b </math> संयुग्मी अक्ष की लंबाई है। दो नाभियों के बीच की दूरी <math>2c </math> है। दीर्घवृत्त के समान, अतिपरवलय में एक उत्केन्द्रता होती है जो <math>c </math> और <math>a </math> का अनुपात होती है। चूँकि <math>c \geq a </math>, इसलिए उत्केन्द्रता कभी भी <math>1 </math> से कम नहीं होती है। अतिपरवलय की उत्केन्द्रता  <math>e = \frac{\sqrt{a^2+b^2} }{a}  </math> द्वारा दी जाती है। दो नाभियों के बीच की दूरी <math>= 2ae </math>।
+== महत्वपूर्ण टिप्पणियाँ ==
+* शंकु वर्गों की उत्केन्द्रता उनकी वक्रता निर्धारित करती है।
+* वृत्त की उत्केन्द्रता <math>0 </math> होती है और परवलय की उत्केन्द्रता <math>1 </math> होती है।
+* दीर्घवृत्त और परवलय की बदलती उत्केन्द्रता की गणना सूत्र <math>e =\frac{c }{a } </math> का उपयोग करके की जाती है, जहाँ <math>c = \sqrt{a^2+b^2} </math>, जहाँ <math>a </math> और <math>b  </math>हाइपरबोला के लिए अर्ध-अक्ष हैं और दीर्घवृत्त के स्थिति में <math>c = \sqrt{a^2-b^2} </math> है।
+[[Category:शंकु परिच्छेद]]
 [[Category:गणित]]
-[[Category:ज्यामिति]]
+[[Category:कक्षा-11]]