बारंबारता बंटनों का विश्लेषण: Difference between revisions
(added content) |
No edit summary |
||
| (3 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
बारंबारता बंटन, दोहराई गई वस्तुओं की बारंबारता को आलेखी रूप या सारणीबद्ध रूप में दर्शाता है। यह वस्तुओं की बारंबारता का एक दृश्य प्रदर्शन देता है या दिखाता है कि वे कितनी बार घटित हुई हैं। आइए इस लेख में [[बारंबारता बंटन सारणी|बारंबारता बंटन]] के बारे में विस्तार से जानें। | |||
एकत्रित आंकड़ों को तालिका के रूप में व्यवस्थित करने के लिए | == परिचय == | ||
एकत्रित आंकड़ों को तालिका के रूप में व्यवस्थित करने के लिए बारंबारता बंटन का उपयोग किया जाता है। आंकडें, छात्रों द्वारा प्राप्त अंक, विभिन्न शहरों के तापमान, वॉलीबॉल मैच में प्राप्त अंक आदि हो सकते हैं। [[आंकड़ों का आलेखीय निरूपण|आंकड़ों]] के संग्रह के बाद, हमें बेहतर समझ के लिए आंकड़ों को सार्थक तरीके से दिखाना होगा। आंकड़ों को इस तरह से व्यवस्थित करें कि इसकी सभी विशेषताएँ एक तालिका में संक्षेपित हो जाएँ। इसे बारंबारता बंटन के रूप में जाना जाता है। | |||
इसे बेहतर ढंग से समझने के लिए आइए एक उदाहरण पर विचार करें। श्री | इसे बेहतर ढंग से समझने के लिए आइए एक उदाहरण पर विचार करें। | ||
श्री शर्मा जी द्वारा जारी जी.के. प्रश्नोत्तरी में 10 छात्रों के अंक निम्नलिखित हैं <math>15, 17, 20, 15, 20, 17, 17, 14, 14, 20</math>। आइए इस आंकड़ों को बारंबारता बंटन में दर्शाते हैं और उन छात्रों की संख्या ज्ञात क हैं जिन्हें समान अंक मिले हैं। | |||
{| class="wikitable" | {| class="wikitable" | ||
! | !प्रश्नोत्तरी अंक | ||
! | !छात्रों की संख्या | ||
|- | |- | ||
|15 | |15 | ||
| Line 20: | Line 23: | ||
|2 | |2 | ||
|} | |} | ||
हम देख सकते हैं कि एकत्रित सभी | हम देख सकते हैं कि एकत्रित सभी आंकड़ों को प्रश्नोत्तरी अंक और छात्रों की संख्या के स्तंभ के अंतर्गत व्यवस्थित किया गया है। इससे दी गई जानकारी को समझना आसान हो जाता है और हम देख सकते हैं कि समान अंक प्राप्त करने वाले छात्रों की संख्या कितनी है। इस प्रकार, सांख्यिकी में बारंबारता बंटन हमें आंकड़ों को एक दृष्टि में इसकी विशेषताओं को समझने के लिए आसान तरीके से व्यवस्थित करने में मदद करता है। | ||
== बारंबारता बंटन आलेख == | |||
आंकड़ों को आलेख के रूप में दिखाने का एक और उपाय है और इसे बारंबारता बंटन आलेख का उपयोग करके किया जा सकता है। आलेख हमें एकत्रित आंकड़ों को आसान तरीके से समझने में सहायता करते हैं। बारंबारता बंटन का आलेखी प्रतिनिधित्व निम्नलिखित का उपयोग करके दिखाया जा सकता है: | |||
* '''दंड आरेख'''('''बार ग्राफ)''': दंड आरेख आयताकार दंडों के बीच समान दूरी के साथ समान चौड़ाई के आयताकार दंडों का उपयोग करके आंकड़ों का प्रतिनिधित्व करते हैं। | |||
* '''आयतचित्र'''('''हिस्टोग्राम)''': आयतचित्र विभिन्न ऊंचाइयों के आयताकार दंडों का उपयोग करके आंकड़ों की एक आलेखी प्रस्तुति है। आयतचित्र में, आयताकार दंडों के बीच कोई जगह नहीं होती है। | |||
* '''पाइ रेखाचित्र(पाई चार्ट)''': पाइ रेखाचित्र एक प्रकार का आलेख है जो आंकड़ों को एक गोलाकार(वृत) चार्ट में प्रदर्शित करता है। यह आंकड़ों को एक गोलाकार तरीके से अभिलेख करता है और फिर इसे आगे वृतखंडों(सेक्टरों) में विभाजित किया जाता है जो पूरे भागों में से आंकड़ों का एक विशेष भाग दिखाते हैं। | |||
* '''बारंबारता बहुभुज''': आयतचित्र में दंडों के मध्य-बिंदुओं को जोड़कर एक बारंबारता बहुभुज बनाया जाता है। | |||
== बारंबारता बंटन के प्रकार == | |||
सांख्यिकी के अंतर्गत बारंबारता बंटन के चार प्रकार हैं, जिन्हें नीचे समझाया गया है: | |||
'''अवर्गीकृत बारंबारता बंटन''' : यह आंकड़ों मानों के समूहों के बजाय प्रत्येक अलग-अलग आंकड़ों मान में किसी वस्तु(आइटम) की बारंबारता दिखाता है। | |||
'''वर्गीकृत बारंबारता बंटन''' : इस प्रकार में, आंकड़ों को व्यवस्थित किया जाता है और उन्हें वर्ग अंतराल नामक समूहों में विभाजित किया जाता है। प्रत्येक वर्ग अंतराल से संबंधित आंकड़ों की बारंबारता को बारंबारता बंटन तालिका में अभिलेख किया जाता है। वर्गीकृत बारंबारता तालिका वर्ग अंतराल में आवृत्तियों के बंटन को दर्शाती है। | |||
'''सापेक्ष बारंबारता बंटन''' : यह प्रत्येक श्रेणी से जुड़े कुल प्रेक्षणों की संख्या के अनुपात को बताता है। | |||
'''संचयी बारंबारता बंटन''' : यह बारंबारता बंटन में पहली बारंबारता और उसके नीचे की सभी बारंबारता का योग है। आपको अगले मान के साथ एक मान जोड़ना होगा फिर अगले मान के साथ योग को फिर से जोड़ना होगा और इसी तरह अंतिम तक करना होगा। अंतिम संचयी बारंबारता सभी बारंबारता का कुल योग होगी। | |||
== बारंबारता बंटन तालिका == | |||
बारंबारता बंटन तालिका एक चार्ट है जो आंकड़ों के समुच्चय में प्रत्येक वस्तु की बारंबारता को दर्शाता है। आइए मिलान चिन्ह का उपयोग करके बारंबारता बंटन तालिका बनाने के तरीके को समझने के लिए एक उदाहरण पर विचार करें। | |||
[[File:बारंबारता बंटन तालिका.jpg|alt=बारंबारता बंटन तालिका|thumb|चित्र- बारंबारता बंटन तालिका]] | |||
एक कलश जिसमें विभिन्न रंगों के मोती हैं- लाल, हरा, नीला, काला, लाल, हरा, नीला, पीला, लाल, लाल, हरा, हरा, हरा, पीला, लाल, हरा, पीला। प्रत्येक विशेष रंग के मोतियों की सही संख्या जानने के लिए, हमें मोतियों को श्रेणियों में वर्गीकृत करना होगा। प्रत्येक रंग के मोतियों की संख्या का पता लगाने का एक आसान उपाय मिलान चिन्ह का उपयोग करना है। मोतियों को एक-एक करके चुनें और संबंधित पंक्ति और स्तम्भ में मिलान चिन्ह दर्ज करें। फिर, तालिका में प्रत्येक वस्तु के लिए बारंबारता इंगित करें। | |||
इस प्रकार, प्राप्त तालिका को बारंबारता बंटनतालिका कहा जाता है। | |||
== बारंबारता बंटन तालिका के प्रकार == | |||
बारंबारता बंटन तालिकाएँ दो प्रकार की होती हैं: वर्गीकृत और अवर्गीकृत बारंबारता बंटनता लिकाएँ। | |||
'''वर्गीकृत बारंबारता बंटन तालिका''': बड़ी संख्या में प्रेक्षणों या आंकड़ों को व्यवस्थित करने के लिए, हम वर्गीकृत बारंबारता बंटन तालिका का उपयोग करते हैं। इसमें, हम उस विशेष वर्ग अंतराल से संबंधित आंकड़ों की बारंबारता का मिलान करने के लिए वर्ग अंतराल बनाते हैं। | |||
उदाहरण के लिए, टेस्ट में 20 छात्रों द्वारा प्राप्त अंक इस प्रकार हैं। 5, 10, 20, 15, 5, 20, 20, 15, 15, 15, 10, 10, 10, 20, 15, 5, 18, 18, 18, 18 | '''उदाहरण''' के लिए, टेस्ट में 20 छात्रों द्वारा प्राप्त अंक इस प्रकार हैं।<math>5, 10, 20, 15, 5, 20, 20, 15, 15, 15, 10, 10, 10, 20, 15, 5, 18, 18, 18, 18</math> । वर्गीकृत तालिका में आंकड़ों को व्यवस्थित करने के लिए हमें [[वर्ग-अंतराल|वर्ग अंतराल]] बनाने होंगे। इस प्रकार, हम <math>0 - 5, 6 - 10,</math> और इसी तरह के अंकों के वर्ग अंतराल बनाएंगे। नीचे दी गई तालिका में दो स्तम्भ दिखाए गए हैं, एक वर्ग अंतराल (परीक्षण में प्राप्त अंक) का है और दूसरा बारंबारता (छात्रों की संख्या) का है। इसमें हमने मिलान चिन्ह का उपयोग नहीं किया है क्योंकि हमने अंकों की सीधे गणना की है। | ||
{| class="wikitable" | {| class="wikitable" | ||
! | !परीक्षण में प्राप्त अंक(वर्ग अंतराल) | ||
! | !छात्रों की संख्या(बारंबारता) | ||
|- | |- | ||
|0 – 5 | |0 – 5 | ||
| Line 71: | Line 80: | ||
|20 | |20 | ||
|} | |} | ||
अवर्गीकृत | '''अवर्गीकृत बारंबारता बंटन तालिका''': अवर्गीकृत बारंबारता बंटन तालिका में हम वर्ग अंतराल नहीं बनाते हैं, हम व्यक्तिगत आंकड़ों की सटीक बारंबारता लिखते हैं। उपरोक्त उदाहरण को ध्यान में रखते हुए, अवर्गीकृत सारणी इस प्रकार होगी। नीचे दी गई तालिका में दो स्तम्भ दिखाए गए हैं: एक टेस्ट में प्राप्त अंकों का है और दूसरा बारंबारता (छात्रों की संख्या) का है। | ||
{| class="wikitable" | {| class="wikitable" | ||
! | !परीक्षण में प्राप्त अंक | ||
! | !छात्रों की संख्या | ||
|- | |- | ||
|5 | |5 | ||
| Line 96: | Line 105: | ||
== महत्वपूर्ण टिप्पणियाँ == | == महत्वपूर्ण टिप्पणियाँ == | ||
बारंबारता बंटन से संबंधित महत्वपूर्ण टिप्पणियाँ निम्नलिखित हैं। | |||
* किसी निश्चित उद्देश्य के लिए एकत्रित किए गए आंकड़े या संख्याएँ | * किसी निश्चित उद्देश्य के लिए एकत्रित किए गए आंकड़े या संख्याएँ आंकडाँ कहलाती हैं। | ||
* | * बारंबारता संख्याओं में वह मान है जो दर्शाता है कि दिए गए आंकड़ों के समुच्चय में कोई विशेष वस्तु कितनी बार आती है। | ||
* | * बारंबारता तालिका दो प्रकार की होती है - वर्गीकृत बारंबारता बंटन और अवर्गीकृत बारंबारता बंटन । | ||
* | * आंकड़ों को आयतचित्र(हिस्टोग्राम), दंड आरेख(बार ग्राफ़), बारंबारता बहुभुज(फ़्रीक्वेंसी पॉलीगॉन) आदि जैसे आलेख का उपयोग करके दिखाया जा सकता है। | ||
[[Category:सांख्यिकी]][[Category:कक्षा-11]][[Category:गणित]] | [[Category:सांख्यिकी]][[Category:कक्षा-11]][[Category:गणित]] | ||
Latest revision as of 07:50, 27 November 2024
बारंबारता बंटन, दोहराई गई वस्तुओं की बारंबारता को आलेखी रूप या सारणीबद्ध रूप में दर्शाता है। यह वस्तुओं की बारंबारता का एक दृश्य प्रदर्शन देता है या दिखाता है कि वे कितनी बार घटित हुई हैं। आइए इस लेख में बारंबारता बंटन के बारे में विस्तार से जानें।
परिचय
एकत्रित आंकड़ों को तालिका के रूप में व्यवस्थित करने के लिए बारंबारता बंटन का उपयोग किया जाता है। आंकडें, छात्रों द्वारा प्राप्त अंक, विभिन्न शहरों के तापमान, वॉलीबॉल मैच में प्राप्त अंक आदि हो सकते हैं। आंकड़ों के संग्रह के बाद, हमें बेहतर समझ के लिए आंकड़ों को सार्थक तरीके से दिखाना होगा। आंकड़ों को इस तरह से व्यवस्थित करें कि इसकी सभी विशेषताएँ एक तालिका में संक्षेपित हो जाएँ। इसे बारंबारता बंटन के रूप में जाना जाता है।
इसे बेहतर ढंग से समझने के लिए आइए एक उदाहरण पर विचार करें।
श्री शर्मा जी द्वारा जारी जी.के. प्रश्नोत्तरी में 10 छात्रों के अंक निम्नलिखित हैं । आइए इस आंकड़ों को बारंबारता बंटन में दर्शाते हैं और उन छात्रों की संख्या ज्ञात क हैं जिन्हें समान अंक मिले हैं।
| प्रश्नोत्तरी अंक | छात्रों की संख्या |
|---|---|
| 15 | 2 |
| 17 | 3 |
| 20 | 3 |
| 14 | 2 |
हम देख सकते हैं कि एकत्रित सभी आंकड़ों को प्रश्नोत्तरी अंक और छात्रों की संख्या के स्तंभ के अंतर्गत व्यवस्थित किया गया है। इससे दी गई जानकारी को समझना आसान हो जाता है और हम देख सकते हैं कि समान अंक प्राप्त करने वाले छात्रों की संख्या कितनी है। इस प्रकार, सांख्यिकी में बारंबारता बंटन हमें आंकड़ों को एक दृष्टि में इसकी विशेषताओं को समझने के लिए आसान तरीके से व्यवस्थित करने में मदद करता है।
बारंबारता बंटन आलेख
आंकड़ों को आलेख के रूप में दिखाने का एक और उपाय है और इसे बारंबारता बंटन आलेख का उपयोग करके किया जा सकता है। आलेख हमें एकत्रित आंकड़ों को आसान तरीके से समझने में सहायता करते हैं। बारंबारता बंटन का आलेखी प्रतिनिधित्व निम्नलिखित का उपयोग करके दिखाया जा सकता है:
- दंड आरेख(बार ग्राफ): दंड आरेख आयताकार दंडों के बीच समान दूरी के साथ समान चौड़ाई के आयताकार दंडों का उपयोग करके आंकड़ों का प्रतिनिधित्व करते हैं।
- आयतचित्र(हिस्टोग्राम): आयतचित्र विभिन्न ऊंचाइयों के आयताकार दंडों का उपयोग करके आंकड़ों की एक आलेखी प्रस्तुति है। आयतचित्र में, आयताकार दंडों के बीच कोई जगह नहीं होती है।
- पाइ रेखाचित्र(पाई चार्ट): पाइ रेखाचित्र एक प्रकार का आलेख है जो आंकड़ों को एक गोलाकार(वृत) चार्ट में प्रदर्शित करता है। यह आंकड़ों को एक गोलाकार तरीके से अभिलेख करता है और फिर इसे आगे वृतखंडों(सेक्टरों) में विभाजित किया जाता है जो पूरे भागों में से आंकड़ों का एक विशेष भाग दिखाते हैं।
- बारंबारता बहुभुज: आयतचित्र में दंडों के मध्य-बिंदुओं को जोड़कर एक बारंबारता बहुभुज बनाया जाता है।
बारंबारता बंटन के प्रकार
सांख्यिकी के अंतर्गत बारंबारता बंटन के चार प्रकार हैं, जिन्हें नीचे समझाया गया है:
अवर्गीकृत बारंबारता बंटन : यह आंकड़ों मानों के समूहों के बजाय प्रत्येक अलग-अलग आंकड़ों मान में किसी वस्तु(आइटम) की बारंबारता दिखाता है।
वर्गीकृत बारंबारता बंटन : इस प्रकार में, आंकड़ों को व्यवस्थित किया जाता है और उन्हें वर्ग अंतराल नामक समूहों में विभाजित किया जाता है। प्रत्येक वर्ग अंतराल से संबंधित आंकड़ों की बारंबारता को बारंबारता बंटन तालिका में अभिलेख किया जाता है। वर्गीकृत बारंबारता तालिका वर्ग अंतराल में आवृत्तियों के बंटन को दर्शाती है।
सापेक्ष बारंबारता बंटन : यह प्रत्येक श्रेणी से जुड़े कुल प्रेक्षणों की संख्या के अनुपात को बताता है।
संचयी बारंबारता बंटन : यह बारंबारता बंटन में पहली बारंबारता और उसके नीचे की सभी बारंबारता का योग है। आपको अगले मान के साथ एक मान जोड़ना होगा फिर अगले मान के साथ योग को फिर से जोड़ना होगा और इसी तरह अंतिम तक करना होगा। अंतिम संचयी बारंबारता सभी बारंबारता का कुल योग होगी।
बारंबारता बंटन तालिका
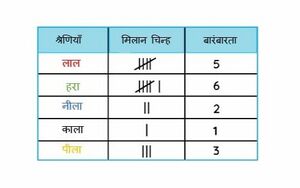
बारंबारता बंटन तालिका एक चार्ट है जो आंकड़ों के समुच्चय में प्रत्येक वस्तु की बारंबारता को दर्शाता है। आइए मिलान चिन्ह का उपयोग करके बारंबारता बंटन तालिका बनाने के तरीके को समझने के लिए एक उदाहरण पर विचार करें।
एक कलश जिसमें विभिन्न रंगों के मोती हैं- लाल, हरा, नीला, काला, लाल, हरा, नीला, पीला, लाल, लाल, हरा, हरा, हरा, पीला, लाल, हरा, पीला। प्रत्येक विशेष रंग के मोतियों की सही संख्या जानने के लिए, हमें मोतियों को श्रेणियों में वर्गीकृत करना होगा। प्रत्येक रंग के मोतियों की संख्या का पता लगाने का एक आसान उपाय मिलान चिन्ह का उपयोग करना है। मोतियों को एक-एक करके चुनें और संबंधित पंक्ति और स्तम्भ में मिलान चिन्ह दर्ज करें। फिर, तालिका में प्रत्येक वस्तु के लिए बारंबारता इंगित करें।
इस प्रकार, प्राप्त तालिका को बारंबारता बंटनतालिका कहा जाता है।
बारंबारता बंटन तालिका के प्रकार
बारंबारता बंटन तालिकाएँ दो प्रकार की होती हैं: वर्गीकृत और अवर्गीकृत बारंबारता बंटनता लिकाएँ।
वर्गीकृत बारंबारता बंटन तालिका: बड़ी संख्या में प्रेक्षणों या आंकड़ों को व्यवस्थित करने के लिए, हम वर्गीकृत बारंबारता बंटन तालिका का उपयोग करते हैं। इसमें, हम उस विशेष वर्ग अंतराल से संबंधित आंकड़ों की बारंबारता का मिलान करने के लिए वर्ग अंतराल बनाते हैं।
उदाहरण के लिए, टेस्ट में 20 छात्रों द्वारा प्राप्त अंक इस प्रकार हैं। । वर्गीकृत तालिका में आंकड़ों को व्यवस्थित करने के लिए हमें वर्ग अंतराल बनाने होंगे। इस प्रकार, हम और इसी तरह के अंकों के वर्ग अंतराल बनाएंगे। नीचे दी गई तालिका में दो स्तम्भ दिखाए गए हैं, एक वर्ग अंतराल (परीक्षण में प्राप्त अंक) का है और दूसरा बारंबारता (छात्रों की संख्या) का है। इसमें हमने मिलान चिन्ह का उपयोग नहीं किया है क्योंकि हमने अंकों की सीधे गणना की है।
| परीक्षण में प्राप्त अंक(वर्ग अंतराल) | छात्रों की संख्या(बारंबारता) |
|---|---|
| 0 – 5 | 3 |
| 6 – 10 | 4 |
| 11 – 15 | 5 |
| 16 – 20 | 8 |
| Total | 20 |
अवर्गीकृत बारंबारता बंटन तालिका: अवर्गीकृत बारंबारता बंटन तालिका में हम वर्ग अंतराल नहीं बनाते हैं, हम व्यक्तिगत आंकड़ों की सटीक बारंबारता लिखते हैं। उपरोक्त उदाहरण को ध्यान में रखते हुए, अवर्गीकृत सारणी इस प्रकार होगी। नीचे दी गई तालिका में दो स्तम्भ दिखाए गए हैं: एक टेस्ट में प्राप्त अंकों का है और दूसरा बारंबारता (छात्रों की संख्या) का है।
| परीक्षण में प्राप्त अंक | छात्रों की संख्या |
|---|---|
| 5 | 3 |
| 10 | 4 |
| 15 | 5 |
| 18 | 4 |
| 20 | 4 |
| Total | 20 |
महत्वपूर्ण टिप्पणियाँ
बारंबारता बंटन से संबंधित महत्वपूर्ण टिप्पणियाँ निम्नलिखित हैं।
- किसी निश्चित उद्देश्य के लिए एकत्रित किए गए आंकड़े या संख्याएँ आंकडाँ कहलाती हैं।
- बारंबारता संख्याओं में वह मान है जो दर्शाता है कि दिए गए आंकड़ों के समुच्चय में कोई विशेष वस्तु कितनी बार आती है।
- बारंबारता तालिका दो प्रकार की होती है - वर्गीकृत बारंबारता बंटन और अवर्गीकृत बारंबारता बंटन ।
- आंकड़ों को आयतचित्र(हिस्टोग्राम), दंड आरेख(बार ग्राफ़), बारंबारता बहुभुज(फ़्रीक्वेंसी पॉलीगॉन) आदि जैसे आलेख का उपयोग करके दिखाया जा सकता है।