रोले का प्रमेय

कैलकुलस में, रोले का प्रमेय बताता है कि यदि कोई अवकलनीय फ़ंक्शन (वास्तविक-मूल्यवान) दो अलग-अलग बिंदुओं पर समान मान प्राप्त करता है, तो उसके बीच कहीं न कहीं कम से कम एक निश्चित बिंदु अवश्य होना चाहिए, जहाँ पहला व्युत्पन्न शून्य हो। रोले के प्रमेय का नाम फ्रांसीसी गणितज्ञ मिशेल रोले के नाम पर रखा गया है। रोले का प्रमेय माध्य मान प्रमेय का एक विशेष मामला है।

लैग्रेंज के माध्य मान प्रमेय को माध्य मान प्रमेय या प्रथम माध्य मान प्रमेय भी कहा जाता है। आमतौर पर, माध्य को दिए गए मानों का औसत माना जाता है, लेकिन समाकल के मामले में, दो अलग-अलग फ़ंक्शनों का माध्य मान ज्ञात करने की विधि अलग होती है। इस लेख में आइए रोले के प्रमेय और ऐसे फ़ंक्शनों के माध्य मान के साथ-साथ उनकी ज्यामितीय व्याख्या के बारे में जानें।

परिभाषा

रोले के प्रमेय का अध्ययन करने से पहले आइए कैलकुलस में लैग्रेंज के माध्य मान प्रमेय को समझें।

लैग्रेंज का माध्य मान प्रमेय कथन:

माध्य मान प्रमेय बताता है कि "यदि एक फ़ंक्शन f को बंद अंतराल $[a,b]$ पर परिभाषित किया जाता है जो निम्नलिखित शर्तों को संतुष्ट करता है: i) फ़ंक्शन f बंद अंतराल $[a,b]$ पर निरंतर है और ii) फ़ंक्शन $f$ खुले अंतराल $(a,b)$ पर अवकलनीय है। तब एक मान $x=c$ इस तरह से मौजूद होता है कि $f'(c)=[f(b)-f(a)]/(b-a)''$।

इस प्रमेय को "प्रथम माध्य मान प्रमेय" के नाम से भी जाना जाता है। लैग्रेंज के माध्य मान प्रमेय का एक विशेष मामला रोले का प्रमेय है। आइए अब समझते हैं कि रोले का प्रमेय क्या है।

रोले का प्रमेय कथन

रोले का प्रमेय कहता है कि "यदि एक फ़ंक्शन $f$ को बंद अंतराल $[a,b]$ में इस तरह से परिभाषित किया जाता है कि यह निम्नलिखित शर्त को संतुष्ट करता है: i) $f[a,b]$ पर निरंतर है, ii)$f(a,b)$ पर अवकलनीय है, और iii) $f(a)=f(b),$ तो $x$ का कम से कम एक मान मौजूद है, आइए हम इस मान को $c$ मानें, जो $a$ और $b$ के बीच स्थित है यानी $(a<c<b)$ इस तरह से कि $f'(c)=0$."

गणितीय रूप से, रोले के प्रमेय को इस प्रकार कहा जा सकता है: मान लें कि $f:[a,b]\rightarrow R,[a,b]$ पर सतत है और $(a,b)$ पर अवकलनीय है, जैसे कि $f(a)=f(b),$ जहाँ $a$ और $b$ कुछ वास्तविक संख्याएँ हैं। तब $(a,b)$ में कुछ $c$ मौजूद होता है जैसे कि $f'(c)=0$

रोले के प्रमेय की ज्यामितीय व्याख्या

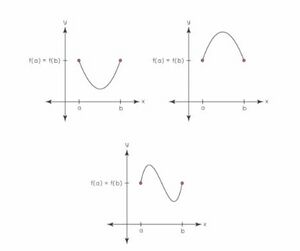
रोले के प्रमेय की ज्यामितीय व्याख्या

दिए गए ग्राफ में, वक्र $y=f(x),$ $x=a$और $x=b$ के बीच सतत है और अंतराल के भीतर प्रत्येक बिंदु पर, भुज के अनुरूप एक स्पर्शरेखा और निर्देशांक खींचना संभव है और बराबर हैं, तो वक्र के लिए कम से कम एक स्पर्शरेखा मौजूद है जो x-अक्ष के समानांतर है। बीजगणितीय रूप से, यह प्रमेय हमें बताता है कि यदि $f(x),\ x$ में एक बहुपद फलन को दर्शाता है और समीकरण$f(x)=0$ के दो मूल $x=a$ और $x=b$ हैं, तो समीकरण $f'(x)=0$ का कम से कम एक मूल इन मानों के बीच स्थित होता है। रोले के प्रमेय का विलोम सत्य नहीं है और यह भी संभव है कि $x$ के एक से अधिक मान मौजूद हों, जिसके लिए प्रमेय सही है लेकिन ऐसे एक मान के अस्तित्व की निश्चित संभावना है।

रोले के प्रमेय का प्रमाण

जब किसी प्रमेय को सीधे सिद्ध किया जाता है, तो आप यह मानकर शुरू करते हैं कि सभी शर्तें पूरी हो चुकी हैं। इसलिए, नीचे दी गई हमारी चर्चा केवल उन कार्यों से संबंधित है

जो $[a,b]$ पर निरंतर है,

जो अवकलनीय $(a,b)$ है,

और जिसमें $f(a)=f(b)$ है।

इसे ध्यान में रखते हुए, ध्यान दें कि जब कोई फ़ंक्शन रोले के प्रमेय को संतुष्ट करता है, तो वह स्थान जहाँ $f'(x)=0$अधिकतम या न्यूनतम मान (यानी, चरम) पर होता है।

हमें कैसे पता चलेगा कि किसी फ़ंक्शन में इनमें से कोई एक चरम भी होगा? चरम मान प्रमेय प्रमेय कहता है कि यदि कोई फ़ंक्शन निरंतर है, तो अंतराल में अधिकतम और न्यूनतम दोनों बिंदु होने की गारंटी है।

अब, हमारे फ़ंक्शन के लिए दो बुनियादी संभावनाएँ हैं।

स्थिति 1: फलन स्थिर है।

फलन स्थिर नहीं

स्थिति 2: फलन स्थिर नहीं है।

आइए हम इनमें से प्रत्येक मामले पर अधिक विस्तार से नज़र डालें।

स्थिति 1: फ़ंक्शन स्थिर है

स्थिर फ़ंक्शन के लिए, ग्राफ़ एक क्षैतिज रेखा खंड होता है।

इस मामले में, हर बिंदु रोले के प्रमेय को संतुष्ट करता है क्योंकि व्युत्पन्न हर जगह शून्य है। (याद रखें, रोले का प्रमेय कम से कम एक बिंदु की गारंटी देता है। यह कई बिंदुओं को रोकता नहीं है!)

स्थिति 2: फ़ंक्शन स्थिर नहीं है।

चूँकि फ़ंक्शन स्थिर नहीं है, इसलिए इसे उसी y-मान पर शुरू और समाप्त करने के लिए दिशाएँ बदलनी चाहिए। इसका मतलब है कि अंतराल के भीतर किसी बिंदु पर फ़ंक्शन में या तो न्यूनतम, अधिकतम या दोनों होंगे। इसलिए, अब हमें यह दिखाने की ज़रूरत है कि इस आंतरिक-बिंदु पर व्युत्पन्न शून्य के बराबर है। बाकी चर्चा उन मामलों पर केंद्रित होगी जहाँ आंतरिक चरम सीमा अधिकतम है, लेकिन न्यूनतम के लिए चर्चा काफी हद तक समान है।

संभावना 1: क्या अधिकतम उस बिंदु पर हो सकता है जहाँ $f'>0$ है?

नहीं, क्योंकि अगर $f'>0$ है तो हम जानते हैं कि फ़ंक्शन बढ़ रहा है। लेकिन यह बढ़ नहीं सकता क्योंकि हम इसके अधिकतम बिंदु पर हैं।

संभावना 2: क्या अधिकतम उस बिंदु पर हो सकता है जहाँ $f'<0$ है?

नहीं, क्योंकि अगर $f'<0$ है तो हम जानते हैं कि फ़ंक्शन घट रहा है, जिसका अर्थ है कि यह हमारे वर्तमान स्थान से थोड़ा बाईं ओर बड़ा था। लेकिन हम फ़ंक्शन के अधिकतम मान पर हैं, इसलिए यह बड़ा नहीं हो सकता था। चूँकि f′ मौजूद है, लेकिन शून्य से बड़ा नहीं है, और शून्य से छोटा नहीं है, इसलिए एकमात्र संभावना यह है कि $f'=0$ है। और बस! हमने दिखाया है कि फ़ंक्शन में चरम सीमा होनी चाहिए और चरम सीमा पर व्युत्पन्न शून्य के बराबर होना चाहिए!

उदाहरण

उदाहरण : फ़ंक्शन $y=x^{2}+1,$ $a=-1$ और $b=1$ के लिए रोले प्रमेय का सत्यापन करें।

हल: फ़ंक्शन $y=x^{2}+1,$ क्योंकि यह एक बहुपद फ़ंक्शन है, $[-1,1]$ में सतत है और $(-1,1)$ में अवकलनीय है।

साथ ही, $f(-1)=(-1)^{2}+1=1+1=2f(1)=(1)^{2}+1=1+1=2$

इस प्रकार, $f(-1)=f(1)=2$

अतः, फ़ंक्शन $f(x)$ रोले प्रमेय की सभी शर्तों को संतुष्ट करता है।

अब,$f'(x)=2x$ रोले प्रमेय बताता है कि एक बिंदु $c\in (-2,2)$ ऐसा है कि

$f'(c)=0$

$2c=0$

$c=0$ जहाँ $c=0\in (-1,1)$

उत्तर: अतः रोले का प्रमेय सत्यापित है।