उच्चतम और निम्नतम: Difference between revisions

Latest revision as of 21:22, 3 December 2024

उच्चतम और निम्नतम को फलन के चरम के रूप में जाना जाता है। उच्चतम और निम्नतम किसी फलन के दिए गए परिसर के समुच्चय के भीतर अधिकतम या न्यूनतम मान हैं। फलन के लिए, सम्पूर्ण परिसर के अंतर्गत, फलन के अधिकतम मान को निरपेक्ष उच्चतम के रूप में जाना जाता है और न्यूनतम मान को निरपेक्ष निम्नतम के रूप में जाना जाता है।

फलन के अन्य उच्चतम और निम्नतम होते हैं, जो फलन के निरपेक्ष उच्चतम और निम्नतम नहीं होते हैं और उन्हें स्थानीय उच्चतम और स्थानीय निम्नतम के रूप में जाना जाता है। आइए स्थानीय उच्चतम और निम्नतम , निरपेक्ष उच्चतम और निम्नतम के बारे में और जानें और फलन के उच्चतम और निम्नतम को ज्ञात करने की विधि को भी जानने का प्रयास करें ।

परिभाषा

उच्चतम और निम्नतम

उच्चतम और निम्नतम किसी फलन के वक्र में चोटियाँ और घाटियाँ हैं। किसी फलन के लिए उच्चतम और निम्नतम की कोई भी संख्या हो सकती है। कलन में, हम फलन के आलेख को देखे बिना भी किसी फलन का अधिकतम और न्यूनतम मान पा सकते हैं। उच्चतम दी गई सीमा के भीतर वक्र पर सबसे ऊँचा बिंदु होगा और निम्नतम वक्र पर सबसे निचला बिंदु होगा।

उच्चतम और निम्नतम का संयोजन चरम है। नीचे दी गई छवि में, हम आलेख में विभिन्न चोटियाँ और घाटियाँ देख सकते हैं। $x=a$ और $x=0$ पर, हमें फलन के अधिकतम मान मिलते हैं, और $x=b$ और $x=c$ पर, हमें फलन के न्यूनतम मान मिलते हैं। सभी चोटियाँ उच्चतम हैं और घाटियाँ निम्नतम हैं।

किसी फलन में दो प्रकार के उच्चतम और निम्नतम उपस्थित होते हैं, जो हैं:

स्थानीय उच्चतम और निम्नतम
निरपेक्ष या सार्वत्रिक उच्चतम और निम्नतम

आइए इनके बारे में विस्तार से जानें।

स्थानीय अधिकतम और न्यूनतम

स्थानीय उच्चतम और निम्नतम

स्थानीय अधिकतम और न्यूनतम फलन के अधिकतम और न्यूनतम हैं, जो किसी विशेष अंतराल में उत्पन्न होते हैं। स्थानीय अधिकतम एक विशेष अंतराल में एक बिंदु पर फलन का मान होगा जिसके लिए उस बिंदु के पास फलन के मान सड़ाईव उस बिंदु पर फलन के मान से कम होते हैं। जबकि स्थानीय न्यूनतम उस बिंदु पर फलन का मान होगा जहाँ उस बिंदु के पास फलन के मान उस बिंदु पर फलन के मान से अधिक होते हैं।

स्थानीय अधिकतम: एक बिंदु $x=b$ , $f(x)$ के लिए स्थानीय अधिकतम का एक बिंदु है यदि $b$ के प्रतिवेश में है यानी $(b-\delta ,b+\delta )$ में जहाँ $\delta$ को मनमाने ढंग से छोटा किया जा सकता है, $f(x)<f(b)$ सभी $x\in {(b-\delta ,b+\delta )}/\{b\}$ के लिए। इसका सीधा सा अर्थ है कि अगर हम $x=b$ के आस-पास एक छोटा क्षेत्र (अंतराल) मानते हैं, तो $f(b)$ उस अंतराल में अधिकतम होना चाहिए।

स्थानीय न्यूनतम: एक बिंदु $x=a$ , $f(x)$ के लिए स्थानीय न्यूनतम का एक बिंदु है यदि $a$ के प्रतिवेश में है, यानी $(a-\delta ,a+\delta )$ में, (जहाँ $\delta$ के मनमाने ढंग से छोटे मान हो सकते हैं), $f(x)>f(a)$ सभी $x\in {(a-\delta ,a+\delta )}/\{a\}$ के लिए। इसका अर्थ यह है कि यदि हम $x=a$ के आस-पास एक छोटा अंतराल लें, तो $f(a)$ उस अंतराल में न्यूनतम होना चाहिए।

नीचे दी गई छवि में, हम देख सकते हैं कि $x=b$ और $x=d$ , स्थानीय उच्चतम हैं, और $x=a$ और $x=c$ , स्थानीय निम्नतम हैं।

निरपेक्ष उच्चतम और निम्नतम

सम्पूर्णउच्चतम और निम्नतम

सम्पूर्ण प्रांत के भीतर किसी फलन का उच्चतम बिंदु फलन का निरपेक्ष उच्चतम कहलाता है, जबकि फलन के सम्पूर्ण प्रांत के भीतर फलन का निम्नतम बिंदु फलन का निरपेक्ष निम्नतम कहलाता है। सम्पूर्ण प्रांत पर फलन का केवल एक निरपेक्ष उच्चतम और फलन का एक निरपेक्ष निम्नतम हो सकता है। फलन के निरपेक्ष उच्चतम और निम्नतम को फलन का सार्वत्रिक उच्चतम और सार्वत्रिक निम्नतम भी कहा जा सकता है।

निरपेक्ष उच्चतम : एक बिंदु $x=af(x)$ के लिए सार्वत्रिक उच्चतम का बिंदु है यदि सभी $x\in D,(f(x)$ का प्रांत $)$ के लिए $f(x)\leq f(a)$ है।

निरपेक्ष निम्नतम: एक बिंदु $x=af(x)$ के लिए सार्वत्रिक निम्नतम का बिंदु है यदि सभी $x\in D,(f(x)$ का प्रांत $)$ के लिए $f(x)\geq f(a)$ है।

नीचे दी गई छवि में, बिंदु $x=a$ फलन का निरपेक्ष उच्चतम है और $x=b$ पर फलन का निरपेक्ष निम्नतम है।

किसी फलन का उच्चतम और निम्नतम ज्ञात करने की विधि

फलन का उच्चतम और निम्नतम पहले-कोटी अवकलन परीक्षण और दूसरे-कोटी अवकलन परीक्षण का उपयोग करके गणना की जा सकती है। अवकलन परीक्षण किसी फलन का उच्चतम और निम्नतम खोजने का सबसे तेज़ तरीका है। आइए हम उन पर एक-एक करके चर्चा करें।

उच्चतम और निम्नतम के लिए, प्रथम कोटी अवकलन परीक्षण

किसी फलन का पहला अवकलन फलन का ढलान देता है। अधिकतम बिंदु के पास, वक्र का ढलान बढ़ता है क्योंकि हम अधिकतम बिंदु की ओर बढ़ते हैं फिर अधिकतम बिंदु पर $0$ हो जाता है और फिर अधिकतम बिंदु से दूर जाने पर घटता है। इसी तरह, न्यूनतम बिंदु के पास, फलन का ढलान घटता है क्योंकि हम न्यूनतम बिंदु की ओर बढ़ते हैं फिर न्यूनतम बिंदु पर $0$ हो जाता है और फिर न्यूनतम बिंदु से दूर जाने पर बढ़ता है। हम इस जानकारी का उपयोग यह जानने के लिए करते हैं कि बिंदु अधिकतम है या न्यूनतम।

मान लें कि हमारे पास एक फलन $f$ है जो एक खुले अंतराल $I$ में परिभाषित छिद्रान्वेषी बिंदु पर निरंतर है और $f'(c)=0$ (ढलान $c$ पर $0$ है)। फिर हम वक्र के बाईं ओर और वक्र के दाईं ओर बिंदु पर $f'(x)$ का मान जाँचते हैं और $f'(x)$ की प्रकृति की जाँच करते हैं, फिर हम कह सकते हैं कि दिया गया बिंदु होगा:

स्थानीय उच्चतम : यदि बिंदु $c$ से $x$ बढ़ने पर $f'(x)$ का चिह्न धनात्मक से ऋणात्मक में बदल जाता है, तो $f(c)$ उस श्रेणी में फलन का अधिकतम मान देता है।
स्थानीय निम्नतम : यदि बिंदु $c$ से $x$ बढ़ने पर $f'(x)$ का चिह्न ऋणात्मक से धनात्मक में बदल जाता है, तो $f(c)$ उस श्रेणी में फलन का न्यूनतम मान देता है।
परिवर्तन बिंदु: यदि $c$ से $x$ बढ़ने पर $f'(x)$ का चिह्न नहीं बदलता है, और बिंदु $c$ फलन का न तो उच्चतम है और न ही निम्नतम , तो बिंदु $c$ को विभक्ति बिंदु कहा जाता है।

उच्चतम और निम्नतम के लिए, द्वितीय कोटी अवकलन परीक्षण

उच्चतम और निम्नतम के लिए द्वितीय-कोटी अवकलन परीक्षण में, हम फलन का पहला अवकलन पाते हैं और यदि यह छिद्रान्वेषी बिंदु $x=c(f'(c)=0)$ पर ढलान का मान $0$ के बराबर देता है, तो हम फलन का दूसरा अवकलन पाते हैं। यदि फलन का दूसरा अवकलन दी गई सीमा के भीतर उपस्थित है, तो दिया गया बिंदु निमलिखित प्रकार होगा:

स्थानीय अधिकतम: यदि $f''(c)<0$
स्थानीय न्यूनतम: यदि $f''(c)>0$
परीक्षण विफल: यदि $f''(c)=0$

महत्वपूर्ण टिप्पणियाँ

उच्चतम और निम्नतम किसी फलन के वक्र में चोटियाँ और घाटियाँ हैं।
किसी फलन का केवल एक निरपेक्ष उच्चतम और पूरे प्रांत पर फलन का एक निरपेक्ष निम्नतम हो सकता है।
अंतराल $I$ में फलन $f$ को एक एकदिष्ट (मोनोटोनॉस)फलन कहा जाता है, यदि $f$ या तो $I$ में बढ़ रहा है या $I$ में घट रहा है।

@@ Line 1: / Line 1: @@
-मैक्सिमा और मिनिमा को फ़ंक्शन के चरम के रूप में जाना जाता है। मैक्सिमा और मिनिमा किसी फ़ंक्शन के दिए गए रेंज के सेट के भीतर अधिकतम या न्यूनतम मान हैं। फ़ंक्शन के लिए, संपूर्ण रेंज के अंतर्गत, फ़ंक्शन के अधिकतम मान को निरपेक्ष मैक्सिमा के रूप में जाना जाता है और न्यूनतम मान को निरपेक्ष मिनिमा के रूप में जाना जाता है।
+उच्चतम और निम्नतम  को फलन के चरम के रूप में जाना जाता है। उच्चतम और निम्नतम  किसी फलन के दिए गए परिसर के [[समुच्चय और उनका निरूपण|समुच्चय]] के भीतर अधिकतम या न्यूनतम मान हैं। फलन के लिए, सम्पूर्ण परिसर के अंतर्गत, फलन के अधिकतम मान को निरपेक्ष उच्चतम के रूप में जाना जाता है और न्यूनतम मान को निरपेक्ष निम्नतम के रूप में जाना जाता है।
-फ़ंक्शन के अन्य मैक्सिमा और मिनिमा होते हैं, जो फ़ंक्शन के निरपेक्ष मैक्सिमा और मिनिमा नहीं होते हैं और उन्हें स्थानीय मैक्सिमा और स्थानीय मिनिमा के रूप में जाना जाता है। आइए स्थानीय मैक्सिमा और मिनिमा, निरपेक्ष मैक्सिमा और मिनिमा के बारे में और जानें और फ़ंक्शन के मैक्सिमा और मिनिमा को कैसे खोजें।
+फलन के अन्य उच्चतम और निम्नतम  होते हैं, जो फलन के निरपेक्ष उच्चतम और निम्नतम  नहीं होते हैं और उन्हें स्थानीय उच्चतम और स्थानीय निम्नतम के रूप में जाना जाता है। आइए स्थानीय उच्चतम और निम्नतम , निरपेक्ष उच्चतम और निम्नतम  के बारे में और जानें और फलन के उच्चतम और निम्नतम को ज्ञात करने की विधि को भी जानने का प्रयास करें ।
-== किसी फ़ंक्शन के मैक्सिमा और मिनिमा क्या हैं? ==
+== परिभाषा ==
-मैक्सिमा और मिनिमा किसी फ़ंक्शन के वक्र में चोटियाँ और घाटियाँ हैं। किसी फ़ंक्शन के लिए मैक्सिमा और मिनिमा की कोई भी संख्या हो सकती है। कैलकुलस में, हम फ़ंक्शन के ग्राफ़ को देखे बिना भी किसी फ़ंक्शन का अधिकतम और न्यूनतम मान पा सकते हैं। मैक्सिमा दी गई सीमा के भीतर वक्र पर सबसे ऊँचा बिंदु होगा और मिनिमा वक्र पर सबसे निचला बिंदु होगा।
+[[File:उच्चतम और निम्नतम.jpg|thumb|उच्चतम और निम्नतम]]
+उच्चतम और निम्नतम  किसी [[फलनों के प्राचलिक रूपों के अवकलज|फलन]] के वक्र में चोटियाँ और घाटियाँ हैं। किसी फलन के लिए उच्चतम और निम्नतम  की कोई भी संख्या हो सकती है। कलन में, हम फलन के आलेख को देखे बिना भी किसी फलन का अधिकतम और न्यूनतम मान पा सकते हैं। उच्चतम दी गई सीमा के भीतर वक्र पर सबसे ऊँचा बिंदु होगा और निम्नतम वक्र पर सबसे निचला बिंदु होगा।
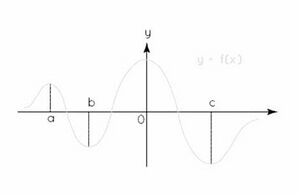
-मैक्सिमा और मिनिमा का संयोजन चरम है। नीचे दी गई छवि में, हम ग्राफ़ में विभिन्न चोटियाँ और घाटियाँ देख सकते हैं। x = a और x = 0 पर, हमें फ़ंक्शन के अधिकतम मान मिलते हैं, और x = b और x = c पर, हमें फ़ंक्शन के न्यूनतम मान मिलते हैं। सभी चोटियाँ मैक्सिमा हैं और घाटियाँ मिनिमा हैं।
+उच्चतम और निम्नतम  का संयोजन चरम है। नीचे दी गई छवि में, हम आलेख में विभिन्न चोटियाँ और घाटियाँ देख सकते हैं। <math>x = a</math> और <math>x = 0</math> पर, हमें फलन के अधिकतम मान मिलते हैं, और <math>x = b</math> और <math>x = c </math> पर, हमें फलन के न्यूनतम मान मिलते हैं। सभी चोटियाँ उच्चतम हैं और घाटियाँ निम्नतम हैं।
+किसी फलन में दो प्रकार के उच्चतम और निम्नतम उपस्थित होते हैं, जो हैं:
+* स्थानीय उच्चतम और निम्नतम
-किसी फ़ंक्शन में दो प्रकार के मैक्सिमा और मिनिमा मौजूद होते हैं, जो हैं:
+* निरपेक्ष या सार्वत्रिक उच्चतम और निम्नतम
-स्थानीय मैक्सिमा और मिनिमा
-पूर्ण या वैश्विक मैक्सिमा और मिनिमा
 आइए इनके बारे में विस्तार से जानें।
 == स्थानीय अधिकतम और न्यूनतम ==
-स्थानीय अधिकतम और न्यूनतम फ़ंक्शन के अधिकतम और न्यूनतम हैं जो किसी विशेष अंतराल में उत्पन्न होते हैं। स्थानीय अधिकतम एक विशेष अंतराल में एक बिंदु पर फ़ंक्शन का मान होगा जिसके लिए उस बिंदु के पास फ़ंक्शन के मान हमेशा उस बिंदु पर फ़ंक्शन के मान से कम होते हैं। जबकि स्थानीय न्यूनतम उस बिंदु पर फ़ंक्शन का मान होगा जहाँ उस बिंदु के पास फ़ंक्शन के मान उस बिंदु पर फ़ंक्शन के मान से अधिक होते हैं।
+[[File:स्थानीय उच्चतम और निम्नतम.jpg|thumb|स्थानीय उच्चतम और निम्नतम]]
+स्थानीय अधिकतम और न्यूनतम फलन के अधिकतम और न्यूनतम हैं, जो किसी विशेष अंतराल में उत्पन्न होते हैं। स्थानीय अधिकतम एक विशेष अंतराल में एक बिंदु पर फलन का मान होगा जिसके लिए उस बिंदु के पास फलन के मान सड़ाईव उस बिंदु पर फलन के मान से कम होते हैं। जबकि स्थानीय न्यूनतम उस बिंदु पर फलन का मान होगा जहाँ उस बिंदु के पास फलन के मान उस बिंदु पर फलन के मान से अधिक होते हैं।
-स्थानीय अधिकतम: एक बिंदु x = b, f(x) के लिए स्थानीय अधिकतम का एक बिंदु है यदि b के पड़ोस में है यानी (b−𝛿, b+𝛿) में जहाँ 𝛿 को मनमाने ढंग से छोटा किया जा सकता है, f(x) < f(b) सभी x ∈ (b−𝛿, b+𝛿)∖{b} के लिए। इसका सीधा सा मतलब है कि अगर हम x = b के आस-पास एक छोटा क्षेत्र (अंतराल) मानते हैं, तो f(b) उस अंतराल में अधिकतम होना चाहिए।
-स्थानीय न्यूनतम: एक बिंदु x = a, f(x) के लिए स्थानीय न्यूनतम का एक बिंदु है यदि a के पड़ोस में है, यानी (a−𝛿,a+𝛿) में, (जहाँ 𝛿 के मनमाने ढंग से छोटे मान हो सकते हैं), f(x) > f(a) सभी x ∈ (a−𝛿,a+𝛿)∖{a} के लिए। इसका अर्थ यह है कि यदि हम x = a के आस-पास एक छोटा अंतराल लें, तो f(a) उस अंतराल में न्यूनतम होना चाहिए।
-नीचे दी गई छवि में, हम देख सकते हैं कि x = b और x = d, स्थानीय उच्चिष्ठ हैं, और x = a और x = c, स्थानीय निम्निष्ठ हैं।
-== निरपेक्ष मैक्सिमा और मिनिमा ==
+'''स्थानीय अधिकतम''': एक बिंदु <math>x = b</math>, <math>f(x)</math> के लिए स्थानीय अधिकतम का एक बिंदु है यदि <math>b</math> के प्रतिवेश  में है यानी <math>(b-\delta, b+\delta)</math> में जहाँ <math>\delta</math> को मनमाने ढंग से छोटा किया जा सकता है, <math>f(x) < f(b)</math> सभी <math>x\in    {(b -\delta, b +\delta)} /\{ b\}</math> के लिए। इसका सीधा सा अर्थ है कि अगर हम <math>x = b</math> के आस-पास एक छोटा क्षेत्र (अंतराल) मानते हैं, तो <math>f(b)</math> उस अंतराल में अधिकतम होना चाहिए।
-संपूर्ण डोमेन के भीतर किसी फ़ंक्शन का उच्चतम बिंदु फ़ंक्शन का निरपेक्ष मैक्सिमा कहलाता है जबकि फ़ंक्शन के संपूर्ण डोमेन के भीतर फ़ंक्शन का निम्नतम बिंदु फ़ंक्शन का निरपेक्ष मिनिमा कहलाता है। संपूर्ण डोमेन पर फ़ंक्शन का केवल एक निरपेक्ष मैक्सिमा और फ़ंक्शन का एक निरपेक्ष मिनिमा हो सकता है। फ़ंक्शन के निरपेक्ष मैक्सिमा और मिनिमा को फ़ंक्शन का वैश्विक मैक्सिमा और वैश्विक मिनिमा भी कहा जा सकता है।
-निरपेक्ष मैक्सिमा: एक बिंदु x = a f(x) के लिए वैश्विक मैक्सिमा का बिंदु है यदि सभी x∈D (f(x) का डोमेन) के लिए f(x) ≤ f(a) है।
+'''स्थानीय न्यूनतम''': एक बिंदु <math>x = a</math>, <math>f(x)</math> के लिए स्थानीय न्यूनतम का एक बिंदु है यदि <math>a </math> के प्रतिवेश  में है, यानी <math>(a -\delta, a +\delta)</math> में, (जहाँ <math>\delta</math> के मनमाने ढंग से छोटे मान हो सकते हैं),<math>f(x)> f(a)</math> सभी  <math>x\in    {(a -\delta, a +\delta)} / \{a\}</math> के लिए। इसका अर्थ यह है कि यदि हम <math>x = a</math> के आस-पास एक छोटा अंतराल लें, तो <math>f(a)</math> उस अंतराल में न्यूनतम होना चाहिए।
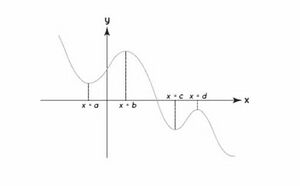
-निरपेक्ष मिनिमा: एक बिंदु x = a f(x) के लिए वैश्विक मिनिमा का बिंदु है यदि सभी x∈D (f(x) का डोमेन) के लिए f(x) ≥ f(a) है।
+नीचे दी गई छवि में, हम देख सकते हैं कि <math>x = b</math> और  <math>x = d</math>, स्थानीय उच्चतम   हैं, और <math>x = a</math> और <math>x = c</math>, स्थानीय निम्नतम  हैं।
+== निरपेक्ष उच्चतम और निम्नतम ==
+[[File:निरपेक्ष उच्चतम और निम्नतम.jpg|thumb|सम्पूर्णउच्चतम और निम्नतम]]
+सम्पूर्ण प्रांत के भीतर किसी फलन का उच्चतम बिंदु फलन का निरपेक्ष उच्चतम कहलाता है, जबकि फलन के  सम्पूर्ण प्रांत के भीतर फलन का निम्नतम बिंदु फलन का निरपेक्ष निम्नतम कहलाता है। सम्पूर्ण प्रांत पर फलन का केवल एक निरपेक्ष उच्चतम और फलन का एक निरपेक्ष निम्नतम हो सकता है। फलन के निरपेक्ष उच्चतम और निम्नतम  को फलन का सार्वत्रिक उच्चतम और सार्वत्रिक निम्नतम भी कहा जा सकता है।
-नीचे दी गई छवि में, बिंदु x = a फ़ंक्शन का निरपेक्ष मैक्सिमा है और x = b पर फ़ंक्शन का निरपेक्ष मिनिमा है।
+निरपेक्ष '''उच्चतम''' : एक बिंदु <math>x = a f(x)</math> के लिए सार्वत्रिक उच्चतम का बिंदु है यदि सभी <math>x\in D, (f(x)</math> का प्रांत <math>)</math> के लिए <math>f(x) \leq f(a)</math>है।
-== किसी फ़ंक्शन का मैक्सिमा और मिनिमा कैसे पता करें? ==
+'''निरपेक्ष निम्नतम''': एक बिंदु <math>x = a f(x)</math> के लिए सार्वत्रिक निम्नतम का बिंदु है यदि सभी <math>x\in D, (f(x)</math>का प्रांत <math>)</math> के लिए <math>f(x) \geq f(a)</math> है।
-फ़ंक्शन का मैक्सिमा और मिनिमा पहले-क्रम व्युत्पन्न परीक्षण और दूसरे-क्रम व्युत्पन्न परीक्षण का उपयोग करके गणना की जा सकती है। व्युत्पन्न परीक्षण किसी फ़ंक्शन का मैक्सिमा और मिनिमा खोजने का सबसे तेज़ तरीका है। आइए हम उन पर एक-एक करके चर्चा करें।
-== मैक्सिमा और मिनिमा के लिए प्रथम क्रम व्युत्पन्न परीक्षण ==
+नीचे दी गई छवि में, बिंदु <math>x = a</math> फलन का निरपेक्ष उच्चतम है और <math>x = b</math> पर फलन का निरपेक्ष निम्नतम है।
-किसी फ़ंक्शन का पहला व्युत्पन्न फ़ंक्शन का ढलान देता है। अधिकतम बिंदु के पास, वक्र का ढलान बढ़ता है क्योंकि हम अधिकतम बिंदु की ओर बढ़ते हैं फिर अधिकतम बिंदु पर 0 हो जाता है और फिर अधिकतम बिंदु से दूर जाने पर घटता है। इसी तरह, न्यूनतम बिंदु के पास, फ़ंक्शन का ढलान घटता है क्योंकि हम न्यूनतम बिंदु की ओर बढ़ते हैं फिर न्यूनतम बिंदु पर 0 हो जाता है और फिर न्यूनतम बिंदु से दूर जाने पर बढ़ता है। हम इस जानकारी का उपयोग यह जानने के लिए करते हैं कि बिंदु अधिकतम है या न्यूनतम।
-मान लें कि हमारे पास एक फ़ंक्शन f है जो एक खुले अंतराल I में परिभाषित महत्वपूर्ण बिंदु पर निरंतर है और f’(c) = 0 (ढलान c पर 0 है)। फिर हम वक्र के बाईं ओर और वक्र के दाईं ओर बिंदु पर f'(x) का मान जाँचते हैं और f'(x) की प्रकृति की जाँच करते हैं, फिर हम कह सकते हैं कि दिया गया बिंदु होगा:
+== किसी फलन का उच्चतम और निम्नतम ज्ञात करने की विधि ==
+फलन का उच्चतम और निम्नतम  पहले-कोटी  [[अवकलनीयता|अवकलन]] परीक्षण और दूसरे-कोटी  अवकलन परीक्षण का उपयोग करके गणना की जा सकती है। अवकलन परीक्षण किसी फलन का उच्चतम और निम्नतम  खोजने का सबसे तेज़ तरीका है। आइए हम उन पर एक-एक करके चर्चा करें।
-स्थानीय उच्चिष्ठ: यदि बिंदु c से x बढ़ने पर f’(x) का चिह्न धनात्मक से ऋणात्मक में बदल जाता है, तो f(c) उस श्रेणी में फ़ंक्शन का अधिकतम मान देता है।
+=== उच्चतम और निम्नतम के लिए, प्रथम कोटी अवकलन परीक्षण ===
+किसी फलन का पहला अवकलन फलन का ढलान देता है। अधिकतम बिंदु के पास, वक्र का ढलान बढ़ता है क्योंकि हम अधिकतम बिंदु की ओर बढ़ते हैं फिर अधिकतम बिंदु पर <math>0</math> हो जाता है और फिर अधिकतम बिंदु से दूर जाने पर घटता है। इसी तरह, न्यूनतम बिंदु के पास, फलन का ढलान घटता है क्योंकि हम न्यूनतम बिंदु की ओर बढ़ते हैं फिर न्यूनतम बिंदु पर <math>0</math> हो जाता है और फिर न्यूनतम बिंदु से दूर जाने पर बढ़ता है। हम इस जानकारी का उपयोग यह जानने के लिए करते हैं कि बिंदु अधिकतम है या न्यूनतम।
-स्थानीय निम्निष्ठ: यदि बिंदु c से x बढ़ने पर f’(x) का चिह्न ऋणात्मक से धनात्मक में बदल जाता है, तो f(c) उस श्रेणी में फ़ंक्शन का न्यूनतम मान देता है।
+मान लें कि हमारे पास एक फलन <math>f</math> है जो एक खुले अंतराल <math>I</math> में परिभाषित  छिद्रान्वेषी बिंदु पर निरंतर है और <math>f'(c) = 0</math> (ढलान <math>c</math> पर <math>0</math> है)। फिर हम वक्र के बाईं ओर और वक्र के दाईं ओर बिंदु पर <math>f'(x)</math> का मान जाँचते हैं और <math>f'(x)</math> की प्रकृति की जाँच करते हैं, फिर हम कह सकते हैं कि दिया गया बिंदु होगा:
-विभक्ति बिंदु: यदि c से x बढ़ने पर f’(x) का चिह्न नहीं बदलता है, और बिंदु c फ़ंक्शन का न तो उच्चिष्ठ है और न ही निम्निष्ठ, तो बिंदु c को विभक्ति बिंदु कहा जाता है।
+* '''स्थानीय उच्चतम'''  : यदि बिंदु <math>c</math> से <math>x</math> बढ़ने पर <math>f'(x)</math> का चिह्न धनात्मक से ऋणात्मक में बदल जाता है, तो <math>f(c)</math> उस श्रेणी में फलन का अधिकतम मान देता है।
+* '''स्थानीय निम्नतम''' : यदि बिंदु <math>c</math> से <math>x</math> बढ़ने पर <math>f'(x)</math> का चिह्न ऋणात्मक से धनात्मक में बदल जाता है, तो <math>f(c)</math> उस श्रेणी में फलन का न्यूनतम मान देता है।
+* '''परिवर्तन बिंदु''': यदि <math>c</math> से <math>x</math> बढ़ने पर <math>f'(x)</math> का चिह्न नहीं बदलता है, और बिंदु <math>c</math> फलन का न तो उच्चतम   है और न ही निम्नतम , तो बिंदु <math>c</math> को विभक्ति बिंदु कहा जाता है।
-== मैक्सिमा और मिनिमा के लिए द्वितीय-क्रम व्युत्पन्न परीक्षण ==
+=== उच्चतम और निम्नतम के लिए, द्वितीय कोटी  अवकलन परीक्षण ===
-मैक्सिमा और मिनिमा के लिए द्वितीय-क्रम व्युत्पन्न परीक्षण में, हम फ़ंक्शन का पहला व्युत्पन्न पाते हैं और यदि यह महत्वपूर्ण बिंदु x = c (f’(c) = 0) पर ढलान का मान 0 के बराबर देता है, तो हम फ़ंक्शन का दूसरा व्युत्पन्न पाते हैं। यदि फ़ंक्शन का दूसरा व्युत्पन्न दी गई सीमा के भीतर मौजूद है, तो दिया गया बिंदु होगा:
+उच्चतम और निम्नतम  के लिए द्वितीय-कोटी अवकलन परीक्षण में, हम फलन का पहला अवकलन पाते हैं और यदि यह  छिद्रान्वेषी बिंदु <math>x = c (f'(c) = 0)</math> पर ढलान का मान <math>0</math> के बराबर देता है, तो हम फलन का दूसरा अवकलन पाते हैं। यदि फलन का दूसरा अवकलन दी गई सीमा के भीतर उपस्थित है, तो दिया गया बिंदु निमलिखित प्रकार होगा:
-* '''Local maxima:''' If f<nowiki>''</nowiki>(c) < 0
+* '''स्थानीय अधिकतम:'''  यदि  <math>f''(c) < 0</math>
-* '''Local minima:''' If f<nowiki>''</nowiki>(c) > 0
+* '''स्थानीय न्यूनतम:'''  यदि <math>f''(c) > 0</math>
-* '''Test fails:''' If f<nowiki>''</nowiki>(c) = 0
+* '''परीक्षण विफल:'''  यदि  <math>f''(c) = 0</math>
-== मैक्सिमा और मिनिमा पर महत्वपूर्ण नोट्स: ==
+== महत्वपूर्ण टिप्पणियाँ ==
-मैक्सिमा और मिनिमा किसी फ़ंक्शन के वक्र में चोटियाँ और घाटियाँ हैं।
-किसी फ़ंक्शन का केवल एक निरपेक्ष मैक्सिमा और पूरे डोमेन पर फ़ंक्शन का एक निरपेक्ष मिनिमा हो सकता है।
+* उच्चतम और निम्नतम  किसी फलन के वक्र में चोटियाँ और घाटियाँ हैं।
+* किसी फलन का केवल एक निरपेक्ष उच्चतम और पूरे प्रांत पर फलन का एक निरपेक्ष निम्नतम हो सकता है।
+* अंतराल <math>I</math> में फलन <math>f</math> को एक एकदिष्ट (मोनोटोनॉस)फलन कहा जाता है, यदि <math>f</math> या तो <math>I</math> में बढ़ रहा है या <math>I</math> में घट रहा है।
-अंतराल I में फ़ंक्शन f को एक नीरस फ़ंक्शन कहा जाता है, यदि f या तो I में बढ़ रहा है या I में घट रहा है।
 [[Category:अवकलज के अनुप्रयोग]][[Category:गणित]][[Category:कक्षा-12]]