समाकलन की विधियाँ: Difference between revisions
(formulas) |
(added content) |
||
| Line 1: | Line 1: | ||
समाकलन, एक संपूर्ण को ज्ञात करने के लिए भाग को एकजुट करने का एक उपाय है। समाकलन कलन में, हम एक ऐसा फलन पाते हैं जिसका अंतर दिया गया है। इस प्रकार समाकलन अवकलन का प्रतिलोम है। समाकलन का उपयोग फलन के आलेख द्वारा परिबद्ध क्षेत्र के क्षेत्र को परिभाषित करने और गणना करने के लिए किया जाता है। वक्र आकार का क्षेत्र इसमें अंकित बहुभुज की भुजाओं की संख्या को ज्ञात कर अनुमानित किया जाता है। निःशेषण(क्सहॉशन) की विधि के रूप में जानी जाने वाली इस प्रक्रिया को बाद में समाकलन के रूप में अपनाया गया। | समाकलन, एक संपूर्ण को ज्ञात करने के लिए भाग को एकजुट करने का एक उपाय है। समाकलन कलन में, हम एक ऐसा फलन पाते हैं जिसका अंतर दिया गया है। इस प्रकार समाकलन अवकलन का प्रतिलोम है। समाकलन का उपयोग फलन के आलेख द्वारा परिबद्ध क्षेत्र के क्षेत्र को परिभाषित करने और गणना करने के लिए किया जाता है। वक्र आकार का क्षेत्र इसमें अंकित बहुभुज की भुजाओं की संख्या को ज्ञात कर अनुमानित किया जाता है। निःशेषण(क्सहॉशन) की विधि के रूप में जानी जाने वाली इस प्रक्रिया को बाद में समाकलन के रूप में अपनाया गया। | ||
== परिचय == | |||
हम समाकल के दो रूप प्राप्त करते हैं, '''अनिश्चित''' और '''निश्चित''' समाकल। अवकलन और समाकलन कलन में मौलिक उपकरण हैं जिनका उपयोग गणित और भौतिकी में समस्याओं को हल करने के लिए किया जाता है। समाकलन के सिद्धांत लाइबनिज द्वारा तैयार किए गए थे। आइए आगे बढ़ते हैं और समाकलन , इसके गुणों और इसकी कुछ शक्तिशाली तकनीकों के बारे में सीखते हैं। | हम समाकल के दो रूप प्राप्त करते हैं, '''अनिश्चित''' और '''निश्चित''' समाकल। अवकलन और समाकलन कलन में मौलिक उपकरण हैं जिनका उपयोग गणित और भौतिकी में समस्याओं को हल करने के लिए किया जाता है। समाकलन के सिद्धांत लाइबनिज द्वारा तैयार किए गए थे। आइए आगे बढ़ते हैं और समाकलन , इसके गुणों और इसकी कुछ शक्तिशाली तकनीकों के बारे में सीखते हैं। | ||
| Line 64: | Line 64: | ||
=== विधि 3: आंशिक भिन्नों का उपयोग करके समाकलन === | === विधि 3: आंशिक भिन्नों का उपयोग करके समाकलन === | ||
मान लीजिए हमें y= | मान लीजिए हमें <math>y={P(x) \over Q(x)}dx</math> ज्ञात करना है, जहाँ <math>{P(x) \over Q(x)}</math> एक अनुचित परिमेय फलन है। हम इसे इस तरह से घटाते हैं कि <math>{P(x) \over Q(x)}=T(x)+ {P_1(x) \over Q(x)}</math> । यहाँ, <math>T(x)</math>, <math>x</math> में बहुपद है और <math>{P_1(x) \over Q(x)}</math> उचित परिमेय फलन है। | ||
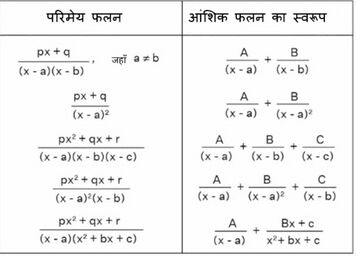
निम्न तालिका कुछ परिमेय फलनों और आंशिक भिन्नों के उनके संगत रूप को दर्शाती है।[[File:आंशिक भिन्नों द्वारा समाकलन.jpg|thumb|356x356px|आंशिक भिन्नों द्वारा समाकलन]] | |||
उदाहरण के लिए, आइए इसका समाकल ज्ञात करें | |||
f(x)=1(x+1)(x+2) using integration by partial fractions. | |||
By using partial fraction we have 1(x+1)(x+2)=Ax+1+Bx+2⋯(1). | |||
We will determine the values of A and B. | |||
On comparing in equation (1), we get 1=A(x+2)+B(x+1). | |||
From this, we have a set of two linear equations. | |||
A+B=0 and 2A+B =1 | |||
On solving these equations we get, A=1 and B=-1. | |||
So, equation (1) can be written as 1(x+1)(x+2)=1x+1−1x+2. | |||
Now, solving the integral | |||
∫(1(x+1)(x+2))dx=∫(1x+1−1x+2)dx=log|x+1|−log|x+2|+C=log∣∣∣x+1x+2∣∣∣+C | |||
=== Method 4: Integration by Parts === | === Method 4: Integration by Parts === | ||
Revision as of 21:58, 4 December 2024
समाकलन, एक संपूर्ण को ज्ञात करने के लिए भाग को एकजुट करने का एक उपाय है। समाकलन कलन में, हम एक ऐसा फलन पाते हैं जिसका अंतर दिया गया है। इस प्रकार समाकलन अवकलन का प्रतिलोम है। समाकलन का उपयोग फलन के आलेख द्वारा परिबद्ध क्षेत्र के क्षेत्र को परिभाषित करने और गणना करने के लिए किया जाता है। वक्र आकार का क्षेत्र इसमें अंकित बहुभुज की भुजाओं की संख्या को ज्ञात कर अनुमानित किया जाता है। निःशेषण(क्सहॉशन) की विधि के रूप में जानी जाने वाली इस प्रक्रिया को बाद में समाकलन के रूप में अपनाया गया।
परिचय
हम समाकल के दो रूप प्राप्त करते हैं, अनिश्चित और निश्चित समाकल। अवकलन और समाकलन कलन में मौलिक उपकरण हैं जिनका उपयोग गणित और भौतिकी में समस्याओं को हल करने के लिए किया जाता है। समाकलन के सिद्धांत लाइबनिज द्वारा तैयार किए गए थे। आइए आगे बढ़ते हैं और समाकलन , इसके गुणों और इसकी कुछ शक्तिशाली तकनीकों के बारे में सीखते हैं।
समाकलन वक्र के नीचे के क्षेत्र का क्षेत्रफल ज्ञात करने की प्रक्रिया है। यह क्षेत्र को आवरण करने वाले जितने भी छोटे आयत हों, उन्हें खींचकर और उनके क्षेत्रों को जोड़कर किया जाता है। योग एक सीमा के निकट पहुंचता है जो फलन के वक्र के नीचे के क्षेत्र के समान होता है। समाकलन फलन के प्रति अवकलज को ज्ञात करने की प्रक्रिया है। यदि कोई फलन समाकलनीय है और यदि प्रांत पर उसका समाकलन परिमित है, जिसकी सीमाएँ निर्दिष्ट हैं, तो यह निश्चित समाकलन है।
समाकलन के उपाय
कभी-कभी, कुछ फलन का इंटीग्रल ज्ञात करने के लिए निरीक्षण पर्याप्त नहीं होता है। इसके इंटीग्रल को ज्ञात करने के लिए मानक रूप में फलन को कम करने के लिए अतिरिक्त तरीके हैं। प्रमुख तरीकों पर नीचे चर्चा की गई है।
समाकलन के तरीके हैं:
- अपघटित विधि
- प्रतिस्थापन द्वारा समाकलन
- आंशिक भिन्नों द्वारा समाकलन
- खंडशः समाकलन
विधि 1: अपघटित विधि द्वारा समाकलन
फलन को ऐसे फलन के योग या अंतर में अपघटित किया जा सकता है, जिनके व्यक्तिगत समाकलन ज्ञात हैं। दिया गया समाकलन बीजीय, त्रिकोणमितीय या घातांकीय या इन फलनों का संयोजन होगा।
मान लीजिए हमें को एकीकृत करने की आवश्यकता है, तो हम फलन को इस प्रकार अपघटित करते हैं:
व्युत्क्रम नियम और घात नियम लागू करने पर, हम प्राप्त होता हैं
विधि 2: प्रतिस्थापन द्वारा समाकलन
प्रतिस्थापन द्वारा समाकलन विधि हमें समाकलन के चर को बदलने देती है ताकि समाकलन को आसान तरीके से एकीकृत किया जा सके।
मान लीजिए, हमें ज्ञात करना है।
मान लीजिए । फिर,
तो, को के रूप में लिखा जा सकता है।
उदाहरण के लिए, प्रतिस्थापन का उपयोग करके का समाकल ज्ञात करें।
मान लीजिए । फिर,
को के रूप में लिखा जा सकता है
ध्यान दें: समाकलन के चर के प्रतिस्थापन में त्रिकोणमितीय पहचान का भी उपयोग किया जा सकता है। कुछ महत्वपूर्ण मानक परिणाम इस प्रकार हैं:
विधि 3: आंशिक भिन्नों का उपयोग करके समाकलन
मान लीजिए हमें ज्ञात करना है, जहाँ एक अनुचित परिमेय फलन है। हम इसे इस तरह से घटाते हैं कि । यहाँ, , में बहुपद है और उचित परिमेय फलन है।
निम्न तालिका कुछ परिमेय फलनों और आंशिक भिन्नों के उनके संगत रूप को दर्शाती है।
उदाहरण के लिए, आइए इसका समाकल ज्ञात करें
f(x)=1(x+1)(x+2) using integration by partial fractions.
By using partial fraction we have 1(x+1)(x+2)=Ax+1+Bx+2⋯(1).
We will determine the values of A and B.
On comparing in equation (1), we get 1=A(x+2)+B(x+1).
From this, we have a set of two linear equations.
A+B=0 and 2A+B =1
On solving these equations we get, A=1 and B=-1.
So, equation (1) can be written as 1(x+1)(x+2)=1x+1−1x+2.
Now, solving the integral
∫(1(x+1)(x+2))dx=∫(1x+1−1x+2)dx=log|x+1|−log|x+2|+C=log∣∣∣x+1x+2∣∣∣+C
Method 4: Integration by Parts
This Integration rule is used to find the integral of two functions.
By product rule of derivatives, we have ddx(uv)=udvdx+vdudx⋯(1)
Integration on both sides of equation (1), we get ∫udvdxdx=uv−∫vdudxdx⋯(2)
Equation (2) can be written as uv=∫udvdxdx+∫vdudxdx
Let u=f(x) and dvdx=g(x).
Then, we have dudx=f′(x) and v = ∫ g(x)dx.
So, Equation (2) becomes
∫f(x)g(x)dx=f(x)∫g(x)dx−∫[f′(x)∫g(x)dx]dx
For example, let's find the integral of xex using integration by parts.
∫xexdx=x∫exdx−∫(dxdx∫exdx]dx=xex−∫[ex)dx=xex−ex+C
A few important standard results(Bernoulli's formula):
- ∫ eax sin bx dx = eax /(a2 + b2)[a sin bx - b cos bx] + C
- ∫ eax cos bx dx = eax /(a2 + b2)[a cos bx + b sin bx] + C