खंडशः समाकलन: Difference between revisions
(New Page Created) |
(formulas) |
||
| (10 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
कलन में खंडशः द्वारा समाकलन का विचार 1715 में ब्रूक टेलर द्वारा प्रस्तावित किया गया था, जिन्होंने प्रसिद्ध टेलर के प्रमेय का भी प्रस्ताव रखा था। साधारणतः, समाकलन की गणना उन फलनों के लिए की जाती है जिनके लिए अवकलन सूत्र उपस्थित होते हैं। यहाँ खंडशः द्वारा समाकलन एक अतिरिक्त तकनीक है जिसका उपयोग फलनों के गुणनफल के समाकलन को ज्ञात करने के लिए किया जाता है और इसे [[आंशिक भिन्नों द्वारा समाकलन|आंशिक]] समाकलन भी कहा जाता है। यह फलनों के गुणनफल के समाकलन को ऐसे समाकलनों में बदल देता है जिनके लिए समाधान की गणना आसानी से की जा सकती है। | |||
[[Category:गणित]] | |||
[[Category: | कुछ प्रतिलोम [[त्रिकोणमितीय फलनों की सीमाएं|त्रिकोणमितीय फलनों]] और लघुगणकीय फलनों में समाकलन सूत्र नहीं होते हैं, और यहाँ हम खंडशः द्वारा समाकलन सूत्र का उपयोग कर सकते हैं जिसे लोकप्रिय रूप से यूवी समाकलन सूत्र के रूप में भी जाना जाता है। यहाँ हम खंडशः द्वारा समाकलन की अवकलन , आलेखिय प्रतिनिधित्व, अनुप्रयोग और उदाहरणों की जाँच करेंगे। | ||
== परिभाषा == | |||
खंडशः द्वारा समाकलन का उपयोग दो या अधिक फलनों के गुणनफल को समाकलन करने के लिए किया जाता है। समाकलन किए जाने वाले दो फलन <math>f(x)</math> और <math>g(x)</math> , <math>\int f(x)\cdot g(x)</math> के रूप के हैं। इस प्रकार, इसे समाकलन का गुणन नियम कहा जा सकता है। दो फलनों में से, पहला फलन <math>f(x)</math> इस तरह से चुना जाता है कि उसका अवकलन सूत्र उपस्थित हो, और दूसरा फलन <math>g(x)</math> इस तरह से चुना जाता है कि ऐसे फलन का एक समाकल उपस्थित हो। | |||
<math>\int f(x)\cdot g(x)\cdot dx = f(x) \int g(x)\cdot dx - \int [(f'(x) \int g(x)\cdot dx)\cdot dx] + C</math> | |||
(प्रथम फलन <math>x </math> द्वितीय फलन ) का समाकलन = (प्रथम फलन ) <math>\times</math> (द्वितीय फलन का समाकलन ) - (प्रथम फलन का अवकलन x द्वितीय फलन का समाकलन ) का समाकलन । | |||
खंडशः द्वारा समाकलन में, सूत्र को दो खंडशः में विभाजित किया जाता है और हम दूसरे भाग में पहले फलन <math>f(x)</math> का अवकलन और दोनों खंडशः में दूसरे फलन <math>g(x)</math> का समाकलन देख सकते हैं। सरलता के लिए, इन फलन को प्रायः क्रमशः '<math>u</math>' और '<math>dv</math>' के रूप में दर्शाया जाता है। '<math>u</math>' और '<math>dv</math>' के संकेतन का उपयोग करके <math>uv</math> समाकलन सूत्र है: | |||
<math>\int u\ dv = uv - \int v \ du</math> | |||
== खंडशः समाकलन सूत्र == | |||
खंडशः द्वारा समाकलन सूत्र का उपयोग दो अलग-अलग प्रकार के फलनों जैसे लघुगणक, प्रतिलोम त्रिकोणमितीय, बीजीय, त्रिकोणमितीय और घातांकीय फलनों के गुणनफल का समाकल ज्ञात करने के लिए किया जाता है। खंडशः द्वारा समाकलन सूत्र का उपयोग किसी गुणनफल का समाकल ज्ञात करने के लिए किया जाता है। अवकलन के गुणनफल नियम में जहाँ हम किसी गुणनफल का अवकलन करते हैं, <math>uv, u(x),</math>और <math>v(x)</math> को किसी भी क्रम में चुना जा सकता है। लेकिन खंडशः द्वारा समाकलन सूत्र का उपयोग करते समय, पहला फलन <math>u(x)</math>चुनने के लिए, हमें यह देखना होगा कि निम्नलिखित में से कौन सा फलन निम्नलिखित क्रम में पहले आता है और फिर इसे <math>u</math> मान लें। | |||
इसे <math>LIATE</math> नियम का उपयोग करके याद किया जा सकता है। ध्यान दें कि यह क्रम <math>ILATE</math> सूत्र भी हो सकता है। उदाहरण के लिए, यदि हमें<math>\int \ln \ x\ dx</math> (जहाँ <math>x</math> एक बीजीय फलन है और <math>\ln</math> एक लघुगणकीय फलन है) ज्ञात करना है, तो हम <math>\ln x</math> को <math>u(x)</math> के रूप में चुनेंगे क्योंकि <math>LIATE</math> में लघुगणकीय फलन बीजीय फलन से पहले आता है। खंडशः द्वारा समाकलन सूत्र को दो तरीकों से परिभाषित किया गया है। हम दो फलनों के गुणनफल को समाकलन करने के लिए उनमें से किसी का भी उपयोग कर सकते हैं। | |||
== खंडशः समाकलन सूत्र अवकलन == | |||
खंडशः द्वारा समाकलन का प्रमाण दो फलनों के गुणनफल के अवकलन के सूत्र से प्राप्त किया जा सकता है। इस प्रकार, खंडशः द्वारा समाकलन सूत्र को समाकलन के गुणनफल नियम के रूप में भी जाना जाता है। | |||
आइए अवकलन के गुणन नियम का उपयोग करके खंडशः द्वारा समाकलन सूत्र प्राप्त करें। दो फलन <math>u </math> और <math>v</math> पर विचार करें। मान लें कि उनका गुणनफल <math>y</math> है। यानी, <math>y = uv</math>। अवकलन के गुणन नियम को लागू करने पर, हमें यह मिलता है | |||
<math>d/dx (uv) = u (dv/dx) + v (du/dx)</math> | |||
इसे इस प्रकार लिखा जा सकता है: | |||
<math>u (dv/dx) = d/dx (uv) - v (du/dx)</math> | |||
<math>x </math> के सापेक्ष दोनों पक्षों को समाकलन करने पर, | |||
<math>\int u (dv/dx) (dx) = \int d/dx (uv) dx - \int v (du/dx) dx</math> | |||
पदों को रद्द करके, | |||
<math>\int u\ dv = uv - \int v\ du</math> | |||
अतः खंडशः द्वारा समाकलन का सूत्र प्राप्त हो जाता है। | |||
<math>x </math> के सापेक्ष दोनों पक्षों पर समाकलन करने पर, | |||
<math>\int u (dv/dx) (dx) = \int d/dx (uv) dx - \int v (du/dx) dx</math> | |||
पदों को रद्द करके, | |||
<math>\int u\ dv = uv - \int v\ du</math> | |||
इसलिए खंडशः द्वारा समाकलन सूत्र प्राप्त होता है। | |||
== खंडशः समाकलन को दृष्टिगत करना == | |||
[[File:खंडशः समाकलन का आलेख.jpg|thumb|खंडशः समाकलन का आलेख]] | |||
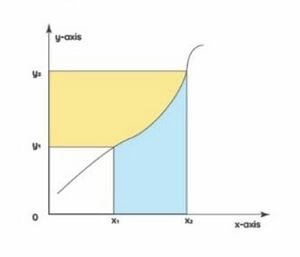
एक पैरामीट्रिक वक्र <math>(x, y) = (f(\theta), g(\theta))</math> पर विचार करें। आइए इस वक्र को समाकलनीय और एक-से-एक फलन मानें। भागों द्वारा समाकलन नीचे दिए गए वक्र से नीले क्षेत्र के क्षेत्र को दर्शाता है। आइए पहले नीले क्षेत्र और पीले क्षेत्रों के क्षेत्रों पर अलग-अलग विचार करें। | |||
<math>y </math>-अक्ष के साथ वक्र पर विचार करें, हमारे पास फलन <math>x(y)</math> है और सीमाओं <math>[y_1, y_2]</math>के पार है। इसके अलावा हम <math>x </math>-अक्ष के साथ वक्र पर विचार कर सकते हैं और सीमाओं <math>[x_1, x_2]</math> के पार फलन <math>y(x)</math> प्राप्त कर सकते हैं। | |||
पीले क्षेत्र का क्षेत्रफल <math>= \int_{}^{y_2} y_1 x(y)\cdot dy</math> | |||
नीले क्षेत्र का क्षेत्रफल <math>= \int_{}^{x_2} x_1 y(x)\cdot dx</math> | |||
इन दोनों क्षेत्रों का कुल क्षेत्रफल बड़े आयत के क्षेत्रफल में से छोटे आयत के क्षेत्रफल को घटाने के बराबर है। | |||
<math>\int_{}^{y_2} y_1 x(y)\cdot dy + \int_{}^{x_2}x_1 y(x)\cdot dx = [x\cdot y(x)]^{x_2}x_1</math> | |||
निश्चित समाकलनों के बिना इसे इस प्रकार लिखा जा सकता है। | |||
<math>\int y\cdot dx+ \int x\cdot dy = xy</math> | |||
<math>\int x\cdot dy = xy - \int y\cdot dx</math> | |||
इसके अलावा, खंडशः द्वारा समाकलन सूत्र प्राप्त करने के लिए इसे संशोधित किया जा सकता है। | |||
<math>\int f(x)\cdot g(x)\cdot dx = f(x)\cdot \int g(x)\cdot dx -\int (f'(x) \cdot \int g(x)\cdot dx) \cdot dx</math> | |||
== खंडशः समाकलन के अनुप्रयोग == | |||
खंडशः समाकलन के लिए इस सूत्र का अनुप्रयोग उन फलनों या व्यंजकों के लिए है जिनके लिए समाकलन के सूत्र उपस्थित नहीं हैं। यहाँ हम खंडशः द्वारा समाकलन के इस सूत्र को उपस्थित करने का प्रयास करते हैं और समाकलन निकालने का प्रयास करते हैं। लघुगणकीय फलनों और प्रतिलोम त्रिकोणमिति फलनों के लिए कोई समाकलन सूत्र नहीं हैं। आइए <math>\log x </math> और <math>tan^{-1}x</math> के समाकलन को हल करने और ज्ञात करने का प्रयास करें। | |||
== उदाहरण == | |||
'''उदाहरण:''' भागों द्वारा समाकलन सूत्र का उपयोग करके <math>x^2e^x</math> का समाकल ज्ञात करें। | |||
'''समाधान:''' | |||
<math>LIATE</math> का उपयोग करते हुए, <math>u = x^2 </math> और <math>dv = e^x dx </math> | |||
फिर, <math>du = 2x\ dx, v = \int e^x dx = e^x </math>। | |||
भागों द्वारा समाकलन के सूत्रों में से एक का उपयोग करते हुए, | |||
<math>\int u\ dv = uv -\int v du </math> | |||
<math>\int x^2 e^x dx = x^2 e^x - \int e^x (2x) dx </math> | |||
<math>= x^2 e^x - 2\int x\ e^x\ dx </math> | |||
मूल्यांकन करने के लिए भागों द्वारा समाकलन सूत्र को फिर से लागू करना <math>\int x \ e^x dx, </math> | |||
<math>\int x^2 e^x dx = x^2 e^x - 2 (x e^x - \int e^x dx) = x^2 e^x - 2 x e^x + 2 e^x + C </math> | |||
<math>= e^x (x^2- 2 x + 2)+ C </math> | |||
'''उत्तर:''' <math>\int x^2 e^x dx = = e^x (x^2- 2 x + 2)+ C </math> | |||
[[Category:समाकलन]][[Category:गणित]][[Category:कक्षा-12]] | |||
Latest revision as of 14:23, 6 December 2024
कलन में खंडशः द्वारा समाकलन का विचार 1715 में ब्रूक टेलर द्वारा प्रस्तावित किया गया था, जिन्होंने प्रसिद्ध टेलर के प्रमेय का भी प्रस्ताव रखा था। साधारणतः, समाकलन की गणना उन फलनों के लिए की जाती है जिनके लिए अवकलन सूत्र उपस्थित होते हैं। यहाँ खंडशः द्वारा समाकलन एक अतिरिक्त तकनीक है जिसका उपयोग फलनों के गुणनफल के समाकलन को ज्ञात करने के लिए किया जाता है और इसे आंशिक समाकलन भी कहा जाता है। यह फलनों के गुणनफल के समाकलन को ऐसे समाकलनों में बदल देता है जिनके लिए समाधान की गणना आसानी से की जा सकती है।
कुछ प्रतिलोम त्रिकोणमितीय फलनों और लघुगणकीय फलनों में समाकलन सूत्र नहीं होते हैं, और यहाँ हम खंडशः द्वारा समाकलन सूत्र का उपयोग कर सकते हैं जिसे लोकप्रिय रूप से यूवी समाकलन सूत्र के रूप में भी जाना जाता है। यहाँ हम खंडशः द्वारा समाकलन की अवकलन , आलेखिय प्रतिनिधित्व, अनुप्रयोग और उदाहरणों की जाँच करेंगे।
परिभाषा
खंडशः द्वारा समाकलन का उपयोग दो या अधिक फलनों के गुणनफल को समाकलन करने के लिए किया जाता है। समाकलन किए जाने वाले दो फलन और , के रूप के हैं। इस प्रकार, इसे समाकलन का गुणन नियम कहा जा सकता है। दो फलनों में से, पहला फलन इस तरह से चुना जाता है कि उसका अवकलन सूत्र उपस्थित हो, और दूसरा फलन इस तरह से चुना जाता है कि ऐसे फलन का एक समाकल उपस्थित हो।
(प्रथम फलन द्वितीय फलन ) का समाकलन = (प्रथम फलन ) (द्वितीय फलन का समाकलन ) - (प्रथम फलन का अवकलन x द्वितीय फलन का समाकलन ) का समाकलन ।
खंडशः द्वारा समाकलन में, सूत्र को दो खंडशः में विभाजित किया जाता है और हम दूसरे भाग में पहले फलन का अवकलन और दोनों खंडशः में दूसरे फलन का समाकलन देख सकते हैं। सरलता के लिए, इन फलन को प्रायः क्रमशः '' और '' के रूप में दर्शाया जाता है। '' और '' के संकेतन का उपयोग करके समाकलन सूत्र है:
खंडशः समाकलन सूत्र
खंडशः द्वारा समाकलन सूत्र का उपयोग दो अलग-अलग प्रकार के फलनों जैसे लघुगणक, प्रतिलोम त्रिकोणमितीय, बीजीय, त्रिकोणमितीय और घातांकीय फलनों के गुणनफल का समाकल ज्ञात करने के लिए किया जाता है। खंडशः द्वारा समाकलन सूत्र का उपयोग किसी गुणनफल का समाकल ज्ञात करने के लिए किया जाता है। अवकलन के गुणनफल नियम में जहाँ हम किसी गुणनफल का अवकलन करते हैं, और को किसी भी क्रम में चुना जा सकता है। लेकिन खंडशः द्वारा समाकलन सूत्र का उपयोग करते समय, पहला फलन चुनने के लिए, हमें यह देखना होगा कि निम्नलिखित में से कौन सा फलन निम्नलिखित क्रम में पहले आता है और फिर इसे मान लें।
इसे नियम का उपयोग करके याद किया जा सकता है। ध्यान दें कि यह क्रम सूत्र भी हो सकता है। उदाहरण के लिए, यदि हमें (जहाँ एक बीजीय फलन है और एक लघुगणकीय फलन है) ज्ञात करना है, तो हम को के रूप में चुनेंगे क्योंकि में लघुगणकीय फलन बीजीय फलन से पहले आता है। खंडशः द्वारा समाकलन सूत्र को दो तरीकों से परिभाषित किया गया है। हम दो फलनों के गुणनफल को समाकलन करने के लिए उनमें से किसी का भी उपयोग कर सकते हैं।
खंडशः समाकलन सूत्र अवकलन
खंडशः द्वारा समाकलन का प्रमाण दो फलनों के गुणनफल के अवकलन के सूत्र से प्राप्त किया जा सकता है। इस प्रकार, खंडशः द्वारा समाकलन सूत्र को समाकलन के गुणनफल नियम के रूप में भी जाना जाता है।
आइए अवकलन के गुणन नियम का उपयोग करके खंडशः द्वारा समाकलन सूत्र प्राप्त करें। दो फलन और पर विचार करें। मान लें कि उनका गुणनफल है। यानी, । अवकलन के गुणन नियम को लागू करने पर, हमें यह मिलता है
इसे इस प्रकार लिखा जा सकता है:
के सापेक्ष दोनों पक्षों को समाकलन करने पर,
पदों को रद्द करके,
अतः खंडशः द्वारा समाकलन का सूत्र प्राप्त हो जाता है।
के सापेक्ष दोनों पक्षों पर समाकलन करने पर,
पदों को रद्द करके,
इसलिए खंडशः द्वारा समाकलन सूत्र प्राप्त होता है।
खंडशः समाकलन को दृष्टिगत करना
एक पैरामीट्रिक वक्र पर विचार करें। आइए इस वक्र को समाकलनीय और एक-से-एक फलन मानें। भागों द्वारा समाकलन नीचे दिए गए वक्र से नीले क्षेत्र के क्षेत्र को दर्शाता है। आइए पहले नीले क्षेत्र और पीले क्षेत्रों के क्षेत्रों पर अलग-अलग विचार करें।
-अक्ष के साथ वक्र पर विचार करें, हमारे पास फलन है और सीमाओं के पार है। इसके अलावा हम -अक्ष के साथ वक्र पर विचार कर सकते हैं और सीमाओं के पार फलन प्राप्त कर सकते हैं।
पीले क्षेत्र का क्षेत्रफल
नीले क्षेत्र का क्षेत्रफल
इन दोनों क्षेत्रों का कुल क्षेत्रफल बड़े आयत के क्षेत्रफल में से छोटे आयत के क्षेत्रफल को घटाने के बराबर है।
निश्चित समाकलनों के बिना इसे इस प्रकार लिखा जा सकता है।
इसके अलावा, खंडशः द्वारा समाकलन सूत्र प्राप्त करने के लिए इसे संशोधित किया जा सकता है।
खंडशः समाकलन के अनुप्रयोग
खंडशः समाकलन के लिए इस सूत्र का अनुप्रयोग उन फलनों या व्यंजकों के लिए है जिनके लिए समाकलन के सूत्र उपस्थित नहीं हैं। यहाँ हम खंडशः द्वारा समाकलन के इस सूत्र को उपस्थित करने का प्रयास करते हैं और समाकलन निकालने का प्रयास करते हैं। लघुगणकीय फलनों और प्रतिलोम त्रिकोणमिति फलनों के लिए कोई समाकलन सूत्र नहीं हैं। आइए और के समाकलन को हल करने और ज्ञात करने का प्रयास करें।
उदाहरण
उदाहरण: भागों द्वारा समाकलन सूत्र का उपयोग करके का समाकल ज्ञात करें।
समाधान:
का उपयोग करते हुए, और
फिर, ।
भागों द्वारा समाकलन के सूत्रों में से एक का उपयोग करते हुए,
मूल्यांकन करने के लिए भागों द्वारा समाकलन सूत्र को फिर से लागू करना
उत्तर: