दो वक्रों के मध्यवर्ती क्षेत्र का क्षेत्रफल: Difference between revisions
(formulas) |
(added internal links) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
दो वक्रों के मध्यवर्ती क्षेत्र ज्ञात करना समाकलन का एक आवश्यक अनुप्रयोग है। समाकलन का उपयोग करके, हमने वक्र के अंतर्गत क्षेत्र ज्ञात करना सीखा है, इसी तरह, हम समाकलन का उपयोग करके दो प्रतिच्छेद करने वाले वक्रों के मध्यवर्ती क्षेत्र भी ज्ञात कर सकते हैं। यह अंतरिक्ष का वह भाग है जो दी गई सीमाओं के भीतर दो रैखिक या गैर-रैखिक वक्रों के बीच आता है। | दो वक्रों के मध्यवर्ती क्षेत्र ज्ञात करना समाकलन का एक आवश्यक अनुप्रयोग है। [[समाकलन की विधियाँ|समाकलन]] का उपयोग करके, हमने वक्र के अंतर्गत क्षेत्र ज्ञात करना सीखा है, इसी तरह, हम समाकलन का उपयोग करके दो प्रतिच्छेद करने वाले वक्रों के मध्यवर्ती क्षेत्र भी ज्ञात कर सकते हैं। यह अंतरिक्ष का वह भाग है जो दी गई सीमाओं के भीतर दो रैखिक या गैर-रैखिक वक्रों के बीच आता है। | ||
दो वक्रों के मध्यवर्ती क्षेत्र मिश्रित भी हो सकता है, लेकिन समाकलन का उपयोग करके हम दो वक्रों के अंतर्गत क्षेत्र ज्ञात करने के लिए उपयोग किए जाने वाले ज्ञात सूत्रों में सरल संशोधन करके भी इसे आसानी से ज्ञात कर सकते हैं। | दो वक्रों के मध्यवर्ती क्षेत्र मिश्रित भी हो सकता है, लेकिन समाकलन का उपयोग करके हम दो [[साधारण वक्रों के अंतर्गत क्षेत्रफल|वक्रों के अंतर्गत क्षेत्र]] ज्ञात करने के लिए उपयोग किए जाने वाले ज्ञात सूत्रों में सरल संशोधन करके भी इसे आसानी से ज्ञात कर सकते हैं। | ||
[[File:दो वक्रों के मध्यवर्ती क्षेत्र का क्षेत्रफल.jpg|thumb|दो वक्रों के मध्यवर्ती क्षेत्र का क्षेत्रफल]] | |||
== परिचय == | == परिचय == | ||
दो वक्रों के मध्यवर्ती क्षेत्र, वह क्षेत्र होता है जो दो प्रतिच्छेदित वक्रों के बीच आता है और इसकी गणना समाकलन कलन (इंटीग्रल कैलकुलस) का उपयोग करके की जा सकती है। समाकलन का उपयोग दो वक्रों के नीचे के क्षेत्र को ज्ञात करने के लिए किया जा सकता है जहाँ हम दो वक्रों के समीकरण और उनके प्रतिच्छेद बिंदुओं को जानते हैं। यदि हम छवि में देखें, तो हमारे पास दो फलन | दो वक्रों के मध्यवर्ती क्षेत्र, वह क्षेत्र होता है जो दो प्रतिच्छेदित वक्रों के बीच आता है और इसकी गणना समाकलन कलन (इंटीग्रल कैलकुलस) का उपयोग करके की जा सकती है। समाकलन का उपयोग दो वक्रों के नीचे के क्षेत्र को ज्ञात करने के लिए किया जा सकता है जहाँ हम दो वक्रों के समीकरण और उनके प्रतिच्छेद बिंदुओं को जानते हैं। यदि हम छवि में देखें, तो हमारे पास दो फलन <math>f(x)</math>और <math>g(x)</math> हैं और हमें छायांकित भाग में दिए गए इन दो वक्रों के मध्यवर्ती क्षेत्र ज्ञात करना है। फिर समाकलन का उपयोग करके, हम आसानी से छायांकित भाग के क्षेत्र की गणना कर सकते हैं। आइए अगले भाग में इस क्षेत्र की गणना पर अधिक चर्चा करें। | ||
[[File:मध्यवर्ती क्षेत्रफल सूत्र.jpg|thumb|मध्यवर्ती क्षेत्रफल सूत्र]] | |||
== दो वक्रों के मध्यवर्ती क्षेत्रफल सूत्र == | == दो वक्रों के मध्यवर्ती क्षेत्रफल सूत्र == | ||
| Line 11: | Line 12: | ||
क्षेत्रफल <math>= \int_{a}^{b} [f(x)-g(x)]dx</math> | क्षेत्रफल <math>= \int_{a}^{b} [f(x)-g(x)]dx</math> | ||
[[File:Y के सापेक्ष दो वक्रों के मध्यवर्ती क्षेत्र.jpg|thumb|Y के सापेक्ष दो वक्रों के मध्यवर्ती क्षेत्र]] | |||
=== Y के सापेक्ष दो वक्रों के मध्यवर्ती क्षेत्र === | === Y के सापेक्ष दो वक्रों के मध्यवर्ती क्षेत्र === | ||
<math>y </math>-अक्ष के सापेक्ष दो वक्रों के मध्यवर्ती क्षेत्र उन वक्रों के क्षेत्रों की गणना करने की विधि है जिनका समीकरण <math>y </math> के संदर्भ में दिया गया है। <math>x </math>-अक्ष के साथ क्षेत्र की गणना करने की तुलना में <math>y </math>-अक्ष के साथ क्षेत्र की गणना करना आसान है। इस विधि में, हम दिए गए क्षेत्र को दी गई सीमाओं के बीच क्षैतिज पट्टियों में विभाजित करते हैं, और समाकलन का उपयोग करके, हम दो वक्रों के बीच अनुभाग का क्षेत्र ज्ञात करने के लिए क्षैतिज पट्टियों के क्षेत्रों को जोड़ते हैं। यदि <math>f(y)</math>और <math>g(y), [c, d]</math> पर सतत हैं और <math>[c, d]</math> में सभी <math>y </math> के लिए <math>g(y) < f(y)</math> है, तो | <math>y </math>-अक्ष के सापेक्ष दो वक्रों के मध्यवर्ती क्षेत्र उन वक्रों के क्षेत्रों की गणना करने की विधि है जिनका समीकरण <math>y </math> के संदर्भ में दिया गया है। <math>x </math>-अक्ष के साथ क्षेत्र की गणना करने की तुलना में <math>y </math>-अक्ष के साथ क्षेत्र की गणना करना आसान है। इस विधि में, हम दिए गए क्षेत्र को दी गई सीमाओं के बीच क्षैतिज पट्टियों में विभाजित करते हैं, और समाकलन का उपयोग करके, हम दो वक्रों के बीच अनुभाग का क्षेत्र ज्ञात करने के लिए क्षैतिज पट्टियों के क्षेत्रों को जोड़ते हैं। यदि <math>f(y)</math> और <math>g(y), [c, d]</math> पर सतत हैं और <math>[c, d]</math> में सभी <math>y </math> के लिए <math>g(y) < f(y)</math> है, तो | ||
क्षेत्रफल <math>= \int_{a}^{b} [f(y )-g(y )]dy </math> | क्षेत्रफल <math>= \int_{a}^{b} [f(y )-g(y )]dy </math> | ||
[[File:दो मिश्रित वक्रों के मध्यवर्ती क्षेत्र.jpg|thumb|दो मिश्रित वक्रों के मध्यवर्ती क्षेत्र]] | |||
=== दो मिश्रित वक्रों के मध्यवर्ती क्षेत्र === | === दो मिश्रित वक्रों के मध्यवर्ती क्षेत्र === | ||
ऊपर बताए गए सूत्रों का उपयोग करके एक दूसरे को प्रतिच्छेद करने वाले दो मिश्रित वक्रों के बीच के क्षेत्रों की गणना करने पर गलत परिणाम मिलेगा और प्रतिच्छेद के बाद वक्र अपना स्थान बदल लेंगे। छवि में दिखाए गए वक्रों के लिए, हमने अंतरालों को विभिन्न भागों में विभाजित किया और फिर प्रत्येक खंड में वक्रों के बीच अलग-अलग क्षेत्रों की गणना की। मान लें कि <math>f(x)</math> और <math>g(x)</math>, <math>[a, b]</math> अंतराल में सतत हैं, तो वक्रों के मध्यवर्ती क्षेत्र होगा: | ऊपर बताए गए सूत्रों का उपयोग करके एक दूसरे को प्रतिच्छेद करने वाले दो मिश्रित वक्रों के बीच के क्षेत्रों की गणना करने पर गलत परिणाम मिलेगा और प्रतिच्छेद के बाद वक्र अपना स्थान बदल लेंगे। छवि में दिखाए गए वक्रों के लिए, हमने अंतरालों को विभिन्न भागों में विभाजित किया और फिर प्रत्येक खंड में वक्रों के बीच अलग-अलग क्षेत्रों की गणना की। मान लें कि <math>f(x)</math> और <math>g(x)</math>, <math>[a, b]</math> अंतराल में सतत हैं, तो वक्रों के मध्यवर्ती क्षेत्र होगा: | ||
क्षेत्रफल <math>= \int_{a}^{c }\left\vert f(x)-g(x) \right\vert dx</math> | क्षेत्रफल <math>= \int_{a}^{c }\left\vert f(x)-g(x) \right\vert dx</math> | ||
जैसा कि हम क्षेत्र [a, b] में देखते हैं, <math>f(x) \geq g(x)</math> और क्षेत्र <math>[c, d]</math> में <math>g (x) \geq f (x)</math> , इसलिए हम सीमाओं को दो भागों में तोड़ते हैं: | |||
जैसा कि हम क्षेत्र [a, b] में देखते हैं, <math>f(x) \geq g(x)</math> और क्षेत्र <math>[c, d]</math> में <math>g (x) \geq f (x)</math> , इसलिए हम सीमाओं को दो भागों में तोड़ते हैं: | |||
क्षेत्रफल <math> = \int_{a}^{b} [f(x)-g(x)]dx + \int_{b }^{c } [g (x)-f (x)]dx</math> | क्षेत्रफल <math> = \int_{a}^{b} [f(x)-g(x)]dx + \int_{b }^{c } [g (x)-f (x)]dx</math> | ||
[[File:दो ध्रुवीय वक्रों के मध्यवर्ती क्षेत्र.jpg|thumb|दो ध्रुवीय वक्रों के मध्यवर्ती क्षेत्र]] | |||
=== दो ध्रुवीय वक्रों के मध्यवर्ती क्षेत्र === | === दो ध्रुवीय वक्रों के मध्यवर्ती क्षेत्र === | ||
समाकलन कलन का उपयोग करके हम दो ध्रुवीय वक्रों के बीच के क्षेत्र की गणना भी कर सकते हैं। जब हमारे पास दो वक्र होते हैं जिनके निर्देशांक आयताकार निर्देशांक में नहीं, बल्कि ध्रुवीय निर्देशांक में दिए जाते हैं, तो हम इस विधि का उपयोग करते हैं। हम इसे हल करने के लिए हमेशा ध्रुवीय को आयताकार निर्देशांक में भी बदल सकते हैं, लेकिन हम जटिलता को कम करने के लिए इस विधि का उपयोग कर सकते हैं। मान लें कि हमारे पास दो ध्रुवीय वक्र हैं <math>r_0= f(\theta)</math> और <math>r_i = g(\theta)</math> जैसा कि छवि में दिखाया गया है, और हम इन दो वक्रों के बीच संलग्न क्षेत्र को इस तरह से ज्ञात करना चाहते हैं कि <math>\alpha \leq \theta \leq \beta</math> जहाँ <math>[\alpha, \beta]</math> परिबद्ध क्षेत्र है। तब वक्रों के मध्यवर्ती क्षेत्र होगा: | |||
<math>A=\frac{1}{2}\int_{\alpha}^{\beta} (r^2_0-r^2_i)d\theta-</math> | <math>A=\frac{1}{2}\int_{\alpha}^{\beta} (r^2_0-r^2_i)d\theta-</math> | ||
== उदाहरण == | == उदाहरण == | ||
| Line 58: | Line 57: | ||
<math>= 1/12</math> | <math>= 1/12</math> | ||
'''उत्तर''': निम्नलिखित अंतराल के अंतर्गत दिए गए वक्रों के बीच का क्षेत्रफल 1/12 इकाई वर्ग है। | '''उत्तर''': निम्नलिखित अंतराल के अंतर्गत दिए गए वक्रों के बीच का क्षेत्रफल <math>1/12</math> इकाई वर्ग है। | ||
[[Category:समकलनों के अनुप्रयोग]] | [[Category:समकलनों के अनुप्रयोग]] | ||
[[Category:गणित]] | [[Category:गणित]] | ||
[[Category:कक्षा-12]] | [[Category:कक्षा-12]] | ||
Latest revision as of 11:07, 8 December 2024
दो वक्रों के मध्यवर्ती क्षेत्र ज्ञात करना समाकलन का एक आवश्यक अनुप्रयोग है। समाकलन का उपयोग करके, हमने वक्र के अंतर्गत क्षेत्र ज्ञात करना सीखा है, इसी तरह, हम समाकलन का उपयोग करके दो प्रतिच्छेद करने वाले वक्रों के मध्यवर्ती क्षेत्र भी ज्ञात कर सकते हैं। यह अंतरिक्ष का वह भाग है जो दी गई सीमाओं के भीतर दो रैखिक या गैर-रैखिक वक्रों के बीच आता है।
दो वक्रों के मध्यवर्ती क्षेत्र मिश्रित भी हो सकता है, लेकिन समाकलन का उपयोग करके हम दो वक्रों के अंतर्गत क्षेत्र ज्ञात करने के लिए उपयोग किए जाने वाले ज्ञात सूत्रों में सरल संशोधन करके भी इसे आसानी से ज्ञात कर सकते हैं।
परिचय
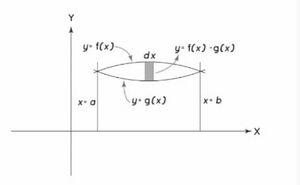
दो वक्रों के मध्यवर्ती क्षेत्र, वह क्षेत्र होता है जो दो प्रतिच्छेदित वक्रों के बीच आता है और इसकी गणना समाकलन कलन (इंटीग्रल कैलकुलस) का उपयोग करके की जा सकती है। समाकलन का उपयोग दो वक्रों के नीचे के क्षेत्र को ज्ञात करने के लिए किया जा सकता है जहाँ हम दो वक्रों के समीकरण और उनके प्रतिच्छेद बिंदुओं को जानते हैं। यदि हम छवि में देखें, तो हमारे पास दो फलन और हैं और हमें छायांकित भाग में दिए गए इन दो वक्रों के मध्यवर्ती क्षेत्र ज्ञात करना है। फिर समाकलन का उपयोग करके, हम आसानी से छायांकित भाग के क्षेत्र की गणना कर सकते हैं। आइए अगले भाग में इस क्षेत्र की गणना पर अधिक चर्चा करें।
दो वक्रों के मध्यवर्ती क्षेत्रफल सूत्र
यदि हम दो वक्रों के मध्यवर्ती क्षेत्रफल ज्ञात करना चाहते हैं, तो हमें क्षेत्र को से तक -अक्ष के समानांतर कई छोटी आयताकार पट्टियों में विभाजित करना होगा, और समाकलन का उपयोग करके हम दो वक्रों का अनुमानित क्षेत्रफल प्राप्त करने के लिए इन छोटी पट्टियों के क्षेत्रों को जोड़ सकते हैं। इन आयताकार पट्टियों की चौड़ाई "" और ऊँचाई होगी। छोटी आयताकार पट्टी का क्षेत्रफल है और अब और की सीमाओं के भीतर समाकलन का उपयोग करके, हम इन दो वक्रों के बीच के क्षेत्र की गणना कर सकते हैं। यदि और , पर सतत हैं और में सभी के लिए है, तो हमारे पास निम्न सूत्र है।
क्षेत्रफल
Y के सापेक्ष दो वक्रों के मध्यवर्ती क्षेत्र
-अक्ष के सापेक्ष दो वक्रों के मध्यवर्ती क्षेत्र उन वक्रों के क्षेत्रों की गणना करने की विधि है जिनका समीकरण के संदर्भ में दिया गया है। -अक्ष के साथ क्षेत्र की गणना करने की तुलना में -अक्ष के साथ क्षेत्र की गणना करना आसान है। इस विधि में, हम दिए गए क्षेत्र को दी गई सीमाओं के बीच क्षैतिज पट्टियों में विभाजित करते हैं, और समाकलन का उपयोग करके, हम दो वक्रों के बीच अनुभाग का क्षेत्र ज्ञात करने के लिए क्षैतिज पट्टियों के क्षेत्रों को जोड़ते हैं। यदि और पर सतत हैं और में सभी के लिए है, तो
क्षेत्रफल
दो मिश्रित वक्रों के मध्यवर्ती क्षेत्र
ऊपर बताए गए सूत्रों का उपयोग करके एक दूसरे को प्रतिच्छेद करने वाले दो मिश्रित वक्रों के बीच के क्षेत्रों की गणना करने पर गलत परिणाम मिलेगा और प्रतिच्छेद के बाद वक्र अपना स्थान बदल लेंगे। छवि में दिखाए गए वक्रों के लिए, हमने अंतरालों को विभिन्न भागों में विभाजित किया और फिर प्रत्येक खंड में वक्रों के बीच अलग-अलग क्षेत्रों की गणना की। मान लें कि और , अंतराल में सतत हैं, तो वक्रों के मध्यवर्ती क्षेत्र होगा:
क्षेत्रफल
जैसा कि हम क्षेत्र [a, b] में देखते हैं, और क्षेत्र में , इसलिए हम सीमाओं को दो भागों में तोड़ते हैं:
क्षेत्रफल
दो ध्रुवीय वक्रों के मध्यवर्ती क्षेत्र
समाकलन कलन का उपयोग करके हम दो ध्रुवीय वक्रों के बीच के क्षेत्र की गणना भी कर सकते हैं। जब हमारे पास दो वक्र होते हैं जिनके निर्देशांक आयताकार निर्देशांक में नहीं, बल्कि ध्रुवीय निर्देशांक में दिए जाते हैं, तो हम इस विधि का उपयोग करते हैं। हम इसे हल करने के लिए हमेशा ध्रुवीय को आयताकार निर्देशांक में भी बदल सकते हैं, लेकिन हम जटिलता को कम करने के लिए इस विधि का उपयोग कर सकते हैं। मान लें कि हमारे पास दो ध्रुवीय वक्र हैं और जैसा कि छवि में दिखाया गया है, और हम इन दो वक्रों के बीच संलग्न क्षेत्र को इस तरह से ज्ञात करना चाहते हैं कि जहाँ परिबद्ध क्षेत्र है। तब वक्रों के मध्यवर्ती क्षेत्र होगा:
उदाहरण
उदाहरण : दिए गए क्षेत्र में अंतराल के भीतर दो वक्रों और के बीच का क्षेत्रफल ज्ञात कीजिए, जहाँ है।
समाधान:
दिया गया: और
दो वक्रों के बीच के क्षेत्र के लिए सूत्र का उपयोग:
क्षेत्रफल
क्षेत्रफल
उत्तर: निम्नलिखित अंतराल के अंतर्गत दिए गए वक्रों के बीच का क्षेत्रफल इकाई वर्ग है।