स्थिति सदिश: Difference between revisions
No edit summary |
(added internal links) |
||
| (5 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
स्थिति सदिश का उपयोग हमें एक वस्तु के सापेक्ष दूसरी वस्तु का स्थान ज्ञात करने में सहायता करने के लिए किया जाता है। स्थिति सदिश साधारणतः मूल बिंदु से प्रारंभ होते हैं और फिर किसी अन्य मनमाने बिंदु पर समाप्त होते हैं। इस प्रकार, इन सदिशों का उपयोग किसी विशेष बिंदु की स्थिति को उसके मूल बिंदु के संदर्भ में निर्धारित करने के लिए किया जाता है। | |||
[[Category: | इस लेख में, आइए स्थिति सदिशों, उनकी परिभाषा, हल किए गए उदाहरणों के साथ सूत्रों के बारे में जानें। | ||
स्थिति सदिश एक सरल रेखा है जिसका एक छोर किसी पिंड से जुड़ा होता है और दूसरा छोर किसी गतिशील बिंदु से जुड़ा होता है और इसका उपयोग पिंड के सापेक्ष बिंदु की स्थिति का वर्णन करने के लिए किया जाता है। जैसे-जैसे बिंदु गति करता है, स्थिति सदिश लंबाई या दिशा में या लंबाई और दिशा दोनों में बदलेगा। | |||
== परिभाषा == | |||
स्थिति सदिश, को एक [[सदिशों का योगफल|सदिश]] के रूप में परिभाषित किया जाता है जो किसी भी मनमाने संदर्भ बिंदु जैसे मूल के संबंध में किसी भी दिए गए बिंदु की स्थिति या स्थान को इंगित करता है। स्थिति सदिश की दिशा सदैव उस सदिश के मूल से दिए गए बिंदु की ओर इंगित करती है। | |||
* [[कार्टेशियन पद्धति|कार्टेशियन]] निर्देशांक प्रणाली में, यदि <math>O</math> मूल बिंदु है और <math>P(x_1, y_1)</math> एक अन्य बिंदु है, तो बिंदु <math>O</math> से बिंदु <math>P</math> तक निर्देशित होने वाला स्थिति सदिश <math>OP</math> के रूप में दर्शाया जा सकता है। | |||
* त्रि-आयामी अंतरिक्ष में, यदि मूल बिंदु <math>O = (0,0,0)</math> और <math>P = (x_1, y_1, z_1)</math>है, तो बिंदु <math>P</math> का स्थिति सदिश v इस प्रकार दर्शाया जा सकता है: <math>v = x_1i + y_1j + z_1k</math> | |||
[[File:स्थिति सदिश.jpg|thumb|स्थिति सदिश]] | |||
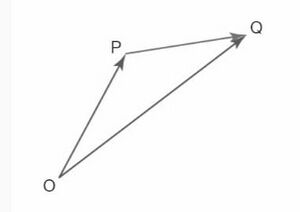
आइए दो सदिशों, <math>P</math> और <math>Q</math> पर विचार करें, जिनके स्थान सदिश क्रमशः <math>p = (2,4)</math> और <math>q = (3, 5)</math> हैं। सदिश <math>P</math> और <math>Q</math> के निर्देशांक इस प्रकार लिखे जा सकते हैं: <math>P = (2,4), Q = (3, 5)</math>। आइए नीचे दी गई छवि में दिखाए गए मूल बिंदु O पर विचार करें। हम एक कण पर विचार करेंगे जो बिंदु <math>P</math> से बिंदु <math>Q</math> तक गति करता है। किसी कण के स्थान सदिश को उस सदिश के रूप में परिभाषित किया जा सकता है जो मूल बिंदु से उस बिंदु तक प्रारंभ होता है जहाँ कण स्थित है। | |||
उपरोक्त चित्र में, जब कण बिंदु <math>P</math> पर होता है तो उसका स्थिति सदिश <math>OP</math> होता है और जब वह बिंदु <math>Q</math> पर होता है तो <math>OQ</math> होता है। | |||
== स्थिति सदिश कैसे ज्ञात करें? == | |||
किसी बिंदु का स्थिति सदिश ज्ञात करने से पहले, उसके निर्देशांक निर्धारित करना आवश्यक है। दो बिंदुओं, <math>A</math> और <math>B</math> पर विचार करें, जहाँ <math>A = (x_1, y_1)</math> और <math>B = (x_2, y_2)</math> है। | |||
इसके बाद, हम बिंदु <math>A</math> से बिंदु <math>B</math> तक स्थिति सदिश, सदिश AB ज्ञात करेंगे। | |||
इस स्थिति सदिश को निर्धारित करने के लिए, हमें <math>A</math> के संगत घटकों को <math>B</math> से घटाना होगा: <math>AB = (x_2 - x_1, y_2 - y_1) = (x_2 - x_1) i + (y_2 - y_1) j</math> | |||
== स्थिति सदिश सूत्र == | |||
यदि हम <math>xy</math>-तल में किसी बिंदु की स्थिति जानते हैं, तो हम उन दो बिंदुओं के बीच स्थिति सदिश निर्धारित करने के लिए सूत्र का उपयोग कर सकते हैं। उदाहरण के लिए, एक बिंदु <math>A</math> पर विचार करें, जिसके निर्देशांक <math>xy</math>-तल में <math>(x_k, y_k)</math> हैं, और दूसरा बिंदु <math>B</math>, जिसके निर्देशांक <math>(x_{k+1}, y_{k+1})</math> हैं। | |||
* <math>A</math> से <math>B</math> तक स्थिति सदिश निर्धारित करने का सूत्र <math>AB = (x_{k+1} - x_k, y_{k+1} - y_k)</math> है। | |||
* स्थिति सदिश <math>AB</math> एक सदिश को संदर्भित करता है जो बिंदु <math>A</math> से प्रारंभ होता है और बिंदु <math>B</math> पर समाप्त होता है। | |||
* इसी तरह, यदि हम बिंदु <math>B</math> से बिंदु <math>A</math> तक स्थिति सदिश ज्ञात करना चाहते हैं, तो हम इसका उपयोग कर सकते हैं: <math>BA = (x_k - x_{k+1}, y_k - y_{k+1})</math> | |||
== उदाहरण == | |||
'''उदाहरण:''' दो बिंदु <math>P = (-4, 6)</math> और <math>Q = (5, 11)</math> दिए होने पर स्थिति सदिश <math>QP</math> निर्धारित करें। | |||
समाधान: यदि <math>xy</math>-निर्देशांक प्रणाली में दो बिंदु दिए गए हैं, तो हम स्थिति सदिश <math>QP</math> ज्ञात करने के लिए निम्नलिखित सूत्र का उपयोग कर सकते हैं: | |||
<math>QP = (x_1 - x_2, y_1 - y_2)</math> | |||
जहाँ <math>(x_1, y_1)</math> बिंदु <math>P</math> के निर्देशांकों को दर्शाता है और <math>(x_2, y_2)</math> बिंदु <math>Q</math> के निर्देशांकों को दर्शाता है। ध्यान दें कि स्थिति सदिश <math>QP</math> बिंदु <math>Q</math> से बिंदु <math>P</math> की ओर निर्देशित एक सदिश को दर्शाता है। यह स्थिति सदिश <math>PQ</math> से भिन्न है, जो <math>P</math> से <math>Q</math> की ओर निर्देशित होता है। इस प्रकार, उपरोक्त समीकरण में केवल बिंदु <math>P</math> और <math>Q</math> के मान डालकर, हम स्थिति सदिश <math>QP</math> ज्ञात कर सकते हैं: | |||
<math>QP = (-4-5, 6-11)</math> | |||
<math>QP = (-9, -5) = -9 i - 5 j</math> | |||
इस प्रकार, स्थिति सदिश <math>QP</math> मूल बिंदु से प्रारंभ होने वाले सदिश के बराबर है। यह सदिश 9 इकाइयों के बिंदु पर निर्देशित होता है जो <math>x</math>-अक्ष के साथ बाईं ओर और <math>y</math>-अक्ष के साथ 5 इकाइयों नीचे की ओर होता है। | |||
== महत्वपूर्ण टिप्पणियाँ == | |||
यहाँ कुछ बिंदुओं की सूची दी गई है जिन्हें स्थिति सदिश का अध्ययन करते समय याद रखना चाहिए | |||
* स्थिति सदिश को एक सदिश के रूप में परिभाषित किया जाता है जो मूल बिंदु जैसे किसी भी मनमाने संदर्भ बिंदु के संबंध में किसी दिए गए बिंदु की स्थिति या स्थान को इंगित करता है। | |||
* स्थिति सदिश की दिशा सदैव उस सदिश के मूल बिंदु से दिए गए बिंदु की ओर इंगित करती है। | |||
[[Category:गणित]][[Category:कक्षा-12]] | |||
[[Category:सदिश बीजगणित]] | |||
Latest revision as of 09:50, 15 December 2024
स्थिति सदिश का उपयोग हमें एक वस्तु के सापेक्ष दूसरी वस्तु का स्थान ज्ञात करने में सहायता करने के लिए किया जाता है। स्थिति सदिश साधारणतः मूल बिंदु से प्रारंभ होते हैं और फिर किसी अन्य मनमाने बिंदु पर समाप्त होते हैं। इस प्रकार, इन सदिशों का उपयोग किसी विशेष बिंदु की स्थिति को उसके मूल बिंदु के संदर्भ में निर्धारित करने के लिए किया जाता है।
इस लेख में, आइए स्थिति सदिशों, उनकी परिभाषा, हल किए गए उदाहरणों के साथ सूत्रों के बारे में जानें।
स्थिति सदिश एक सरल रेखा है जिसका एक छोर किसी पिंड से जुड़ा होता है और दूसरा छोर किसी गतिशील बिंदु से जुड़ा होता है और इसका उपयोग पिंड के सापेक्ष बिंदु की स्थिति का वर्णन करने के लिए किया जाता है। जैसे-जैसे बिंदु गति करता है, स्थिति सदिश लंबाई या दिशा में या लंबाई और दिशा दोनों में बदलेगा।
परिभाषा
स्थिति सदिश, को एक सदिश के रूप में परिभाषित किया जाता है जो किसी भी मनमाने संदर्भ बिंदु जैसे मूल के संबंध में किसी भी दिए गए बिंदु की स्थिति या स्थान को इंगित करता है। स्थिति सदिश की दिशा सदैव उस सदिश के मूल से दिए गए बिंदु की ओर इंगित करती है।
- कार्टेशियन निर्देशांक प्रणाली में, यदि मूल बिंदु है और एक अन्य बिंदु है, तो बिंदु से बिंदु तक निर्देशित होने वाला स्थिति सदिश के रूप में दर्शाया जा सकता है।
- त्रि-आयामी अंतरिक्ष में, यदि मूल बिंदु और है, तो बिंदु का स्थिति सदिश v इस प्रकार दर्शाया जा सकता है:
आइए दो सदिशों, और पर विचार करें, जिनके स्थान सदिश क्रमशः और हैं। सदिश और के निर्देशांक इस प्रकार लिखे जा सकते हैं: । आइए नीचे दी गई छवि में दिखाए गए मूल बिंदु O पर विचार करें। हम एक कण पर विचार करेंगे जो बिंदु से बिंदु तक गति करता है। किसी कण के स्थान सदिश को उस सदिश के रूप में परिभाषित किया जा सकता है जो मूल बिंदु से उस बिंदु तक प्रारंभ होता है जहाँ कण स्थित है।
उपरोक्त चित्र में, जब कण बिंदु पर होता है तो उसका स्थिति सदिश होता है और जब वह बिंदु पर होता है तो होता है।
स्थिति सदिश कैसे ज्ञात करें?
किसी बिंदु का स्थिति सदिश ज्ञात करने से पहले, उसके निर्देशांक निर्धारित करना आवश्यक है। दो बिंदुओं, और पर विचार करें, जहाँ और है।
इसके बाद, हम बिंदु से बिंदु तक स्थिति सदिश, सदिश AB ज्ञात करेंगे।
इस स्थिति सदिश को निर्धारित करने के लिए, हमें के संगत घटकों को से घटाना होगा:
स्थिति सदिश सूत्र
यदि हम -तल में किसी बिंदु की स्थिति जानते हैं, तो हम उन दो बिंदुओं के बीच स्थिति सदिश निर्धारित करने के लिए सूत्र का उपयोग कर सकते हैं। उदाहरण के लिए, एक बिंदु पर विचार करें, जिसके निर्देशांक -तल में हैं, और दूसरा बिंदु , जिसके निर्देशांक हैं।
- से तक स्थिति सदिश निर्धारित करने का सूत्र है।
- स्थिति सदिश एक सदिश को संदर्भित करता है जो बिंदु से प्रारंभ होता है और बिंदु पर समाप्त होता है।
- इसी तरह, यदि हम बिंदु से बिंदु तक स्थिति सदिश ज्ञात करना चाहते हैं, तो हम इसका उपयोग कर सकते हैं:
उदाहरण
उदाहरण: दो बिंदु और दिए होने पर स्थिति सदिश निर्धारित करें।
समाधान: यदि -निर्देशांक प्रणाली में दो बिंदु दिए गए हैं, तो हम स्थिति सदिश ज्ञात करने के लिए निम्नलिखित सूत्र का उपयोग कर सकते हैं:
जहाँ बिंदु के निर्देशांकों को दर्शाता है और बिंदु के निर्देशांकों को दर्शाता है। ध्यान दें कि स्थिति सदिश बिंदु से बिंदु की ओर निर्देशित एक सदिश को दर्शाता है। यह स्थिति सदिश से भिन्न है, जो से की ओर निर्देशित होता है। इस प्रकार, उपरोक्त समीकरण में केवल बिंदु और के मान डालकर, हम स्थिति सदिश ज्ञात कर सकते हैं:
इस प्रकार, स्थिति सदिश मूल बिंदु से प्रारंभ होने वाले सदिश के बराबर है। यह सदिश 9 इकाइयों के बिंदु पर निर्देशित होता है जो -अक्ष के साथ बाईं ओर और -अक्ष के साथ 5 इकाइयों नीचे की ओर होता है।
महत्वपूर्ण टिप्पणियाँ
यहाँ कुछ बिंदुओं की सूची दी गई है जिन्हें स्थिति सदिश का अध्ययन करते समय याद रखना चाहिए
- स्थिति सदिश को एक सदिश के रूप में परिभाषित किया जाता है जो मूल बिंदु जैसे किसी भी मनमाने संदर्भ बिंदु के संबंध में किसी दिए गए बिंदु की स्थिति या स्थान को इंगित करता है।
- स्थिति सदिश की दिशा सदैव उस सदिश के मूल बिंदु से दिए गए बिंदु की ओर इंगित करती है।