समतल से दीए गए बिन्दु की दूरी: Difference between revisions

Latest revision as of 12:14, 17 December 2024

बिन्दु और समतल के बीच की दूरी दिए गए बिन्दु से गुजरने वाले समतल पर लंबवत की लंबाई है। दूसरे शब्दों में, हम कह सकते हैं कि बिन्दु और समतल के बीच की दूरी दिए गए बिन्दु से दिए गए समतल पर गिराए गए सामान्य सदिश की लंबाई है। यदि हम निर्देशांक $(x_{o},y_{o},z_{o})$ वाले बिन्दु $P$ और समीकरण $Ax+By+Cz=D$ के साथ दिए गए समतल के बीच की दूरी निर्धारित करना चाहते हैं, तो बिन्दु $P$ और दिए गए समतल के बीच की दूरी $\left\vert Ax_{o}+By_{o}+Cz_{o}+D\right\vert /{\sqrt {(A^{2}+B^{2}+C^{2})}}$ द्वारा दी जाती है।

परिभाषा

बिन्दु और समतल के बीच की दूरी, बिन्दु से दिए गए समतल तक की सबसे छोटी लंबवत दूरी है। सरल शब्दों में, किसी बिन्दु से समतल तक की सबसे छोटी दूरी दिए गए बिन्दु से दिए गए समतल पर गिराए गए सामान्य सदिश के समानांतर लंबवत की लंबाई है। आइए अब बिन्दु और समतल के बीच की दूरी का सूत्र देखेंगें ।

बिन्दु और समतल के बीच की दूरी का सूत्र

बिन्दु और समतल के बीच की सबसे छोटी दूरी सामान्य सदिश की लंबाई के बराबर होती है जो दिए गए बिन्दु से प्रारंभ होकर समतल को छूती है। निर्देशांक $(x_{o},y_{o},z_{o})$ वाले बिन्दु $P$ और समीकरण $Ax+By+Cz=D$ वाले दिए गए समतल $\pi$ पर विचार करें। फिर, बिन्दु $P$ और समतल $\pi$ के बीच की दूरी इस प्रकार दी गई है, $\left\vert Ax_{o}+By_{o}+Cz_{o}+D\right\vert /{\sqrt {(A^{2}+B^{2}+C^{2})}}$ ।

समतल से दीए गए बिन्दु की दूरी

बिन्दु और समतल के बीच की दूरी का प्रमाण

अब जब हम बिन्दु और समतल के बीच की दूरी का सूत्र जानते हैं, तो आइए हम त्रि-आयामी ज्यामिति के विभिन्न सूत्रों का उपयोग करके इसका सूत्र निकालें। त्रि-आयामी अंतरिक्ष में निर्देशांक $(x_{o},y_{o},z_{o})$ के साथ एक बिन्दु $P$ पर विचार करें, और सामान्य सदिश के साथ एक समतल, मान लें $v=(A,B,C)$ और समतल पर निर्देशांक $(x_{1},y_{1},z_{1})$ के साथ बिन्दु $Q$ । फिर समतल का समीकरण $A(x-x_{1})+B(y-y_{1})+C(z-z_{1})=0$ द्वारा दिया जाता है। इस समीकरण को $Ax+By+Cz+(-Ax_{1}-By_{1}-Cz_{1})=0\Rightarrow Ax+By+Cz+D=0$ के रूप में फिर से लिखा जा सकता है, जहाँ $D=-(Ax_{1}+By_{1}+Cz_{1})$ है। इसलिए, हमारे पास है:

समतल का समीकरण: $Ax+By+Cz+D=0$

बिन्दु $P:(x_{o},y_{o},z_{o})$

सामान्य सदिश: $Ai+Bj+Ck$

मान लीजिए कि $w$ , बिन्दु $P(x_{o},y_{o},z_{o})$ और $Q(x_{1},y_{1},z_{1})$ को जोड़ने वाला सदिश है। फिर, $w=(x_{o}-x_{1},y_{o}-y_{1},z_{o}-z_{1})$ । अब, इकाई सामान्य सदिश की गणना करें, यानी, 1 के बराबर परिमाण वाला सामान्य सदिश जो सामान्य सदिश $v$ को उसके परिमाण से भाग देकर प्राप्त किया जाता है। इकाई सामान्य सदिश इस प्रकार दिया जाता है,

$n=v/||v||$

$=(A,B,C)/{\sqrt {(A^{2}+B^{2}+C^{2})}}$

अब, बिन्दु $P$ और दिए गए समतल के बीच की दूरी इकाई सामान्य सदिश $n$ पर सदिश $w$ के प्रक्षेपण की लंबाई के अतिरिक्त और कुछ नहीं है। जैसा कि हम जानते हैं, सदिश $n$ की लंबाई एक के बराबर है, बिन्दु $P$ से समतल तक की दूरी सदिश $w$ और $n$ के डॉट गुणनफल का निरपेक्ष मान है, अर्थात,

दूरी, $d=|w\cdot n|$

$=|(x_{o}-x_{1},y_{o}-y_{1},z_{o}-z_{1})\cdot [(A,B,C)/{\sqrt {(A^{2}+B^{2}+C^{2})}}]|$

$=|A(x_{o}-x_{1})+B(y_{o}-y_{1})+C(z_{o}-z_{1})|/{\sqrt {(A^{2}+B^{2}+C^{2})}}$

$=|Ax_{o}+By_{o}+Cz_{o}-(Ax_{1}+By_{1}+Cz_{1})|/{\sqrt {(A^{2}+B^{2}+C^{2})}}$

$=|Ax_{o}+By_{o}+Cz_{o}+D|/{\sqrt {(A^{2}+B^{2}+C^{2})}}$ [क्योंकि $D=-(Ax_{1}+By_{1}+Cz_{1})$ ]

चूँकि निर्देशांक $(x_{1},y_{1},z_{1})$ वाला बिन्दु $Q$ दिए गए समतल पर एक मनमाना बिन्दु है और $D=-(Ax_{1}+By_{1}+Cz_{1})$ है, इसलिए समतल पर किसी भी बिन्दु $Q$ के लिए सूत्र समान रहता है और इसलिए, बिन्दु $Q$ पर निर्भर नहीं करता है, यानी, बिन्दु $Q$ समतल पर जहाँ भी स्थित हो, बिन्दु और समतल के बीच की दूरी का सूत्र समान रहता है। इसलिए, बिन्दु $P(x_{o},y_{o},z_{o})$ और समतल $\pi :Ax+By+Cz+D=0$ के बीच की दूरी इस प्रकार दी गई है, $d=|Ax_{o}+By_{o}+Cz_{o}+D|/{\sqrt {(A^{2}+B^{2}+C^{2})}}$

बिन्दु से समतल तक की दूरी का सूत्र लागू करने की विधि

हमने एक बिन्दु से समतल तक की दूरी का सूत्र निकाला है, हम इसके अनुप्रयोग को समझने और बिन्दु और समतल के बीच की दूरी निर्धारित करने के लिए सूत्र का उपयोग करके एक उदाहरण हल करेंगे।

उदाहरण

उदाहरण: बिन्दु $P=(1,2,5)$ और समतल $\pi :3x+4y+z+7=0$ के बीच की दूरी निर्धारित करें

हल: हम जानते हैं कि बिन्दु और समतल के बीच की दूरी का सूत्र है: $d=|Ax_{o}+By_{o}+Cz_{o}+D|/{\sqrt {(A^{2}+B^{2}+C^{2})}}$

यहाँ $,A=3,B=4,C=1,D=7,x_{o}=1,y_{o}=2,z_{o}=5$

सूत्र में मान प्रतिस्थापित करने पर, हमें यह प्राप्त होता है

$d=|Ax_{o}+By_{o}+Cz_{o}+D|/{\sqrt {(A^{2}+B^{2}+C^{2})}}$

$=|3\times 1+4\times 2+1\times 5+7|/{\sqrt {(3^{2}+4^{2}+1^{2})}}$

$=|3+8+5|/{\sqrt {(9+16+1)}}$

$=|16|/{\sqrt {26}}$

$=8{\sqrt {26/13}}$ इकाइयाँ

महत्वपूर्ण टिप्पणियाँ

बिन्दु और समतल के बीच की दूरी का सूत्र: $|Ax_{o}+By_{o}+Cz_{o}+D|/{\sqrt {(A^{2}+B^{2}+C^{2})}}$
यदि दिया गया बिन्दु दिए गए समतल पर स्थित है, तो बिन्दु और समतल के बीच की दूरी शून्य है।

@@ Line 1: / Line 1: @@
-बिंदु और समतल के बीच की दूरी दिए गए बिंदु से गुजरने वाले समतल पर लंबवत की लंबाई है। दूसरे शब्दों में, हम कह सकते हैं कि बिंदु और समतल के बीच की दूरी दिए गए बिंदु से दिए गए समतल पर गिराए गए सामान्य वेक्टर की लंबाई है। यदि हम निर्देशांक (xo, yo, zo) वाले बिंदु P और समीकरण Ax + By + Cz = D के साथ दिए गए समतल के बीच की दूरी निर्धारित करना चाहते हैं, तो बिंदु P और दिए गए समतल के बीच की दूरी |Axo + Byo+ Czo + D|/√(A2 + B2 + C2) द्वारा दी जाती है।
+बिन्दु और समतल के बीच की दूरी दिए गए बिन्दु  से गुजरने वाले समतल पर लंबवत की लंबाई है। दूसरे शब्दों में, हम कह सकते हैं कि बिन्दु  और समतल के बीच की दूरी दिए गए बिन्दु  से दिए गए समतल पर गिराए गए सामान्य सदिश   की लंबाई है। यदि हम निर्देशांक <math>(x_o, y_o, z_o)</math> वाले बिन्दु  <math>P</math> और समीकरण  <math>Ax + By + Cz = D</math> के साथ दिए गए समतल के बीच की दूरी निर्धारित करना चाहते हैं, तो बिन्दु  <math>P</math> और दिए गए समतल के बीच की दूरी   <math>\left\vert Ax_o + By_o+ Cz_o + D \right\vert/ \sqrt{(A^2 + B^2 + C^2)}</math> द्वारा दी जाती है।
 == परिभाषा ==
-बिंदु और समतल के बीच की दूरी बिंदु से दिए गए समतल तक की सबसे छोटी लंबवत दूरी है। सरल शब्दों में, किसी बिंदु से समतल तक की सबसे छोटी दूरी दिए गए बिंदु से दिए गए समतल पर गिराए गए सामान्य वेक्टर के समानांतर लंबवत की लंबाई है। आइए अब बिंदु और समतल के बीच की दूरी का सूत्र देखें।
+बिन्दु और समतल के बीच की दूरी, बिन्दु  से दिए गए समतल तक की सबसे छोटी लंबवत दूरी है। सरल शब्दों में, किसी बिन्दु  से समतल तक की सबसे छोटी दूरी दिए गए बिन्दु  से दिए गए समतल पर गिराए गए सामान्य [[सदिश योग का समांतर चतुर्भुज नियम|सदिश]]  के समानांतर लंबवत की लंबाई है। आइए अब बिन्दु और समतल के बीच की दूरी का सूत्र देखेंगें ।
-== बिंदु और समतल के बीच की दूरी का सूत्र ==
+== बिन्दु और समतल के बीच की दूरी का सूत्र ==
-बिंदु और समतल के बीच की सबसे छोटी दूरी सामान्य वेक्टर की लंबाई के बराबर होती है जो दिए गए बिंदु से शुरू होकर समतल को छूती है। निर्देशांक (xo, yo, zo) वाले बिंदु P और समीकरण Ax + By + Cz = D वाले दिए गए समतल π पर विचार करें। फिर, बिंदु P और समतल π के बीच की दूरी इस प्रकार दी गई है, |Axo + Byo+ Czo + D|/√(A2 + B2 + C2)।
+बिन्दु  और समतल के बीच की सबसे छोटी दूरी सामान्य सदिश   की लंबाई के बराबर होती है जो दिए गए बिन्दु  से प्रारंभ होकर समतल को छूती है। निर्देशांक <math>(x_o, y_o, z_o)</math> वाले बिन्दु  <math>P</math> और समीकरण <math>Ax + By + Cz = D</math> वाले दिए गए समतल <math>\pi</math> पर विचार करें। फिर, बिन्दु  <math>P</math> और समतल <math>\pi</math> के बीच की दूरी इस प्रकार दी गई है, <math>\left\vert Ax_o + By_o+ Cz_o + D \right\vert/ \sqrt{(A^2 + B^2 + C^2)}</math>।
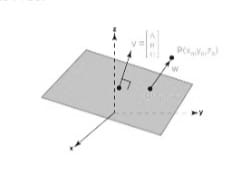
+[[File:समतल से दीए गए बिन्दु की दूरी.jpg|thumb|समतल से दीए गए बिन्दु की दूरी]]
-== बिंदु और समतल के बीच की दूरी का प्रमाण ==
+== बिन्दु और समतल के बीच की दूरी का प्रमाण ==
-अब जब हम बिंदु और समतल के बीच की दूरी का सूत्र जानते हैं, तो आइए हम त्रि-आयामी ज्यामिति के विभिन्न सूत्रों का उपयोग करके इसका सूत्र निकालें। त्रि-आयामी अंतरिक्ष में निर्देशांक (xo, yo, zo) के साथ एक बिंदु P पर विचार करें, और सामान्य वेक्टर के साथ एक समतल, मान लें v = (A, B, C) और समतल पर निर्देशांक (x1, y1, z1) के साथ बिंदु Q। फिर समतल का समीकरण A(x - x1) + B(y - y1) + C(z - z1) = 0 द्वारा दिया जाता है। इस समीकरण को Ax + By + Cz + (- Ax1 - By1 - Cz1) = 0 ⇒ Ax + By + Cz + D = 0 के रूप में फिर से लिखा जा सकता है, जहाँ D = - (Ax1 + By1 + Cz1) है। इसलिए, हमारे पास है:
+अब जब हम बिन्दु  और समतल के बीच की दूरी का सूत्र जानते हैं, तो आइए हम त्रि-आयामी ज्यामिति के विभिन्न सूत्रों का उपयोग करके इसका सूत्र निकालें। त्रि-आयामी [[अंतरिक्ष में एक बिन्दु के निर्देशांक|अंतरिक्ष]] में निर्देशांक <math>(x_o, y_o, z_o)</math> के साथ एक बिन्दु  <math>P</math> पर विचार करें, और सामान्य सदिश   के साथ एक समतल, मान लें <math>v = (A, B, C)</math> और समतल पर निर्देशांक <math>(x_1, y_1, z_1)</math> के साथ बिन्दु <math>Q</math>। फिर समतल का समीकरण <math>A(x - x_1) + B(y - y_1) + C(z - z_1) = 0</math> द्वारा दिया जाता है। इस समीकरण को <math>Ax + By + Cz + (- Ax_1 - By_1 - Cz_1) = 0 \Rightarrow Ax + By + Cz + D = 0</math> के रूप में फिर से लिखा जा सकता है, जहाँ <math>D = - (Ax_1 + By_1 + Cz_1)</math> है। इसलिए, हमारे पास है:
-समतल का समीकरण: Ax + By + Cz + D = 0
+समतल का समीकरण:  <math>Ax + By + Cz +D=0</math>
-बिंदु P: (xo, yo, zo)
+बिन्दु  <math>P: (x_o, y_o, z_o)</math>
-सामान्य सदिश: Ai + Bj + Ck
+सामान्य सदिश: <math>Ai + Bj + Ck</math>
-मान लीजिए कि w, बिंदु P(xo, yo, zo) और Q(x1, y1, z1) को जोड़ने वाला सदिश है। फिर, w = (xo - x1, yo - y1, zo - z1)। अब, इकाई सामान्य सदिश की गणना करें, यानी, 1 के बराबर परिमाण वाला सामान्य सदिश जो सामान्य सदिश v को उसके परिमाण से भाग देकर प्राप्त किया जाता है। इकाई सामान्य सदिश इस प्रकार दिया जाता है,
+मान लीजिए कि <math>w</math>, बिन्दु <math>P(x_o, y_o, z_o)</math> और <math>Q(x_1, y_1, z_1)</math> को जोड़ने वाला सदिश है। फिर, <math>w = (x_o - x_1, y_o - y_1, z_o - z_1)</math>। अब, इकाई सामान्य सदिश की गणना करें, यानी, 1 के बराबर परिमाण वाला सामान्य सदिश जो सामान्य सदिश <math>v</math> को उसके परिमाण से भाग देकर प्राप्त किया जाता है। इकाई सामान्य सदिश इस प्रकार दिया जाता है,
-n = v/||v||
+<math>n = v/||v||</math>
-= (A, B, C)/√(A2 + B2 + C2)
+<math>= (A, B, C)/\sqrt{(A^2 + B^2 + C^2)}</math>
-अब, बिंदु P और दिए गए समतल के बीच की दूरी इकाई सामान्य सदिश n पर सदिश w के प्रक्षेपण की लंबाई के अलावा और कुछ नहीं है। जैसा कि हम जानते हैं, सदिश n की लंबाई एक के बराबर है, बिंदु P से समतल तक की दूरी सदिश w और n के डॉट उत्पाद का निरपेक्ष मान है, अर्थात,
+अब, बिन्दु  <math>P</math> और दिए गए समतल के बीच की दूरी इकाई सामान्य सदिश <math>n</math> पर सदिश <math>w</math> के प्रक्षेपण की लंबाई के अतिरिक्त और कुछ नहीं है। जैसा कि हम जानते हैं, सदिश <math>n</math> की लंबाई एक के बराबर है, बिन्दु  <math>P</math> से समतल तक की दूरी सदिश <math>w</math> और <math>n</math> के डॉट गुणनफल का निरपेक्ष मान है, अर्थात,
-दूरी, d = |w.n|
+दूरी, <math>d = |w\cdot n|</math>
-= | (xo - x1, yo - y1, zo - z1). [(A, B, C)/√(A<sup>2</sup> + B<sup>2</sup> + C<sup>2</sup>)] |
+<math>= | (x_o - x_1, y_o - y_1, z_o - z_1)\cdot [(A, B, C)/\sqrt{(A^2 + B^2 + C^2)}] |</math>
-= |A(xo - x1) + B(yo - y1) + C(zo - z1)|/√(A<sup>2</sup> + B<sup>2</sup> + C<sup>2</sup>)
+<math>= |A(x_o - x_1) + B(y_o - y_1) + C(z_o - z_1)|/\sqrt{(A^2 + B^2 + C^2)}</math>
-= | Axo + Byo + Czo - (Ax1 + By1 + Cz1) |/√(A<sup>2</sup> + B<sup>2</sup> + C<sup>2</sup>)
+<math>= | Ax_o + By_o + Cz_o - (Ax_1 + By_1 + Cz_1) |/\sqrt{(A^2 + B^2 + C^2)}</math>
-= | Axo + Byo + Czo + D |/√(A<sup>2</sup> + B<sup>2</sup> + C<sup>2</sup>) [Because D = - (Ax1 + By1 + Cz1)]
+<math>= | Ax_o + By_o + Cz_o + D |/\sqrt{(A^2 + B^2 + C^2)}</math> [क्योंकि <math>D = - (Ax_1 + By_1 + Cz_1)</math>]
-चूँकि निर्देशांक (x1, y1, z1) वाला बिंदु Q दिए गए समतल पर एक मनमाना बिंदु है और D = - (Ax1 + By1 + Cz1) है, इसलिए समतल पर किसी भी बिंदु Q के लिए सूत्र समान रहता है और इसलिए, बिंदु Q पर निर्भर नहीं करता है, यानी, बिंदु Q समतल पर जहाँ भी स्थित हो, बिंदु और समतल के बीच की दूरी का सूत्र समान रहता है। इसलिए, बिंदु P(xo, yo, zo) और समतल π: Ax + By + Cz + D = 0 के बीच की दूरी इस प्रकार दी गई है, d = |Axo + Byo + Czo + D |/√(A2 + B2 + C2)
+चूँकि निर्देशांक <math>(x_1, y_1, z_1)</math> वाला बिन्दु <math>Q</math> दिए गए समतल पर एक मनमाना बिन्दु  है और <math>D = - (Ax_1 + By_1 + Cz_1)</math> है, इसलिए समतल पर किसी भी बिन्दु  <math>Q</math> के लिए सूत्र समान रहता है और इसलिए, बिन्दु  <math>Q</math> पर निर्भर नहीं करता है, यानी, बिन्दु  <math>Q</math> समतल पर जहाँ भी स्थित हो, बिन्दु  और समतल के बीच की दूरी का सूत्र समान रहता है। इसलिए, बिन्दु  <math>P(x_o, y_o, z_o)</math> और समतल <math>\pi: Ax + By + Cz + D = 0</math> के बीच की दूरी इस प्रकार दी गई है, <math>d = |Ax_o + By_o + Cz_o + D |/\sqrt{(A^2 + B^2 + C^2)}</math>
-बिंदु से समतल तक की दूरी का सूत्र कैसे लागू करें?
+== बिन्दु से समतल तक की दूरी का सूत्र लागू करने की विधि ==
+हमने एक बिन्दु  से समतल तक की दूरी का सूत्र निकाला है, हम इसके अनुप्रयोग को समझने और बिन्दु  और समतल के बीच की दूरी निर्धारित करने के लिए सूत्र का उपयोग करके एक उदाहरण हल करेंगे।
-हमने एक बिंदु से समतल तक की दूरी का सूत्र निकाला है, हम इसके अनुप्रयोग को समझने और बिंदु और समतल के बीच की दूरी निर्धारित करने के लिए सूत्र का उपयोग करके एक उदाहरण हल करेंगे।
+== उदाहरण ==
+'''उदाहरण:''' बिन्दु  <math>P = (1, 2, 5)</math> और समतल <math>\pi: 3x + 4y + z + 7 = 0</math> के बीच की दूरी निर्धारित करें
-== Example ==
+हल: हम जानते हैं कि बिन्दु  और समतल के बीच की दूरी का सूत्र है: <math>d = |Ax_o + By_o + Cz_o + D |/\sqrt{(A^2 + B^2 + C^2)}</math>
-'''Example:''' Determine the distance between the point P = (1, 2, 5) and the plane π: 3x + 4y + z + 7 = 0
-'''Solution:''' We know that the formula for distance between point and plane is: d = |Axo + Byo + Czo + D |/√(A<sup>2</sup> + B<sup>2</sup> + C<sup>2</sup>)
+यहाँ <math>, A = 3, B = 4, C = 1, D = 7, x_o = 1, y_o = 2, z_o = 5</math>
-Here, A = 3, B = 4, C = 1, D = 7, xo = 1, yo = 2, zo = 5
+सूत्र में मान प्रतिस्थापित करने पर, हमें यह प्राप्त होता है
-Substituting the values in the formula, we have
+<math>d = |Ax_o + By_o + Cz_o + D |/\sqrt{(A^2 + B^2 + C^2)}</math>
-d = |Axo + Byo + Czo + D |/√(A<sup>2</sup> + B<sup>2</sup> + C<sup>2</sup>)
+<math>= |3 \times 1 + 4 \times  2 + 1 \times  5 + 7|/\sqrt{(3^2 + 4^2 + 1^2)}</math>
-= |3 × 1 + 4 × 2 + 1 × 5 + 7|/√(3<sup>2</sup> + 4<sup>2</sup> + 1<sup>2</sup>)
+<math>= |3 + 8 + 5|/\sqrt{(9 + 16 + 1)}</math>
-= |3 + 8 + 5|/√(9 + 16 + 1)
+<math>= |16|/\sqrt{26}</math>
-= |16|/√26
+<math>= 8\sqrt{26/13}</math>  इकाइयाँ
-= 8√26/13 units
+== महत्वपूर्ण टिप्पणियाँ ==
+* बिन्दु और समतल के बीच की दूरी का सूत्र: <math>|Ax_o + By_o + Cz_o + D |/\sqrt{(A^2 + B^2 + C^2)}</math>
-महत्वपूर्ण नोट्स
+* यदि दिया गया बिन्दु  दिए गए समतल पर स्थित है, तो बिन्दु  और समतल के बीच की दूरी शून्य है।
-* बिंदु और समतल के बीच की दूरी का सूत्र: |Axo + Byo + Czo + D |/√(A2 + B2 + C2)
-* यदि दिया गया बिंदु दिए गए समतल पर स्थित है, तो बिंदु और समतल के बीच की दूरी शून्य है।
 [[Category:त्रि-विमीय ज्यामिति]][[Category:गणित]][[Category:कक्षा-12]]