दो रेखाओं का सह-तलीय होना: Difference between revisions

Latest revision as of 15:36, 17 December 2024

ज्यामिति में दो शब्द हैं जो "co(सह)" से प्रारंभ होते हैं और एक जैसे और भ्रमित करने वाले लगते हैं। वे समरेखीय और सह-तलीय हैं। इनमें से प्रत्येक शब्द में, "co" का अर्थ है एक साथ, "रैखिक" का अर्थ है एक रेखा पर स्थित होना, और "प्लानर" का अर्थ है एक समतल पर स्थित होना। इस प्रकार, समरेखीय का अर्थ है कि एक साथ एक रेखा पर स्थित होना और सह-तलीय का अर्थ है कि एक साथ एक समतल पर स्थित होना।

आइए इस लेख में सह-तलीय बिंदुओं और सह-तलीय रेखाओं के बारे में अधिक जानें। साथ ही, आइए देखें कि निर्देशांक ज्यामिति में दिए गए बिंदुओं और दी गई रेखाओं के सह-तलीय होने का निर्धारण कैसे किया जाता है।

सह-तलीय का अर्थ

"सह-तलीय " शब्द का अर्थ है "एक ही तल पर स्थित होना"। तो स्पष्ट है, "गैर सह-तलीय " का अर्थ है "एक ही तल पर स्थित न होना"। ज्यामिति में, हम सह-तलीय ता के संबंध में दो चीजों का अध्ययन करते हैं:

सह-तलीय बिंदु
सह-तलीय रेखाएँ

सह-तलीय और गैर सह-तलीय बिंदु

जो बिंदु एक ही तल पर स्थित होते हैं उन्हें सह-तलीय बिंदु कहते हैं और इसलिए जो बिंदु एक ही तल पर नहीं होते हैं उन्हें गैर सह-तलीय बिंदु कहते हैं। हम जानते हैं कि $2D$ में दो बिंदु सदैव एक रेखा से होकर गुजर सकते हैं और इसलिए कोई भी दो बिंदु संरेखीय होते हैं। उसी तरह, $3D$ में तीन बिंदु सदैव एक तल से होकर गुजर सकते हैं और इसलिए कोई भी 3 बिंदु सदैव सह-तलीय होते हैं। लेकिन $3D$ में चार या उससे ज़्यादा बिंदु सह-तलीय नहीं हो सकते हैं।

सह-तलीय और गैर सह-तलीय रेखाएँ

दो या दो से अधिक रेखाएँ सह-तलीय कहलाती हैं यदि वे एक ही तल पर स्थित हों, और वे रेखाएँ जो एक ही तल पर स्थित न हों, उन्हें गैर-सह-तलीय रेखाएँ कहते हैं। निम्नलिखित आयताकार प्रिज्म पर विचार करें।

ज्यामिति में सह-तलीय रेखाएँ

ऊपर दिए गए आयताकार प्रिज्म में, यहाँ कुछ सह-तलीय रेखाएँ हैं:

$AD$ और $DH$ क्योंकि वे प्रिज्म के बाएँ पक्ष के चेहरे पर स्थित हैं (यानी, एक ही तल पर)।
$AB$ और $CD$ क्योंकि वे प्रिज्म के निचले चेहरे पर स्थित हैं (यानी, एक ही तल पर)।
$BC$ और $FG$ क्योंकि वे प्रिज्म के दाएँ पक्ष के चेहरे पर स्थित हैं (यानी, एक ही तल पर)।

निर्धारण

दो रेखाएँ सह-तलीय तब कहलाती हैं जब वे एक ही तल में उपस्थित हों। यहाँ दो रेखाओं के सदिश रूप और कार्टेशियन रूप दोनों में सह-तलीय होने की शर्तें दी गई हैं।

सदिश रूप में रेखाओं की सह-तलीयता के लिए शर्त

यदि दो रेखाओं के सदिश समीकरण ${\overrightarrow {r}}={\overrightarrow {a}}+k{\overrightarrow {p}}$ और ${\overrightarrow {r}}={\overrightarrow {b}}+k{\overrightarrow {q}}$ के रूप के हैं तो वे सहसमतलीय तभी होंगे यदि और केवल यदि $({\overrightarrow {b}}-{\overrightarrow {a}})\cdot ({\overrightarrow {p}}\times {\overrightarrow {q}})=0$

कार्टेशियन रूप में रेखाओं की सह-तलीयता के लिए शर्त

यदि दो रेखाओं के कार्टेशियन समीकरण ${\frac {x-x_{1}}{a_{1}}}={\frac {y-y_{1}}{b_{1}}}={\frac {z-z_{1}}{c_{1}}}$ और ${\frac {x-x_{2}}{a_{2}}}={\frac {y-y_{2}}{b_{2}}}={\frac {z-z_{2}}{c_{2}}}$ के रूप के हैं, तो रेखाएँ सहसमतलीय होती हैं यदि और केवल यदि निर्धारक सारणिक ${\begin{vmatrix}x_{2}-x_{1}&y_{2}-y_{1}&z_{2}-z_{1}\\a_{1}&b_{1}&c_{1}\\a_{2}&b_{2}&c_{2}\end{vmatrix}}=0$

महत्वपूर्ण टिप्पणियाँ

कोई भी दो बिंदु सदैव सह-तलीय होते हैं।
कोई भी तीन बिंदु सदैव सह-तलीय होते हैं।
चार या उससे अधिक बिंदु सह-तलीय होते हैं, यदि वे सभी एक ही तल पर उपस्थित हों।
दो या उससे अधिक रेखाएँ सह-तलीय होती हैं, यदि वे सभी एक ही तल पर उपस्थित हों।

@@ Line 1: / Line 1: @@
-Coplanarity of Two Lines
+ज्यामिति में दो शब्द हैं जो "co(सह)" से प्रारंभ होते हैं और एक जैसे और भ्रमित करने वाले लगते हैं। वे समरेखीय और सह-तलीय  हैं। इनमें से प्रत्येक शब्द में, "co" का अर्थ है एक साथ, "रैखिक" का अर्थ है एक रेखा पर स्थित होना, और "प्लानर" का अर्थ है एक समतल पर स्थित होना। इस प्रकार, समरेखीय का अर्थ है कि एक साथ एक रेखा पर स्थित होना और सह-तलीय  का अर्थ है कि एक साथ एक [[समतल से दीए गए बिन्दु की दूरी|समतल]] पर स्थित होना।
-[[Category:ज्यामिति]]
+आइए इस लेख में  सह-तलीय  बिंदुओं और सह-तलीय  रेखाओं के बारे में अधिक जानें। साथ ही, आइए देखें कि निर्देशांक ज्यामिति में दिए गए बिंदुओं और दी गई रेखाओं के सह-तलीय  होने का निर्धारण कैसे किया जाता है।
-[[Category:त्रि-विमीय ज्यामिति]][[Category:गणित]]
+== सह-तलीय का अर्थ ==
+"सह-तलीय " शब्द का अर्थ है "एक ही तल पर स्थित होना"। तो स्पष्ट है, "गैर सह-तलीय " का अर्थ है "एक ही तल पर स्थित न होना"। ज्यामिति में, हम सह-तलीय ता के संबंध में दो चीजों का अध्ययन करते हैं:
+* सह-तलीय  बिंदु
+* [[रेखा के समीकरणों के विविध रूप|सह-तलीय  रेखाएँ]]
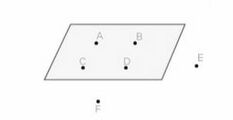
+[[File:सह-तलीय और गैर सह-तलीय बिंदु.jpg|thumb|233x233px|सह-तलीय और गैर सह-तलीय बिंदु]]
+=== सह-तलीय और गैर सह-तलीय  बिंदु ===
+जो बिंदु एक ही तल पर स्थित होते हैं उन्हें सह-तलीय  बिंदु कहते हैं और इसलिए जो बिंदु एक ही तल पर नहीं होते हैं उन्हें गैर सह-तलीय  बिंदु कहते हैं। हम जानते हैं कि <math>2D</math> में दो बिंदु सदैव एक रेखा से होकर गुजर सकते हैं और इसलिए कोई भी दो बिंदु संरेखीय होते हैं। उसी तरह, <math>3D</math> में तीन बिंदु सदैव एक तल से होकर गुजर सकते हैं और इसलिए कोई भी 3 बिंदु सदैव सह-तलीय  होते हैं। लेकिन <math>3D</math> में चार या उससे ज़्यादा बिंदु सह-तलीय  नहीं हो सकते हैं।
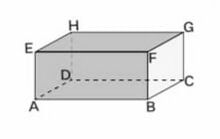
+[[File:सह-तलीय और गैर सह-तलीय रेखाएँ.jpg|thumb|220x220px|सह-तलीय और गैर सह-तलीय रेखाएँ]]
+=== सह-तलीय और गैर सह-तलीय रेखाएँ ===
+दो या दो से अधिक रेखाएँ सह-तलीय  कहलाती हैं यदि वे एक ही तल पर स्थित हों, और वे रेखाएँ जो एक ही तल पर स्थित न हों, उन्हें गैर-सह-तलीय  रेखाएँ कहते हैं। निम्नलिखित आयताकार प्रिज्म पर विचार करें।
+== ज्यामिति में सह-तलीय रेखाएँ ==
+ऊपर दिए गए आयताकार प्रिज्म में, यहाँ कुछ सह-तलीय रेखाएँ हैं:
+* <math>AD</math> और  <math>DH</math> क्योंकि वे प्रिज्म के बाएँ पक्ष के चेहरे पर स्थित हैं (यानी, एक ही तल पर)।
+* <math>AB</math> और  <math>CD</math> क्योंकि वे प्रिज्म के निचले चेहरे पर स्थित हैं (यानी, एक ही तल पर)।
+* <math>BC</math> और <math>FG</math>  क्योंकि वे प्रिज्म के दाएँ पक्ष के चेहरे पर स्थित हैं (यानी, एक ही तल पर)।
+== निर्धारण ==
+दो रेखाएँ सह-तलीय  तब कहलाती हैं जब वे एक ही तल में उपस्थित हों। यहाँ दो रेखाओं के सदिश रूप और कार्टेशियन रूप दोनों में सह-तलीय  होने की शर्तें दी गई हैं।
+=== सदिश रूप में रेखाओं की सह-तलीयता के लिए शर्त ===
+यदि दो रेखाओं के सदिश समीकरण <math>\overrightarrow{r} = \overrightarrow{a} + k \overrightarrow{p}</math> और <math>\overrightarrow{r} = \overrightarrow{b} + k \overrightarrow{q}</math> के रूप के हैं तो वे सहसमतलीय तभी होंगे यदि और केवल यदि <math>(\overrightarrow{b}- \overrightarrow{a})\cdot (\overrightarrow{p}\times \overrightarrow{q}) = 0</math>
+=== कार्टेशियन रूप में रेखाओं की सह-तलीयता के लिए शर्त ===
+यदि दो रेखाओं के कार्टेशियन समीकरण  <math>\frac{x-x_1}{a_1}=\frac{y-y_1}{b_1}=\frac{z-z_1}{c_1}</math> और  <math>\frac{x-x_2}{a_2}=\frac{y-y_2}{b_2}=\frac{z-z_2}{c_2}</math>  के रूप के हैं, तो रेखाएँ सहसमतलीय होती हैं यदि और केवल यदि निर्धारक सारणिक  <math>\begin{vmatrix} x_2-x_1  & y_2-y_1 & z_2-z_1 \\ a_1 &b_1&c_1 \\ a_2&b_2&c_2\end{vmatrix}=0</math>
+== महत्वपूर्ण टिप्पणियाँ ==
+* कोई भी दो बिंदु सदैव सह-तलीय  होते हैं।
+* कोई भी तीन बिंदु सदैव सह-तलीय  होते हैं।
+* चार या उससे अधिक बिंदु सह-तलीय  होते हैं, यदि वे सभी एक ही तल पर उपस्थित हों।
+* दो या उससे अधिक रेखाएँ सह-तलीय  होती हैं, यदि वे सभी एक ही तल पर उपस्थित हों।
+[[Category:त्रि-विमीय ज्यामिति]][[Category:गणित]][[Category:कक्षा-12]]