सदिश

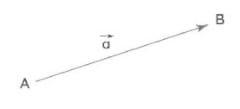
सदिश, ज्यामितीय इकाइयाँ हैं जिनमें परिमाण और दिशा होती है। सदिश को एक रेखा द्वारा दर्शाया जा सकता है जिसमें एक बाण चिन्ह उसकी दिशा की ओर संकेत करता है और इसकी लंबाई सदिश के परिमाण को दर्शाती है। इसलिए, सदिश को बाण चिन्ह द्वारा दर्शाया जाता है, उनके पास प्रारंभिक बिंदु और अन्त्य बिंदु होते हैं। सदिश की अवधारणा 200 वर्षों की अवधि में विकसित हुई थी। सदिश का उपयोग विस्थापन, वेग, त्वरण आदि जैसी भौतिक राशियों को दर्शाने के लिए किया जाता है।

इसके अतिरिक्त, सदिश का उपयोग 19वीं शताब्दी के अंत में विद्युत चुम्बकीय प्रेरण के क्षेत्र के आगमन के साथ प्रारंभ हुआ। यहाँ, हम सदिश की परिभाषा के साथ-साथ सदिश के गुणों, सदिश के सूत्रों, सदिश के संचालन के साथ-साथ बेहतर समझने का प्रयास करेंगे।

सदिश एक लैटिन शब्द है जिसका अर्थ है वाहक। सदिश एक बिंदु $A$ को बिंदु $B$ तक ले जाते हैं। दो बिंदुओं $A$ और $B$ के बीच की रेखा की लंबाई को सदिश का परिमाण कहा जाता है और बिंदु $A$ से बिंदु $B$ तक विस्थापन की दिशा को सदिश $AB$ की दिशा कहा जाता है। सदिश को यूक्लिडियन सदिश या स्थानिक सदिश भी कहा जाता है। सदिश के गणित, भौतिकी, इंजीनियरिंग और कई अन्य क्षेत्रों में कई अनुप्रयोग हैं।

यूक्लिडियन ज्यामिति में सदिश- परिभाषा

गणित में सदिश एक ज्यामितीय इकाई है जिसमें परिमाण और दिशा दोनों होते हैं। सदिशों में उस बिंदु पर एक प्रारंभिक बिंदु होता है जहाँ से वे प्रारंभ होते हैं और एक अन्त्य बिंदु होता है जो बिंदु की अंतिम स्थिति बताता है। सदिशों पर विभिन्न संक्रियाएँ लागू की जा सकती हैं जैसे जोड़, घटाव और गुणा। हम इस लेख में सदिशों पर संक्रियाओं का विस्तार से अध्ययन करेंगे।

सदिश - उदाहरण

भौतिकी में सदिश एक महत्वपूर्ण भूमिका निभाते हैं। उदाहरण के लिए, वेग, विस्थापन, त्वरण, बल सभी सदिश राशियाँ हैं जिनमें परिमाण के साथ-साथ दिशा भी होती है।

सदिश

सदिशों का निरूपण

सदिशों को साधारणतः बोल्ड लोअरकेस में दर्शाया जाता है जैसे कि $a$ या अक्षर के ऊपर बाण चिन्ह का उपयोग करके ${\overrightarrow {a}}$. सदिशों को उनके आरंभिक और अंतिम बिंदुओं द्वारा उनके ऊपर बाण चिन्ह से भी दर्शाया जा सकता है, उदाहरण के लिए, सदिश $AB$ को _{${\overrightarrow {AB}}$} के रूप में दर्शाया जा सकता है. सदिश के निरूपण का मानक रूप ${\overrightarrow {A}}=a{\overset {\frown }{i}}+b{\overset {\frown }{j}}+c{\overset {\frown }{k}}$है. यहाँ, $a,b,c$ वास्तविक संख्याएँ हैं और ${\overset {\frown }{i}},{\overset {\frown }{j}},{\overset {\frown }{k}}$ क्रमशः $x$-अक्ष, $y$-अक्ष और $z$-अक्ष के साथ इकाई सदिश हैं.

सदिश के आरंभिक बिंदु को पूंछ भी कहा जाता है जबकि अंतिम बिंदु को सिर कहा जाता है। सदिश किसी वस्तु की एक स्थान से दूसरे स्थान पर गति का वर्णन करते हैं। कार्टेशियन निर्देशांक प्रणाली में, सदिश को क्रमित युग्मों द्वारा दर्शाया जा सकता है। इसी तरह, '$n$' आयामों में सदिश को '$n$' टपल द्वारा दर्शाया जा सकता है। सदिश को घटकों के टपल से भी पहचाना जाता है जो आधार सदिश के एक समुच्चय के लिए अदिश गुणांक होते हैं। आधार सदिश को इस प्रकार दर्शाया जाता है: $e_{1}=(1,0,0),e_{2}=(0,1,0),e_{3}=(0,0,1)$

सदिश का सूत्र

किसी सदिश के परिमाण की गणना उसके घटकों के वर्गों के योग का वर्गमूल लेकर की जा सकती है। यदि $(x,y,z)$सदिश $A$ के घटक हैं, तो $A$ का परिमाण सूत्र इस प्रकार दिया जाता है,

$|A|={\sqrt {(x^{2}+y^{2}+z^{2})}}$

किसी भी प्रकार का अभिलेख का क्रम एक आदिश मन होता है।

• $(a_{1}{\overset {\frown }{i}}+b_{1}{\overset {\frown }{j}}+c_{1}{\overset {\frown }{k}})+(a_{2}{\overset {\frown }{i}}+b_{2}{\overset {\frown }{j}}+c_{2}{\overset {\frown }{k}})=(a_{1}+a_{2}){\overset {\frown }{i}}+(b_{1}+b_{2}){\overset {\frown }{j}}+(c_{1}+c_{2}){\overset {\frown }{k}}$
• $(a_{1}{\overset {\frown }{i}}+b_{1}{\overset {\frown }{j}}+c_{1}{\overset {\frown }{k}})-(a_{2}{\overset {\frown }{i}}+b_{2}{\overset {\frown }{j}}+c_{2}{\overset {\frown }{k}})=(a_{1}-a_{2}){\overset {\frown }{i}}+(b_{1}-b_{2}){\overset {\frown }{j}}+(c_{1}-c_{2}){\overset {\frown }{k}}$
• $(a_{1}{\overset {\frown }{i}}+b_{1}{\overset {\frown }{j}}+c_{1}{\overset {\frown }{k}})\cdot (a_{2}{\overset {\frown }{i}}+b_{2}{\overset {\frown }{j}}+c_{2}{\overset {\frown }{k}})=(a_{1}\cdot a_{2})+(b_{1}\cdot b_{2})+(c_{1}\cdot c_{2})$
• ${\overrightarrow {A}}\times {\overrightarrow {B}}={\overset {\frown }{i}}(a_{2}b_{3}-a_{3}b_{2})-{\overset {\frown }{j}}(a_{1}b_{3}-a_{3}b_{1})+{\overset {\frown }{k}}(a_{1}b_{2}-a_{2}b_{1})$
• $\theta =cos^{-1}(a\cdot b/|a||b|)$

सदिशों के गुणधर्म

सदिशों के निम्नलिखित गुण सदिशों को बेहतर ढंग से समझने में मदद करते हैं और सदिशों से संबंधित कई अंकगणितीय संक्रियाएँ करने में उपयोगी होते हैं।

• सदिशों का योग क्रमविनिमेय और साहचर्य होता है।
• ${\overrightarrow {A}}\cdot {\overrightarrow {B}}={\overrightarrow {B}}\cdot {\overrightarrow {A}}$
• ${\overrightarrow {A}}\times {\overrightarrow {B}}\neq {\overrightarrow {B}}\times {\overrightarrow {A}}$
• ${\overset {\frown }{i}}\cdot {\overset {\frown }{i}}={\overset {\frown }{j}}\cdot {\overset {\frown }{j}}={\overset {\frown }{k}}\cdot {\overset {\frown }{k}}=1$
• ${\overset {\frown }{i}}\cdot {\overset {\frown }{j}}={\overset {\frown }{j}}\cdot {\overset {\frown }{k}}={\overset {\frown }{k}}\cdot {\overset {\frown }{i}}=0$
• ${\overset {\frown }{i}}\times {\overset {\frown }{i}}={\overset {\frown }{j}}\times {\overset {\frown }{j}}={\overset {\frown }{k}}\times {\overset {\frown }{k}}=0$
• ${\overrightarrow {i}}\times {\overrightarrow {j}}={\overrightarrow {k}};{\overrightarrow {j}}\times {\overrightarrow {k}}={\overrightarrow {i}};{\overrightarrow {k}}\times {\overrightarrow {i}}={\overrightarrow {j}}$
• ${\overrightarrow {j}}\times {\overrightarrow {i}}={\overrightarrow {-k}};{\overrightarrow {k}}\times {\overrightarrow {j}}={\overrightarrow {-i}};{\overrightarrow {i}}\times {\overrightarrow {k}}={\overrightarrow {-j}}$
• दो सदिशों का डॉट गुणनफल एक अदिश राशि है और दो सदिशों के तल में स्थित होता है।
• दो सदिशों का वज्र गुणनफल एक सदिश है, जो इन दो सदिशों वाले तल के लंबवत होता है।

सदिशों के अनुप्रयोग

भौतिकी और गणित के क्षेत्र में सदिश बहुत उपयोगी होते हैं। इनका उपयोग वस्तुओं और भौतिक राशियों की स्थिति, विस्थापन, वेग और त्वरण को दर्शाने के लिए किया जाता है। सदिशों के कुछ अनुप्रयोग हैं,

• आंशिक अंतर समीकरणों और अंतर ज्यामिति के अध्ययन में सदिश बहुत महत्वपूर्ण भूमिका निभाते हैं।
• भौतिकी और इंजीनियरिंग में सदिशों का उपयोग किया जाता है, विशेष रूप से विद्युत चुम्बकीय क्षेत्र, गुरुत्वाकर्षण क्षेत्र और द्रव प्रवाह के उपयोग सहित क्षेत्रों में।

महत्वपूर्ण टिप्पणियाँ

सदिशों की अवधारणाओं को बेहतर ढंग से समझने के लिए निम्नलिखित महत्वपूर्ण टिप्पणियाँ सहायक हैं।

• ऑर्थोगोनल सदिशों का डॉट गुणनफल सदैव शून्य होता है।
• समानांतर सदिशों का वज्र गुणनफल सदैव शून्य होता है।
• दो या अधिक सदिश संरेखीय होते हैं यदि उनका वज्र गुणनफल शून्य हो।