रैखिक समीकरण युग्म का ग्राफीय विधि से हल: Difference between revisions
No edit summary |
(added internal links) |
||
| (9 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
जब गणितीय संक्रियाओं के साथ चरों और अचरों के गणितीय व्यंजक उच्चतम घात एक का [[समीकरण]] बनाते हैं, तो इसे एक रैखिक समीकरण कहा जाता है। रैखिक समीकरण चरों के बीच एक बीजीय समीकरण है जो आलेख पर अंकित करने पर एक सीधी रेखा देता है। एक चर का एक रैखिक समीकरण इस प्रकार का होता है <math>ax+b=0</math> जहां <math>x</math> चर है। दो चरों के [[रैखिक समीकरण]] इस रूप के होते हैं <math>ax+by+c=0</math> जहाँ <math>x</math> और <math>y</math> दो चर हैं और <math>c</math> स्थिरांक है। रैखिक समीकरणों की एक युग्म को दो मूल विधियों का उपयोग करके हल किया जा सकता है और दर्शाया जा सकता है: आलेखीय विधि और बीजगणितीय विधि। इस पाठ में, हम आलेखीय विधि का उपयोग करके दो रैखिक समीकरणों की एक प्रणाली को हल करने की विधि को ज्ञात करेंगे। | |||
[[Category: | == रैखिक समीकरण युग्म को आलेखीय रूप से हल करना == | ||
[[Category: | प्रत्येक रैखिक समीकरण में चर होते हैं। रैखिक समीकरण प्रथम कोटि के होते हैं और इनमें एक या दो चर उपस्थित हो सकते हैं। जब आलेखीय पद्धति का उपयोग करके रैखिक समीकरणों को हल करने की बात आती है तो मूल दृष्टिकोण उन्हें आलेख पर सीधी रेखाओं के रूप में प्रस्तुत करना और प्रतिच्छेदन बिंदु, यदि कोई हो, ज्ञात करना होता है। हम <math>x</math> के मानों को प्रतिस्थापित करके, <math>x</math> और <math>y</math> अंतःखंडों को ज्ञात करके और उन्हें आलेख पर ज्यामितीय रूप से आलेखन(प्लॉट) करके न्यूनतम दो समाधान सुलभ पद्धति से प्राप्त कर सकते हैं। आइए यहां रैखिक समीकरणों के एक युग्म के मानक रूप पर एक दृष्टि डालें। | ||
<math>a_1x+b_1y+c_1=0 ....(1)</math> | |||
<math>a_2x+b_2y+c_2=0 ....(2)</math> | |||
समीकरणों का हल रेखाओं की स्थिति के अनुसार भिन्न-भिन्न होता है। | |||
'''हल''' '''के प्रकार''' | |||
* '''संगत''': समीकरणों के युग्म को संगत कहा जाता है, यदि दो रेखाएँ एक ही बिंदु पर प्रतिच्छेद कर रही हों, तो वह बिंदु दोनों समीकरणों के लिए एक अद्वितीय हल देता है। | |||
* '''आश्रित''': समीकरणों के युग्म को आश्रित कहा जाता है, यदि दो रेखाएँ संपाती हों, तो इस स्थिति में अनंत रूप से कई हल होते हैं। एक रेखा पर प्रत्येक बिंदु एक हल बन जाता है। | |||
* '''असंगत''': समीकरणों के युग्म को असंगत कहा जाता है, यदि दो रेखाएँ समानांतर हों, तो इस स्थिति में कोई हल नहीं होता है। | |||
समीकरणों के निम्नलिखित तीन युग्मों पर विचार करें। | |||
(i) <math>x-2y=0</math> और <math>3x+4y-20=0</math> (रेखाएँ प्रतिच्छेद करती हैं ) | |||
(ii) <math>2x+3y-9=0</math> और <math>4x+6y-18=0</math> (रेखाएँ संपाती हैं ) | |||
(iii) <math>x+2y-4=0</math> और <math>2x+4y-12=0</math> (रेखाएँ समांतर हैं ) | |||
आइए उपर्युक्त तीनों उदाहरणों में <math>\frac{a_1}{a_2},\frac{b_1}{b_2},\frac{c_1}{c_2}</math> के मान लिखें और उनकी तुलना करें। | |||
यहाँ <math>a_1,b_1,c_1</math>और <math>a_2,b_2,c_2</math> सामान्य रूप <math>(1) </math> और <math>(2)</math> में दिए गए समीकरणों के गुणांकों को दर्शाता है | |||
{| class="wikitable" | |||
|+ | |||
!क्रमांक | |||
!रेखाओं का युग्म | |||
!<math>\frac{a_1}{a_2}</math> | |||
!<math>\frac{b_1}{b_2}</math> | |||
!<math>\frac{c_1}{c_2}</math> | |||
!अनुपातों की तुलना | |||
!आलेखीय विधि | |||
!बीजगणितीय व्याख्या | |||
|- | |||
|1 | |||
|<math>x+3y-6=0</math> | |||
<math>2x-3y-12=0</math> | |||
!<math>\frac{1}{2}</math> | |||
!<math>\frac{3}{-3}</math> | |||
!<math>\frac{-6}{-12}</math> | |||
!<math>\frac{a_1}{a_2} \ne \frac{b_1}{b_2}</math> | |||
|प्रतिच्छेदी रेखाएँ | |||
|सटीक रूप से एक हल (अद्वितीय) | |||
|- | |||
|2 | |||
| | |||
<math>2x+3y-9=0 </math> | |||
<math>4x+6y-18=0</math> | |||
!<math>\frac{2}{4}</math> | |||
!<math>\frac{3}{6}</math> | |||
!<math>\frac{-9}{-18}</math> | |||
!<math>\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}</math> | |||
|संयोग रेखाएँ | |||
|अनंत अनेक हल | |||
|- | |||
|3 | |||
|<math>x+2y-4=0</math> | |||
<math>2x+4y-12=0</math> | |||
!<math>\frac{1}{2}</math> | |||
!<math>\frac{2}{4}</math> | |||
!<math>\frac{-4}{-12}</math> | |||
!<math>\frac{a_1}{a_2}=\frac{b_1}{b_2}\ne \frac{c_1}{c_2}</math> | |||
|समानांतर रेखाएँ | |||
|कोई हल नहीं | |||
|} | |||
उपरोक्त तालिका से, यदि समीकरण द्वारा दर्शाई गई रेखाएँ | |||
<math>a_1x+b_1y+c_1=0 ....(1)</math> और <math>a_2x+b_2y+c_2=0 ....(2)</math> हैं | |||
* प्रतिच्छेद करते हुए, फिर <math>\frac{a_1}{a_2}\ne \frac{b_1}{b_2}</math> | |||
* संपाती, तो <math>\frac{a_1}{a_2}=\frac{b_1}{b_2}= \frac{c_1}{c_2}</math> | |||
* समांतर,फिर <math>\frac{a_1}{a_2}=\frac{b_1}{b_2}\ne \frac{c_1}{c_2}</math> | |||
== उदाहरण == | |||
1. आलेखीय रूप से जाँचें कि समीकरणों का युग्म सुसंगत है या नहीं । यदि हाँ, तो उन्हें आलेखीय रूप से हल करें। | |||
{| class="wikitable" | |||
|- | |||
|<math>x+3y-6=0</math> | |||
<math>2x-3y-12=0</math> | |||
|}'''हल :''' | |||
{| class="wikitable" | |||
|<math>x</math> | |||
|<math>0</math> | |||
|<math>6</math> | |||
|- | |||
|<math>y=\frac{6-x}{3}</math> | |||
|<math>2</math> | |||
|<math>0</math> | |||
|} | |||
{| class="wikitable" | |||
|+ | |||
|<math>x</math> | |||
|<math>0</math> | |||
|<math>3</math> | |||
|- | |||
|<math>y=\frac{2x-12}{3}</math> | |||
|<math>-4</math> | |||
|<math>-2</math> | |||
|} | |||
बिंदुओं को ग्राफ़ पेपर पर आलेखित करें | |||
* <math>(0,2)</math>, <math>(6,0)</math> और रेखाएँ बनाने के लिए बिंदुओं को मिलाएँ | |||
* <math>(0,-4)</math> <math>(3,-2)</math> और रेखाएँ बनाने के लिए बिंदुओं को मिलाएँ जैसा कि चित्र 1 में दिखाया गया है। | |||
[[File:Graph-1.jpg|alt=Fig.1|none|thumb|600x600px|चित्र .1]] | |||
हम देखते हैं कि दोनों रेखाओं में <math>(6,0)</math> पर एक बिंदु उभयनिष्ठ है। इसलिए, रैखिक समीकरणों के युग्म का हल <math>x=6</math>और <math>y=0</math> है, अर्थात, समीकरणों का दिया गया वायु संगत है। | |||
2. आलेखीय रूप से जाँच करें कि समीकरण युग्म के अनंत रूप से अनेक हल हैं या नहीं। यदि हाँ, तो उन्हें आलेखीय रूप से हल करें। | |||
{| class="wikitable" | |||
|- | |||
| | |||
<math>2x+3y-9=0 </math> | |||
<math>4x+6y-18=0</math> | |||
|}'''हल :''' | |||
{| class="wikitable" | |||
|<math>x</math> | |||
|<math>3</math> | |||
|<math>6</math> | |||
|- | |||
|<math>y=\frac{9-2x}{3}</math> | |||
|<math>1</math> | |||
|<math>-1</math> | |||
|} | |||
{| class="wikitable" | |||
|<math>x</math> | |||
|<math>3</math> | |||
|<math>6</math> | |||
|- | |||
|<math>y=\frac{18-4x}{6}</math> | |||
|<math>1</math> | |||
|<math>-1</math> | |||
|} | |||
बिंदुओं को ग्राफ़ पेपर पर आलेखित करें | |||
* <math>(3,1)</math>, <math>(6,-1)</math>और रेखाएँ बनाने के लिए बिंदुओं को मिलाएँ | |||
* <math>(3,1)</math> <math>(6,-1)</math>और रेखाएँ बनाने के लिए बिंदुओं को मिलाएँ जैसा कि चित्र 2 में दिखाया गया है। | |||
[[File:Graph-4.jpg|alt=Fig. 2|none|thumb|600x600px|चित्र .2]] | |||
हम देखते हैं कि रेखा पर स्थित प्रत्येक बिंदु एक हल बन जाता है। इसलिए, रैखिक समीकरणों के युग्म के हल के अनंत रूप से अनेक हल होते हैं। | |||
3. आलेखीय रूप से जाँच करें कि समीकरण युग्म के कोई हल है या नहीं है। यदि ऐसा है, तो उन्हें आलेखीय रूप से हल करें। | |||
{| class="wikitable" | |||
|- | |||
|<math>x+2y-4=0</math> | |||
<math>2x+4y-12=0</math> | |||
|} | |||
'''हल :''' | |||
{| class="wikitable" | |||
|<math>x</math> | |||
|<math>0</math> | |||
|<math>2</math> | |||
|- | |||
|<math>y=\frac{4-x}{2}</math> | |||
|<math>2</math> | |||
|<math>1</math> | |||
|} | |||
{| class="wikitable" | |||
|<math>x</math> | |||
|<math>0</math> | |||
|<math>2</math> | |||
|- | |||
|<math>y=\frac{12-2x}{4}</math> | |||
|<math>3</math> | |||
|<math>2</math> | |||
|} | |||
बिंदुओं को ग्राफ़ पेपर पर आलेखित करें | |||
* <math>(0,2)</math>, <math>(2,1)</math> और रेखाएँ बनाने के लिए बिंदुओं को मिलाएँ | |||
* <math>(0,3)</math> <math>(2,2)</math> और रेखाएँ बनाने के लिए बिंदुओं को मिलाएँ जैसा कि चित्र 3 में दिखाया गया है। | |||
[[File:Graph-parallel.jpg|alt=Fig. 3|none|thumb|600x600px|चित्र .3]] | |||
हम देखते हैं कि रेखाएँ एक दूसरे को प्रतिच्छेद नहीं कर रही हैं और एक दूसरे के समानांतर हैं। अतः, रैखिक समीकरण युग्म का कोई हल नहीं है। | |||
[[Category:दो चर वाले रैखिक समीकरण युग्म]] | |||
[[Category:गणित]] | |||
[[Category:कक्षा-10]] | |||
Latest revision as of 07:57, 11 October 2024
जब गणितीय संक्रियाओं के साथ चरों और अचरों के गणितीय व्यंजक उच्चतम घात एक का समीकरण बनाते हैं, तो इसे एक रैखिक समीकरण कहा जाता है। रैखिक समीकरण चरों के बीच एक बीजीय समीकरण है जो आलेख पर अंकित करने पर एक सीधी रेखा देता है। एक चर का एक रैखिक समीकरण इस प्रकार का होता है जहां चर है। दो चरों के रैखिक समीकरण इस रूप के होते हैं जहाँ और दो चर हैं और स्थिरांक है। रैखिक समीकरणों की एक युग्म को दो मूल विधियों का उपयोग करके हल किया जा सकता है और दर्शाया जा सकता है: आलेखीय विधि और बीजगणितीय विधि। इस पाठ में, हम आलेखीय विधि का उपयोग करके दो रैखिक समीकरणों की एक प्रणाली को हल करने की विधि को ज्ञात करेंगे।
रैखिक समीकरण युग्म को आलेखीय रूप से हल करना
प्रत्येक रैखिक समीकरण में चर होते हैं। रैखिक समीकरण प्रथम कोटि के होते हैं और इनमें एक या दो चर उपस्थित हो सकते हैं। जब आलेखीय पद्धति का उपयोग करके रैखिक समीकरणों को हल करने की बात आती है तो मूल दृष्टिकोण उन्हें आलेख पर सीधी रेखाओं के रूप में प्रस्तुत करना और प्रतिच्छेदन बिंदु, यदि कोई हो, ज्ञात करना होता है। हम के मानों को प्रतिस्थापित करके, और अंतःखंडों को ज्ञात करके और उन्हें आलेख पर ज्यामितीय रूप से आलेखन(प्लॉट) करके न्यूनतम दो समाधान सुलभ पद्धति से प्राप्त कर सकते हैं। आइए यहां रैखिक समीकरणों के एक युग्म के मानक रूप पर एक दृष्टि डालें।
समीकरणों का हल रेखाओं की स्थिति के अनुसार भिन्न-भिन्न होता है।
हल के प्रकार
- संगत: समीकरणों के युग्म को संगत कहा जाता है, यदि दो रेखाएँ एक ही बिंदु पर प्रतिच्छेद कर रही हों, तो वह बिंदु दोनों समीकरणों के लिए एक अद्वितीय हल देता है।
- आश्रित: समीकरणों के युग्म को आश्रित कहा जाता है, यदि दो रेखाएँ संपाती हों, तो इस स्थिति में अनंत रूप से कई हल होते हैं। एक रेखा पर प्रत्येक बिंदु एक हल बन जाता है।
- असंगत: समीकरणों के युग्म को असंगत कहा जाता है, यदि दो रेखाएँ समानांतर हों, तो इस स्थिति में कोई हल नहीं होता है।
समीकरणों के निम्नलिखित तीन युग्मों पर विचार करें।
(i) और (रेखाएँ प्रतिच्छेद करती हैं )
(ii) और (रेखाएँ संपाती हैं )
(iii) और (रेखाएँ समांतर हैं )
आइए उपर्युक्त तीनों उदाहरणों में के मान लिखें और उनकी तुलना करें।
यहाँ और सामान्य रूप और में दिए गए समीकरणों के गुणांकों को दर्शाता है
| क्रमांक | रेखाओं का युग्म | अनुपातों की तुलना | आलेखीय विधि | बीजगणितीय व्याख्या | |||
|---|---|---|---|---|---|---|---|
| 1 |
|
प्रतिच्छेदी रेखाएँ | सटीक रूप से एक हल (अद्वितीय) | ||||
| 2 |
|
संयोग रेखाएँ | अनंत अनेक हल | ||||
| 3 |
|
समानांतर रेखाएँ | कोई हल नहीं |
उपरोक्त तालिका से, यदि समीकरण द्वारा दर्शाई गई रेखाएँ
और हैं
- प्रतिच्छेद करते हुए, फिर
- संपाती, तो
- समांतर,फिर
उदाहरण
1. आलेखीय रूप से जाँचें कि समीकरणों का युग्म सुसंगत है या नहीं । यदि हाँ, तो उन्हें आलेखीय रूप से हल करें।
|
|
हल :
बिंदुओं को ग्राफ़ पेपर पर आलेखित करें
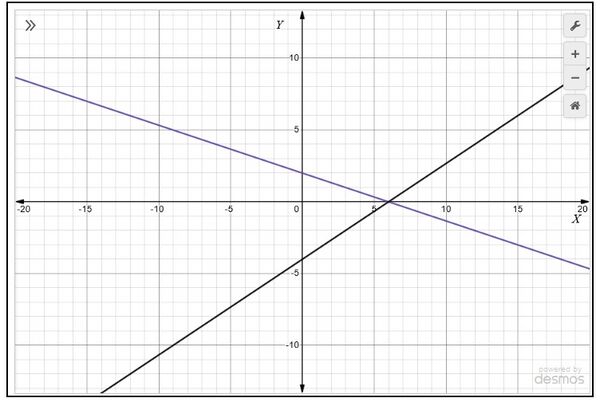
- , और रेखाएँ बनाने के लिए बिंदुओं को मिलाएँ
- और रेखाएँ बनाने के लिए बिंदुओं को मिलाएँ जैसा कि चित्र 1 में दिखाया गया है।
हम देखते हैं कि दोनों रेखाओं में पर एक बिंदु उभयनिष्ठ है। इसलिए, रैखिक समीकरणों के युग्म का हल और है, अर्थात, समीकरणों का दिया गया वायु संगत है।
2. आलेखीय रूप से जाँच करें कि समीकरण युग्म के अनंत रूप से अनेक हल हैं या नहीं। यदि हाँ, तो उन्हें आलेखीय रूप से हल करें।
|
|
हल :
बिंदुओं को ग्राफ़ पेपर पर आलेखित करें
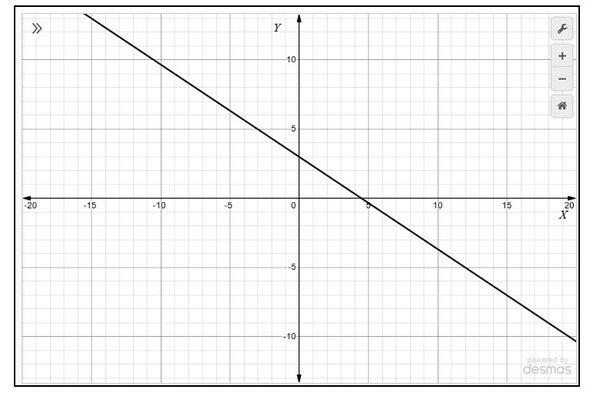
- , और रेखाएँ बनाने के लिए बिंदुओं को मिलाएँ
- और रेखाएँ बनाने के लिए बिंदुओं को मिलाएँ जैसा कि चित्र 2 में दिखाया गया है।
हम देखते हैं कि रेखा पर स्थित प्रत्येक बिंदु एक हल बन जाता है। इसलिए, रैखिक समीकरणों के युग्म के हल के अनंत रूप से अनेक हल होते हैं।
3. आलेखीय रूप से जाँच करें कि समीकरण युग्म के कोई हल है या नहीं है। यदि ऐसा है, तो उन्हें आलेखीय रूप से हल करें।
|
|
हल :
बिंदुओं को ग्राफ़ पेपर पर आलेखित करें
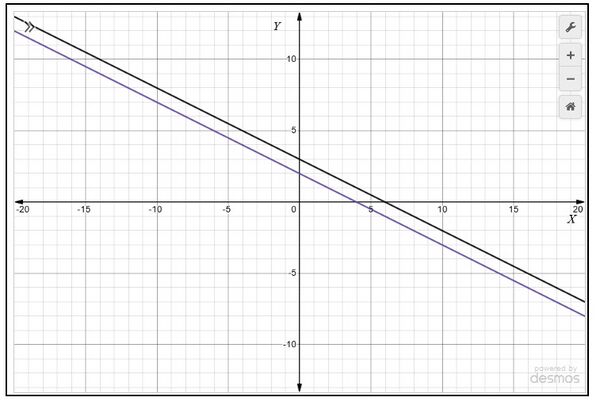
- , और रेखाएँ बनाने के लिए बिंदुओं को मिलाएँ
- और रेखाएँ बनाने के लिए बिंदुओं को मिलाएँ जैसा कि चित्र 3 में दिखाया गया है।
हम देखते हैं कि रेखाएँ एक दूसरे को प्रतिच्छेद नहीं कर रही हैं और एक दूसरे के समानांतर हैं। अतः, रैखिक समीकरण युग्म का कोई हल नहीं है।