त्रिकोणमितीय फलन: Difference between revisions
No edit summary |
(image added) |
||
| (9 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
त्रिकोणमितीय अनुपात को न्यून कोणों के लिए समकोण त्रिभुज की भुजाओं के अनुपात के रूप में परिभाषित किया गया है। रेडियन माप (वास्तविक संख्या) के संदर्भ में किसी भी कोण पर त्रिकोणमितीय अनुपात का विस्तार त्रिकोणमितीय फलन कहलाता है। | |||
[[Category: | [[त्रिकोणमितीय अनुपात|त्रिकोणमितीय]] फलन मूल छह फलन हैं जिनमें समकोण त्रिभुज के कोण के रूप में एक डोमेन इनपुट मान होता है, और सीमा के रूप में एक संख्यात्मक उत्तर होता है। <math>f(x) = sin\theta</math> के त्रिकोणमितीय फलन(जिसे 'ट्रिग फलन' भी कहा जाता है) का एक डोमेन होता है, जो डिग्री या रेडियन में दिया गया कोण <math>\theta</math> होता है, और इसकी सीमा <math>[-1, 1]</math> होती है। इसी तरह हमारे पास अन्य सभी फलन का डोमेन और सीमा है। त्रिकोणमितीय फलन कैलकुलस, [[ज्यामिति]] और बीजगणित में व्यापक रूप से उपयोग किए जाते हैं। | ||
नीचे दी गई सामग्री में, हम चार चतुर्भुजों में त्रिकोणमितीय फलन , उनके ग्राफ़, डोमेन और सीमा, सूत्र और त्रिकोणमितीय फलन के विभेदन, एकीकरण को समझने का लक्ष्य रखेंगे। हम इन छह त्रिकोणमितीय फलन और उनके अनुप्रयोगों की बेहतर समझ के लिए कुछ उदाहरणों को हल करेंगे। | |||
== त्रिकोणमितीय फलन क्या हैं? == | |||
त्रिकोणमिति में छह बुनियादी त्रिकोणमितीय फलन उपयोग किए जाते हैं। ये [[फलन]] त्रिकोणमितीय अनुपात हैं। छह बुनियादी त्रिकोणमितीय फलन साइन फलन, कोसाइन फलन, सेकेंट फलन, सह-सेकेंट फलन, स्पर्शज्या फलन और सह-स्पर्शज्या फलन हैं। त्रिकोणमितीय फलन और पहचान समकोण त्रिभुज की भुजाओं का अनुपात हैं। समकोण त्रिभुज की भुजाएँ लंबवत भुजा, कर्ण और आधार हैं, जिनका उपयोग त्रिकोणमितीय सूत्रों का उपयोग करके साइन, कोसाइन, स्पर्शज्या, सेकेंट, कोसेकेंट और कोटैंजेंट मानों की गणना करने के लिए किया जाता है। | |||
== त्रिकोणमितीय फलन सूत्र == | |||
हमारे पास समकोण त्रिभुज की भुजाओं का उपयोग करके त्रिकोणमितीय फलनों के मान ज्ञात करने के लिए कुछ सूत्र हैं। इन सूत्रों को लिखने के लिए, हम इन फलनों के संक्षिप्त रूप का उपयोग करते हैं। साइन को <math>sin</math>, कोसाइन को <math>cos</math>, स्पर्शज्या को <math>tan</math>, सेकेंट को <math>sec</math>, कोसेकेंट को <math>cosec</math> और कोटैंजेंट को <math>cot</math> लिखा जाता है। त्रिकोणमितीय फलनों को खोजने के लिए मूल सूत्र इस प्रकार हैं: | |||
<math>sin\theta=</math> लंब/कर्ण | |||
<math>cos\theta=</math> आधार/कर्ण | |||
<math>tan\theta=</math> लंब/आधार | |||
<math>sec\theta=</math> कर्ण/आधार | |||
<math>cosec\theta=</math> कर्ण/लंब | |||
<math>cot\theta=</math> आधार/लंब | |||
जैसा कि हम ऊपर दिए गए सूत्रों से देख सकते हैं, साइन और कोसेकेंट एक दूसरे के व्युत्क्रम हैं। इसी तरह, व्युत्क्रम युग्म कोसाइन और सेकेंट, तथा स्पर्शरेखा और कोटेंजेंट हैं। | |||
== त्रिकोणमितीय फलनों के मान == | |||
त्रिकोणमितीय फलनों का एक डोमेन <math>\theta</math> होता है, जो डिग्री या रेडियन में होता है। विभिन्न त्रिकोणमितीय फलनों के लिए <math>\theta</math> के कुछ मुख्य मान नीचे एक तालिका में प्रस्तुत किए गए हैं। इन मुख्य मानों को विशिष्ट कोणों पर त्रिकोणमितीय फलनों के मानक मान के रूप में भी संदर्भित किया जाता है और गणनाओं में प्रायः इनका उपयोग किया जाता है। त्रिकोणमितीय फलनों के मुख्य मान एक इकाई वृत्त से प्राप्त किए गए हैं। ये मान सभी त्रिकोणमितीय सूत्रों को भी संतुष्ट करते हैं। | |||
[[File:चार चतुर्थांशों में त्रिकोणमितीय फलन.jpg|thumb|चित्र-चार चतुर्थांशों में त्रिकोणमितीय फलन]] | |||
== चार चतुर्थांशों में त्रिकोणमितीय फलन == | |||
कोण <math>\theta</math> एक न्यून कोण <math>(\theta<90^\circ)</math> है और इसे धनात्मक <math>x</math>-अक्ष के संदर्भ में वामावर्त दिशा में मापा जाता है। इसके अलावा, इन त्रिकोणमितीय फलनों के अलग-अलग चतुर्थांशों में अलग-अलग संख्यात्मक चिह्न (<math>+</math> या <math>-</math>) होते हैं, जो चतुर्थांश के धनात्मक या ऋणात्मक अक्ष पर आधारित होते हैं। <math> sin\theta,cosec\theta</math> के त्रिकोणमितीय फलन चतुर्थांश I और II में धनात्मक हैं, और चतुर्थांश III और IV में ऋणात्मक हैं। सभी त्रिकोणमितीय फलनों की पहली चतुर्थांश में एक धनात्मक सीमा होती है। त्रिकोणमितीय फलन <math>tan\theta, cot\theta</math> केवल चतुर्थांश I और III में धनात्मक हैं, और <math>cos\theta,sec\theta,</math> के त्रिकोणमितीय अनुपात केवल चतुर्थांश I और IV में धनात्मक हैं। | |||
त्रिकोणमितीय कार्यों के प्रथम चतुर्थांश में <math>\theta</math>, <math>(90^\circ -\theta)</math> के मान होते हैं। सह-कार्य पहचान कोण <math>(90^\circ -\theta)</math> के लिए विभिन्न पूरक त्रिकोणमितीय कार्यों के बीच अंतर्संबंध प्रदान करती है। | |||
<math>sin(90^\circ -\theta)=cos\theta</math> | |||
<math>cos(90^\circ-\theta) =sin\theta</math> | |||
<math>tan(90^\circ-\theta)=cot\theta</math> | |||
<math>cot(90^\circ-\theta)=tan\theta</math> | |||
<math>sec(90^\circ-\theta) = cosec\theta</math> | |||
<math>cosec(90^\circ-\theta) = sec\theta</math> | |||
दूसरे चतुर्थांश में विभिन्न त्रिकोणमितीय कार्यों के लिए डोमेन <math>\theta</math> मान <math>\Bigl(\frac{\pi}{2}+\theta,\pi-\theta\Bigr)</math>है, तीसरे चतुर्थांश में <math>\Bigl(\pi+\theta,,\frac{3\pi}{2}-\theta\Bigr)</math>है, और चौथे चतुर्थांश में <math>\Bigl(\frac{3\pi}{2}+\theta,2\pi-\theta\Bigr)</math>है। <math>\frac{\pi}{2},\frac{3\pi}{2}</math>के लिए त्रिकोणमितीय मान उनके पूरक अनुपातों जैसे कि <math>sin\theta\Leftrightarrow cos\theta, </math> <math>tan\theta\Leftrightarrow cot\theta, </math> <math>sec\theta\Leftrightarrow cosec\theta </math> के रूप में बदलते हैं। <math>\pi,2\pi </math> के लिए त्रिकोणमितीय मान समान रहते हैं। विभिन्न चतुर्भुजों और कोणों में बदलते त्रिकोणमितीय अनुपातों को नीचे दी गई तालिका से समझा जा सकता है। | |||
[[File:त्रिकोणमितीय फलन ग्राफ.jpg|thumb|चित्र- त्रिकोणमितीय फलन ग्राफचित्र]] | |||
== त्रिकोणमितीय फलन ग्राफ == | |||
त्रिकोणमितीय फलनों के ग्राफ में <math>\theta</math> का डोमेन मान क्षैतिज <math>x</math>-अक्ष पर दर्शाया जाता है और सीमा मान ऊर्ध्वाधर <math>y</math>-अक्ष के साथ दर्शाया जाता है। <math>sin\theta </math> और <math>tan\theta </math> के ग्राफ मूल बिंदु से होकर गुजरते हैं और अन्य त्रिकोणमितीय फलनों के ग्राफ मूल बिंदु से होकर नहीं गुजरते हैं। <math>sin\theta </math> और <math>cos\theta </math> की सीमा<math>[-1, 1]</math> तक सीमित है। अनंत मानों की सीमा बिंदीदार रेखाओं के बगल में खींची गई है। | |||
[[Category:त्रिकोणमितीय फलन]][[Category:कक्षा-11]][[Category:गणित]] | |||
Latest revision as of 13:31, 13 November 2024
त्रिकोणमितीय अनुपात को न्यून कोणों के लिए समकोण त्रिभुज की भुजाओं के अनुपात के रूप में परिभाषित किया गया है। रेडियन माप (वास्तविक संख्या) के संदर्भ में किसी भी कोण पर त्रिकोणमितीय अनुपात का विस्तार त्रिकोणमितीय फलन कहलाता है।
त्रिकोणमितीय फलन मूल छह फलन हैं जिनमें समकोण त्रिभुज के कोण के रूप में एक डोमेन इनपुट मान होता है, और सीमा के रूप में एक संख्यात्मक उत्तर होता है। के त्रिकोणमितीय फलन(जिसे 'ट्रिग फलन' भी कहा जाता है) का एक डोमेन होता है, जो डिग्री या रेडियन में दिया गया कोण होता है, और इसकी सीमा होती है। इसी तरह हमारे पास अन्य सभी फलन का डोमेन और सीमा है। त्रिकोणमितीय फलन कैलकुलस, ज्यामिति और बीजगणित में व्यापक रूप से उपयोग किए जाते हैं।
नीचे दी गई सामग्री में, हम चार चतुर्भुजों में त्रिकोणमितीय फलन , उनके ग्राफ़, डोमेन और सीमा, सूत्र और त्रिकोणमितीय फलन के विभेदन, एकीकरण को समझने का लक्ष्य रखेंगे। हम इन छह त्रिकोणमितीय फलन और उनके अनुप्रयोगों की बेहतर समझ के लिए कुछ उदाहरणों को हल करेंगे।
त्रिकोणमितीय फलन क्या हैं?
त्रिकोणमिति में छह बुनियादी त्रिकोणमितीय फलन उपयोग किए जाते हैं। ये फलन त्रिकोणमितीय अनुपात हैं। छह बुनियादी त्रिकोणमितीय फलन साइन फलन, कोसाइन फलन, सेकेंट फलन, सह-सेकेंट फलन, स्पर्शज्या फलन और सह-स्पर्शज्या फलन हैं। त्रिकोणमितीय फलन और पहचान समकोण त्रिभुज की भुजाओं का अनुपात हैं। समकोण त्रिभुज की भुजाएँ लंबवत भुजा, कर्ण और आधार हैं, जिनका उपयोग त्रिकोणमितीय सूत्रों का उपयोग करके साइन, कोसाइन, स्पर्शज्या, सेकेंट, कोसेकेंट और कोटैंजेंट मानों की गणना करने के लिए किया जाता है।
त्रिकोणमितीय फलन सूत्र
हमारे पास समकोण त्रिभुज की भुजाओं का उपयोग करके त्रिकोणमितीय फलनों के मान ज्ञात करने के लिए कुछ सूत्र हैं। इन सूत्रों को लिखने के लिए, हम इन फलनों के संक्षिप्त रूप का उपयोग करते हैं। साइन को , कोसाइन को , स्पर्शज्या को , सेकेंट को , कोसेकेंट को और कोटैंजेंट को लिखा जाता है। त्रिकोणमितीय फलनों को खोजने के लिए मूल सूत्र इस प्रकार हैं:
लंब/कर्ण
आधार/कर्ण
लंब/आधार
कर्ण/आधार
कर्ण/लंब
आधार/लंब
जैसा कि हम ऊपर दिए गए सूत्रों से देख सकते हैं, साइन और कोसेकेंट एक दूसरे के व्युत्क्रम हैं। इसी तरह, व्युत्क्रम युग्म कोसाइन और सेकेंट, तथा स्पर्शरेखा और कोटेंजेंट हैं।
त्रिकोणमितीय फलनों के मान
त्रिकोणमितीय फलनों का एक डोमेन होता है, जो डिग्री या रेडियन में होता है। विभिन्न त्रिकोणमितीय फलनों के लिए के कुछ मुख्य मान नीचे एक तालिका में प्रस्तुत किए गए हैं। इन मुख्य मानों को विशिष्ट कोणों पर त्रिकोणमितीय फलनों के मानक मान के रूप में भी संदर्भित किया जाता है और गणनाओं में प्रायः इनका उपयोग किया जाता है। त्रिकोणमितीय फलनों के मुख्य मान एक इकाई वृत्त से प्राप्त किए गए हैं। ये मान सभी त्रिकोणमितीय सूत्रों को भी संतुष्ट करते हैं।
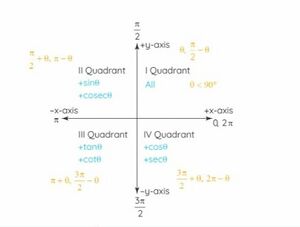
चार चतुर्थांशों में त्रिकोणमितीय फलन
कोण एक न्यून कोण है और इसे धनात्मक -अक्ष के संदर्भ में वामावर्त दिशा में मापा जाता है। इसके अलावा, इन त्रिकोणमितीय फलनों के अलग-अलग चतुर्थांशों में अलग-अलग संख्यात्मक चिह्न ( या ) होते हैं, जो चतुर्थांश के धनात्मक या ऋणात्मक अक्ष पर आधारित होते हैं। के त्रिकोणमितीय फलन चतुर्थांश I और II में धनात्मक हैं, और चतुर्थांश III और IV में ऋणात्मक हैं। सभी त्रिकोणमितीय फलनों की पहली चतुर्थांश में एक धनात्मक सीमा होती है। त्रिकोणमितीय फलन केवल चतुर्थांश I और III में धनात्मक हैं, और के त्रिकोणमितीय अनुपात केवल चतुर्थांश I और IV में धनात्मक हैं।
त्रिकोणमितीय कार्यों के प्रथम चतुर्थांश में , के मान होते हैं। सह-कार्य पहचान कोण के लिए विभिन्न पूरक त्रिकोणमितीय कार्यों के बीच अंतर्संबंध प्रदान करती है।
दूसरे चतुर्थांश में विभिन्न त्रिकोणमितीय कार्यों के लिए डोमेन मान है, तीसरे चतुर्थांश में है, और चौथे चतुर्थांश में है। के लिए त्रिकोणमितीय मान उनके पूरक अनुपातों जैसे कि के रूप में बदलते हैं। के लिए त्रिकोणमितीय मान समान रहते हैं। विभिन्न चतुर्भुजों और कोणों में बदलते त्रिकोणमितीय अनुपातों को नीचे दी गई तालिका से समझा जा सकता है।
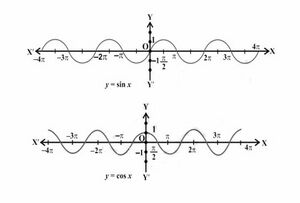
त्रिकोणमितीय फलन ग्राफ
त्रिकोणमितीय फलनों के ग्राफ में का डोमेन मान क्षैतिज -अक्ष पर दर्शाया जाता है और सीमा मान ऊर्ध्वाधर -अक्ष के साथ दर्शाया जाता है। और के ग्राफ मूल बिंदु से होकर गुजरते हैं और अन्य त्रिकोणमितीय फलनों के ग्राफ मूल बिंदु से होकर नहीं गुजरते हैं। और की सीमा तक सीमित है। अनंत मानों की सीमा बिंदीदार रेखाओं के बगल में खींची गई है।