कुछ विशिष्ट फलनों के समाकलन: Difference between revisions
No edit summary |
No edit summary |
||
| (14 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
समाकलन एक विधि है, जो बड़े पैमाने पर फलनों को संक्षेप में प्रस्तुत करती है। इस लेख में, आइए कुछ विशिष्ट [[फलनों के प्रकार|फलनों]] के समाकलन पर चर्चा करें जो साधारणतः गणना के लिए उपयोग किए जाते हैं। इन समाकलन के वास्तविक जीवन में भी कई तरह के अनुप्रयोग हैं, जैसे कि वक्रों के बीच का क्षेत्र ज्ञात करना, आयतन ज्ञात करना, किसी फलन का औसत मान ज्ञात करना, द्रव्यमान का केंद्र, गतिज ऊर्जा, किए गए कार्य की मात्रा, और बहुत कुछ। | |||
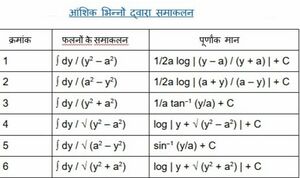
[[Category: | कई महत्वपूर्ण [[समाकलन की विधियाँ|समाकलन]] सूत्र हैं जो कई अन्य मानक समाकलनों को एकीकृत करने के लिए लागू किए जाते हैं। इस लेख में, हम इन विशिष्ट फलनों के समाकलनों पर एक दृष्टि डालेंगे और देखेंगे कि उनका उपयोग कई अन्य मानक समाकलनों में कैसे किया जाता है।[[File:कुछ विशिष्ट फलनों के समाकलन.jpg|thumb|कुछ विशिष्ट फलनों के समाकलन]] | ||
== समाकलन फलनों का प्रमाण == | |||
अब जब आप इन समाकलन फलनों और उनके मूल्यों के बारे में जानते हैं, तो आइए इनमें से प्रत्येक फलन के प्रमाण पर एक दृष्टि डालें। | |||
=== फलन 1 का समाकलन === | |||
<math>\int dy / (y^2- a^2) = 1/2a \log \left\vert (y- a) / (y + a) \right\vert + C</math> | |||
जैसा कि आप जानते हैं, | |||
<math>1 / (y^2 - a^2) = 1 / (y - a) (y + a)</math> | |||
इसका समाधान करते हुए, | |||
<math>= 1/2a(y+a)-(y-a)/(y-a)(y+a)</math> | |||
इसे और कम करते हुए, | |||
<math>= 1/2a\ 1/(y-a)-1/(y+a)</math> | |||
अतः, <math>\int dy / (y^2-a^2) = 1/2a\int dy/(y-a)-\int dy/(y+a)</math> | |||
इसका समाधान करते हुए, | |||
<math>= 1/2a\log \left\vert (y-a)-\log \right\vert (y+a) + C</math> | |||
अत:, | |||
<math>= 1/2a \log \left\vert (y - a) / (y + a) \right\vert + C</math> | |||
=== फलन 2 का समाकलन === | |||
<math>\int dy / (a^2 -y^2) = 1/2a \log \left\vert (a + y) / (a- y) \right\vert + C</math> | |||
जैसा कि आप जानते हैं, | |||
<math>1 / (a^2- y^2) = 1 / (a - y) (a + y)</math> | |||
इसका समाधान करते हुए, | |||
<math>= 1/2a\ (a+y)+(a-y)/(a-y)(a+y)</math> | |||
अत:, | |||
<math>= 1/2a\ 1/(a-y)+1/(a+y)</math> | |||
इसलिए, <math>\int dy / (a^2 -y^2) = 1/2a\int dy/(a-y)+\int dy/(a+y)</math> | |||
जब आप हल करते हैं, | |||
<math>= 1/2a-\log \left\vert (a-y)+\log \right\vert (a+y) + C</math> | |||
अत:, | |||
<math>= 1/2a \log \left\vert (a + y) / (a - y) \right\vert + C</math> | |||
=== फलन 3 का समाकलन === | |||
<math>\int dy / (y^2 + a^2) = 1/a\ tan^{-1} (y/a) + C</math> | |||
<math>y = a \ tan\ t</math> रखने पर, आपको <math>dy = a sec^2\ t\ dt</math> प्राप्त होगा। | |||
इसलिए, | |||
<math>\int dy / (y^2 + a^2) = \int [(a \ sec^2\ t \ dt) / (a^2\ tan^2\ t + a^2)]</math> | |||
इसका समाधान करते हुए, | |||
<math>\int dy / (y^2 + a^2) = 1/a \int dt = t/a + C</math> | |||
<math>t</math> का मान पुनः प्रतिस्थापित करें, | |||
<math>\int dy / (y^2 + a^2) = 1/a\ tan^{-1} (y/a) + C</math> | |||
=== फलन 4 का समाकलन === | |||
<math>\int dy / \sqrt{(y^2 - a^2)} = \log \left\vert y + \sqrt{ (y^2 - a^2)} \right\vert + C</math> | |||
प्रतिस्थापित <math>y = a\ sec\ t</math> | |||
इसलिए, <math>dy = a\ sec\ t\ tan\ t \ dt</math> | |||
इसलिए, | |||
<math>\int dy / \sqrt{(y^2 -a^2)} = \int a\ sec\ t\ tan \ t\ dt / \sqrt{(a^2 sec^2 t - a^2)}</math> | |||
इसका समाधान करते हुए, | |||
<math>\int dy / \sqrt{(y^2 - a^2)} = \int sec\ t\ dt = \log \left\vert sec\ t + tan\ t \right\vert + C_1</math> | |||
<math>t</math> का मान पुनः प्रतिस्थापित करने पर, | |||
<math>\int dy / \sqrt{(y^2 -a^2)} = \log \left\vert (y/a) + \sqrt{[(y^2 -a^2) / a^2]} \right\vert + C_1</math> | |||
इसका समाधान करते हुए, | |||
<math>= \log \left\vert y + \sqrt{(y^2 - a^2)} \right\vert - \log \left\vert a \right\vert + C_1</math> | |||
अत:, | |||
<math>= \log \left\vert y + \sqrt{(y^2-a^2)} \right\vert + C</math> | |||
जहाँ, <math>C = C_1 - \log \left\vert a \right\vert</math> | |||
=== फलन 5 का समाकलन === | |||
<math>\int dy / \sqrt{ (a^2- y^2)} = sin^{-1} (y/a) + C</math> | |||
प्रतिस्थापन करने पर <math>y = a \ sin \ t</math> | |||
<math>dy = a \ cos \ t\ dt</math> | |||
इसलिए, | |||
<math>\int dy / \sqrt{(a^2 -y^2)} = \int a\ cos\ t \ dt / {\sqrt{(a^2 -a^2 sin^2 t)}}</math> | |||
इसका समाधान करते हुए, | |||
<math>\int dy / \sqrt{(a^2 - y^2)} = \int t\ dt = t + C</math> | |||
<math>t</math> का मान पुनः प्रतिस्थापित करें, | |||
<math>\int dy / \sqrt{(a^2 -y^2)} = sin^{-1} (y/a) + C</math> | |||
=== फलन 6 का समाकलन === | |||
<math>\int dy / \sqrt{(y^2 + a^2)} = \log \left\vert y + \sqrt{(y^2 + a^2)} \right\vert + C</math> | |||
प्रतिस्थापन करने पर <math>y = a \ tan\ t,</math> | |||
<math>dy = a sec^2\ t\ dt</math> | |||
इसलिए, | |||
<math>\int dy / \sqrt{(y^2 + a^2)} = \int a sec^2 t dt / \sqrt{(a^2 tan^2t + a^2)}</math> | |||
इसका समाधान करते हुए, | |||
<math>\int dy / \sqrt{(y^2 - a^2)} = \int sec \ t \ dt = \log \left\vert sec\ t + tan\ t \right\vert + C_1</math> | |||
<math>t</math> का मान पुनः प्रतिस्थापित करें, | |||
<math>\int dy / \sqrt{(y^2 - a^2)} = \log \left\vert (y/a) + \sqrt{[(y^2 + a^2) / a^2]} \right\vert + C_1</math> | |||
इसका समाधान करते हुए, | |||
<math>= \log \left\vert y + \sqrt{(y2 + a2)} \right\vert-\log\left\vert a \right\vert + C_1</math> | |||
अत:, | |||
<math>= \log \left\vert y + \sqrt{(y^2 + a^2)} \right\vert + C</math> | |||
जहाँ, <math>C = C_1 - \log \left\vert a \right\vert</math> | |||
=== फलन 7 का समाकलन === | |||
<math>\int dy / (ay^2 + by + c)</math> | |||
आप इसे इस प्रकार लिख सकते हैं | |||
<math>ay^2 + by + c = a [y^2 + (b/a)y + (c/a)]</math> | |||
इसका समाधान करते हुए, | |||
<math>a [(y + b/2a)^2 + (c/a- b^2/4a^2)]</math> | |||
प्रतिस्थापित करें <math>(y + b/2a) = t</math> और आपको <math>dy = dt</math> प्राप्त होगा । | |||
प्रतिस्थापन <math>(c/a - b^2/4a^2) = \pm k^2</math>। | |||
इसलिए, | |||
<math>ay^2 + by + c = a (t^2 \pm k^2)</math> | |||
जहाँ + या – चिह्न समीकरण <math>(c/a - b^2/4a^2)</math> के चिह्न पर निर्भर करते हैं. | |||
इसलिए, | |||
<math>\int dy / (ay^2 + by + c) = 1/a \int dt / (t^2 \pm k^2)</math> | |||
आप ऊपर दिखाए गए siy एकीकरण सूत्रों में से एक या अधिक का उपयोग करके इस समीकरण का मूल्यांकन कर सकते हैं। याद रखें कि आप इसी तरह से समीकरण <math>\int dy / \sqrt{(ay^2 + by + c)}</math> को भी हल कर सकते हैं। | |||
=== फलन 8 का समाकलन === | |||
∫ [(py + q) / (ay<sup>2</sup> + by + c)] dy, | |||
जहाँ <math>p, q, a, b, c</math> स्थिरांक माने जाते हैं। | |||
इसे हल करने के लिए, आपको स्थिरांक <math>A</math> और <math>B</math> ज्ञात करने होंगे, जैसे कि, | |||
<math>(py + q) = A d/dy (ay^2 + by + c) + B,</math> जो <math>= A (2ay + b) + B</math> बराबर है | |||
‘<math>A</math>’ और ‘<math>B</math>’ निर्धारित करने के लिए, सबसे पहले, y के गुणांकों और स्थिर पदों के दोनों ओर से समान करें। तब ‘<math>A</math>’ और ‘<math>B</math>’ प्राप्त किए जा सकते हैं और इसलिए, समाकल को ज्ञात रूपों में से किसी एक में घटाया जा सकता है। | |||
== उदाहरण == | |||
<math>y</math> के सापेक्ष <math>(y + 3) / \sqrt{ (5 - 4y + y^2)}</math> का समाकल ज्ञात कीजिए। | |||
समाधान | |||
आप अभिव्यक्त कर सकते हैं | |||
<math>y + 3 = A d/dy (5 - 4y + y^2) + B = A (- 4 - 2y) + B</math> | |||
गुणांकों को समान करने पर, आपको प्राप्त होता है | |||
<math>A = -{1 \over 2}</math> and <math>B = 1</math> | |||
इसलिए, | |||
<math>\int [(y + 3) / \sqrt{(5 -4y + y^2)}] dy = -{1 \over 2} \int [(- 4 - 2y) / \sqrt{(5 - 4y + y^2)]} dy + \int dy / \sqrt{(5 - 4y + y^2)}</math> | |||
<math>= -{1 \over 2} I_1 + I_2... (a)</math> | |||
इसका समाधान करते हुए, <math>I_1</math> | |||
प्रतिस्थापन <math>(5 -4y + y^2) = t,</math> | |||
<math>(- 4 -2y) dy = dt</math> | |||
इसलिए, | |||
<math>I_1 = \int [(- 4- 2y) / \sqrt{(5 - 4y + y^2)}] dy = \int dt / \sqrt{t} = 2 \sqrt{t} + C_1</math> | |||
<math>= 2 \sqrt{(5 - 4y + y^2)} + C1...(b)</math> | |||
इसका समाधान करते हुए, <math>I_2</math> | |||
<math>I_2 = \int dy / \sqrt{ (5 - 4y + y^2)} =</math> | |||
<math>\int dy / \sqrt{[9 - (y + 2)^2}]</math> | |||
प्रतिस्थापन करते हुए <math>(y + 2) = t,</math> | |||
<math>dy = dt</math> | |||
इसलिए, | |||
<math>I_2 = \int dt / \sqrt{ (3^2 - t^2)} = sin^{-1} (t/3) + C_2</math> | |||
इसका समाधान करते हुए, | |||
<math>= sin^{-1}(y+2)/3 + C_2... (c)</math> | |||
<math>(a)</math> के स्थान पर <math>(b)</math> और <math>(c)</math> प्रतिस्थापन करने पर , | |||
<math>\int [(y + 3) / \sqrt{(5 - 4y + y^2)}] dy = -{1 \over 2} I_1 + I_2</math> | |||
<math>= -\sqrt{(5 -4y + y^2)} + sin^{-1} + C</math> | |||
जहाँ <math>C = C_2 = C_1/2</math> | |||
[[Category:समाकलन]][[Category:गणित]][[Category:कक्षा-12]] | |||
Latest revision as of 17:59, 5 December 2024
समाकलन एक विधि है, जो बड़े पैमाने पर फलनों को संक्षेप में प्रस्तुत करती है। इस लेख में, आइए कुछ विशिष्ट फलनों के समाकलन पर चर्चा करें जो साधारणतः गणना के लिए उपयोग किए जाते हैं। इन समाकलन के वास्तविक जीवन में भी कई तरह के अनुप्रयोग हैं, जैसे कि वक्रों के बीच का क्षेत्र ज्ञात करना, आयतन ज्ञात करना, किसी फलन का औसत मान ज्ञात करना, द्रव्यमान का केंद्र, गतिज ऊर्जा, किए गए कार्य की मात्रा, और बहुत कुछ।
कई महत्वपूर्ण समाकलन सूत्र हैं जो कई अन्य मानक समाकलनों को एकीकृत करने के लिए लागू किए जाते हैं। इस लेख में, हम इन विशिष्ट फलनों के समाकलनों पर एक दृष्टि डालेंगे और देखेंगे कि उनका उपयोग कई अन्य मानक समाकलनों में कैसे किया जाता है।
समाकलन फलनों का प्रमाण
अब जब आप इन समाकलन फलनों और उनके मूल्यों के बारे में जानते हैं, तो आइए इनमें से प्रत्येक फलन के प्रमाण पर एक दृष्टि डालें।
फलन 1 का समाकलन
जैसा कि आप जानते हैं,
इसका समाधान करते हुए,
इसे और कम करते हुए,
अतः,
इसका समाधान करते हुए,
अत:,
फलन 2 का समाकलन
जैसा कि आप जानते हैं,
इसका समाधान करते हुए,
अत:,
इसलिए,
जब आप हल करते हैं,
अत:,
फलन 3 का समाकलन
रखने पर, आपको प्राप्त होगा।
इसलिए,
इसका समाधान करते हुए,
का मान पुनः प्रतिस्थापित करें,
फलन 4 का समाकलन
प्रतिस्थापित
इसलिए,
इसलिए,
इसका समाधान करते हुए,
का मान पुनः प्रतिस्थापित करने पर,
इसका समाधान करते हुए,
अत:,
जहाँ,
फलन 5 का समाकलन
प्रतिस्थापन करने पर
इसलिए,
इसका समाधान करते हुए,
का मान पुनः प्रतिस्थापित करें,
फलन 6 का समाकलन
प्रतिस्थापन करने पर
इसलिए,
इसका समाधान करते हुए,
का मान पुनः प्रतिस्थापित करें,
इसका समाधान करते हुए,
अत:,
जहाँ,
फलन 7 का समाकलन
आप इसे इस प्रकार लिख सकते हैं
इसका समाधान करते हुए,
प्रतिस्थापित करें और आपको प्राप्त होगा ।
प्रतिस्थापन ।
इसलिए,
जहाँ + या – चिह्न समीकरण के चिह्न पर निर्भर करते हैं.
इसलिए,
आप ऊपर दिखाए गए siy एकीकरण सूत्रों में से एक या अधिक का उपयोग करके इस समीकरण का मूल्यांकन कर सकते हैं। याद रखें कि आप इसी तरह से समीकरण को भी हल कर सकते हैं।
फलन 8 का समाकलन
∫ [(py + q) / (ay2 + by + c)] dy,
जहाँ स्थिरांक माने जाते हैं।
इसे हल करने के लिए, आपको स्थिरांक और ज्ञात करने होंगे, जैसे कि,
जो बराबर है
‘’ और ‘’ निर्धारित करने के लिए, सबसे पहले, y के गुणांकों और स्थिर पदों के दोनों ओर से समान करें। तब ‘’ और ‘’ प्राप्त किए जा सकते हैं और इसलिए, समाकल को ज्ञात रूपों में से किसी एक में घटाया जा सकता है।
उदाहरण
के सापेक्ष का समाकल ज्ञात कीजिए।
समाधान
आप अभिव्यक्त कर सकते हैं
गुणांकों को समान करने पर, आपको प्राप्त होता है
and
इसलिए,
इसका समाधान करते हुए,
प्रतिस्थापन
इसलिए,
इसका समाधान करते हुए,
प्रतिस्थापन करते हुए
इसलिए,
इसका समाधान करते हुए,
के स्थान पर और प्रतिस्थापन करने पर ,
जहाँ