शंकु के परिच्छेद: Difference between revisions
(added category) |
No edit summary |
||
| (19 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
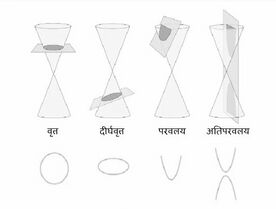
शंकु खंड या शंकु के परिच्छेद, एक समतल और शंकु के प्रतिच्छेदन द्वारा प्राप्त वक्र हैं। शंकु या शंकु के परिच्छेद के तीन प्रमुख परिच्छेद हैं: परवलय, अतिपरवलय और दीर्घवृत्त ([[वृत्त]] एक विशेष प्रकार का दीर्घवृत्त है)। शंकु के परिच्छेद का निर्माण करने के लिए दो समान नैप्स (nappes) वाले शंकु का उपयोग किया जाता है। | |||
[[ | शंकु या शंकु के परिच्छेद के सभी परिच्छेदों के आकार अलग-अलग होते हैं, लेकिन उनमें कुछ सामान्य गुण होते हैं, जिनके बारे में हम निम्नलिखित अनुभागों में पढ़ेंगे। | ||
[[Category:शंकु परिच्छेद]] | |||
== परिभाषा == | |||
शंकु के परिच्छेद वे वक्र हैं जो तब प्राप्त होते हैं जब एक समतल शंकु से गुजरता है। एक शंकु में साधारणतः दो समान शंक्वाकार आकृतियाँ होती हैं जिन्हें नैप्स कहा जाता है। समतल और शंकु तथा उसके नैप्स के बीच कट के कोण के आधार पर हम विभिन्न आकृतियाँ प्राप्त कर सकते हैं। एक शंकु को समतल द्वारा विभिन्न कोणों पर काटने पर, हमें निम्नलिखित आकृतियाँ प्राप्त होती हैं: | |||
* वृत्त | |||
* परवलय | |||
* दीर्घवृत्त | |||
* अतिपरवलय | |||
दीर्घवृत्त एक शंकु परिच्छेद है जो तब बनता है जब एक समतल शंकु को एक कोण पर काटता है। वृत्त एक विशेष प्रकार का दीर्घवृत्त है जहाँ काटने वाला समतल शंकु के आधार के समानांतर होता है। अतिपरवलय(हाइपरबोला) तब बनता है जब प्रभावशाली समतल शंकु की धुरी के समानांतर होता है और दोहरे शंकु के दोनों नैप्स को काटता है। जब प्रतिच्छेद करने वाला समतल शंकु की सतह को एक कोण पर काटता है, तो हमें परवलय नामक एक शंकु परिच्छेद मिलता है। | |||
[[File:शंकु के परिच्छेद.jpg|thumb|276x276px|चित्र- शंकु के परिच्छेद]] | |||
== शंकु के परिच्छेद मापदंड == | |||
नाभि(फोकस), नियता(डायरेक्ट्रिक्स) और [[उत्केन्द्रता]](एक्सेंट्रिसिटी) तीन महत्वपूर्ण विशेषताएं या पैरामीटर हैं जो शंकु को परिभाषित करते हैं। विभिन्न शंकु आकृतियाँ वृत्त, [[दीर्घवृत्त]], [[परवलय]] और [[अतिपरवलय]] हैं। इन आकृतियों का आकार और अभिविन्यास(ओरिएंटेशन) पूरी तरह से इन तीन महत्वपूर्ण विशेषताओं पर आधारित है। | |||
== शंकु के परिच्छेद सूत्र == | |||
यहाँ दी गई तालिका में शंकु के विभिन्न प्रकार के अनुभागों के लिए सूत्र देखें। | |||
{| class="wikitable" | |||
|वृत्त | |||
|केंद्र <math>(a, b)</math> है | |||
त्रिज्या <math>r</math> है | |||
|<math>(x-a)^2+(y-b)^2=r^2</math> | |||
|- | |||
|क्षैतिज दीर्घ अक्ष के साथ दीर्घवृत्त | |||
|केंद्र <math>(a, b)</math> है | |||
दीर्घ अक्ष की लंबाई <math>2h</math> है। लघु अक्ष की लंबाई <math>2k</math> है। केंद्र और किसी भी नाभि के बीच की दूरी <math>c</math> है जिसमें <math>c^2=h^2-k^2, h>k>0</math> है | |||
|<math>\frac{(x-a)^2}{h^2}+\frac{(y-b)^2}{k^2} =1</math> | |||
|- | |||
|ऊर्ध्वाधर दीर्घ अक्ष के साथ दीर्घवृत्त | |||
|केंद्र <math>(a, b)</math> है | |||
दीर्घ अक्ष की लंबाई <math>2h</math> है। लघु अक्ष की लंबाई <math>2k</math> है। केंद्र और किसी भी नाभि के बीच की दूरी <math>c</math> है जिसमें <math>c^2=h^2-k^2, h>k>0</math> है | |||
|<math>\frac{(x-a)^2}{k^2}+\frac{(y-b)^2}{h^2} =1</math> | |||
|- | |||
|क्षैतिज अनुप्रस्थ अक्ष के साथ अतिपरवलय | |||
|केंद्र <math>(a, b)</math> है | |||
शीर्षों के बीच की दूरी <math>2h</math> है | |||
नाभियों के बीच की दूरी <math>2k</math> है। | |||
<math>c^2=h^2+k^2</math> | |||
|<math>\frac{(x-a)^2}{h^2}-\frac{(y-b)^2}{k^2} =1</math> | |||
|- | |||
|ऊर्ध्वाधर अनुप्रस्थ अक्ष के साथ अतिपरवलय | |||
|केंद्र <math>(a, b)</math> है | |||
शीर्षों के बीच की दूरी <math>2h</math> है | |||
नाभियों के बीच की दूरी <math>2k</math> है। | |||
<math>c^2=h^2+k^2</math> | |||
|<math>\frac{(x-a)^2}{k^2}-\frac{(y-b)^2}{h^2} =1</math> | |||
|- | |||
|क्षैतिज अक्ष के साथ परवलय | |||
|शीर्ष <math>(a, b)</math> है | |||
नाभि <math>(a+p,b)</math> है | |||
नियता रेखा है | |||
<math>x=a-p</math> | |||
अक्ष रेखा है <math>y=b</math> | |||
|<math>(y-b)^2=4p(x-a), p\neq0</math> | |||
|- | |||
|ऊर्ध्वाधर अक्ष के साथ परवलय | |||
|शीर्ष <math>(a, b)</math> है | |||
नाभि <math>(a+p,b)</math> है | |||
नियता रेखा है | |||
<math>x=b-p</math> | |||
अक्ष रेखा है <math>x=a</math> | |||
|<math>(x-a)^2=4p(y-b), p\neq0</math> | |||
|} | |||
== शंकु के परिच्छेद से संबंधित शब्द == | |||
इन तीन मापदंडों के अलावा, शंकु खंडों में कुछ और मापदंड होते हैं जैसे कि मुख्य अक्ष(प्रिंसिपल एक्सिस), [[नाभिलंब जीवा]](लेटस रेक्टम), दीर्घ अक्ष(मेजर एक्सिस) और लघु अक्ष(माइनर एक्सिस), नाभीय प्राचल (फोकल पैरामीटर), आदि। आइए शंकु परिच्छेद से संबंधित इन मापदंडों में से प्रत्येक के बारे में संक्षेप में जानें। शंकु परिच्छेद के मापदंडों का विवरण निम्नलिखित है। | |||
* '''दीर्घ अक्ष''': शंकु के केंद्र और नाभियों से गुजरने वाली अक्ष इसकी मुख्य अक्ष होती है और इसे शंकु की दीर्घ अक्ष भी कहा जाता है। | |||
* '''संयुग्मी अक्ष''': मुख्य अक्ष के लंबवत खींची गई अक्ष और शंकु के केंद्र से गुजरने वाली अक्ष संयुग्मी अक्ष होती है। संयुग्मी अक्ष इसकी लघु अक्ष भी होती है। | |||
* '''केंद्र''': शंकु की मुख्य अक्ष और संयुग्मी अक्ष के प्रतिच्छेद बिंदु को शंकु का केंद्र कहा जाता है। | |||
* '''शीर्ष''': अक्ष पर वह बिंदु जहाँ शंकु अक्ष को काटता है, शंकु का शीर्ष कहलाता है। | |||
* '''नाभीय जीवा''' : शंकु की नाभीय जीवा शंकु खंड के नाभि से गुजरने वाली जीवा होती है। नाभीय जीवा शंकु के परिच्छेद को दो अलग-अलग बिंदुओं पर काटती है। | |||
* '''फोकल दूरी''': शंकु पर किसी बिंदु <math>(x_1,y_1)</math> की किसी भी नाभियों से दूरी, नाभीय दूरी होती है। दीर्घवृत्त, अतिपरवलय के लिए हमारे पास दो नाभि होते हैं, और इसलिए हमारे पास दो नाभीय दूरियाँ होती हैं। | |||
* '''नाभिलंब जीवा''': यह एक नाभीय जीवा है जो शंकु की धुरी के लंबवत होती है। परवलय के लिए नाभिलंब जीवा की लंबाई <math>LL' = 4a</math> है। और दीर्घवृत्त और अतिपरवलय के लिए नाभिलंब जीवा की लंबाई <math> \frac{2b^2}{a}</math> है। | |||
* '''स्पर्शरेखा''': स्पर्शरेखा एक रेखा है जो शंकु पर एक बिंदु पर बाहरी रूप से शंकु को छूती है। वह बिंदु जहाँ स्पर्शरेखा शंकु को छूती है उसे संपर्क बिंदु कहा जाता है। साथ ही बाहरी बिंदु से, शंकु पर लगभग दो स्पर्शरेखाएँ खींची जा सकती हैं। | |||
* '''सामान्य''': स्पर्शरेखा के लंबवत खींची गई रेखा और संपर्क बिंदु और शंकु के नाभियों से गुज़रने वाली रेखा को सामान्य कहा जाता है। हम शंकु पर प्रत्येक स्पर्शरेखा के लिए एक सामान्य रख सकते हैं। | |||
* '''संपर्क जीवा''': बाहरी बिंदु से शंकु तक खींची गई स्पर्श रेखाओं के संपर्क बिंदु को जोड़ने के लिए जीवा खींची जाती है, जिसे संपर्क जीवा कहते हैं। | |||
* '''ध्रुवीय और ध्रुवीय''': एक बिंदु के लिए जिसे ध्रुव कहा जाता है और शंकु खंड के बाहर स्थित होता है, इस बिंदु से खींची गई जीवाओं के सिरों पर खींची गई स्पर्श रेखाओं के प्रतिच्छेद बिंदुओं के बिन्दुपथ को ध्रुवीय कहते हैं। | |||
* '''सहायक वृत्त''': दीर्घवृत्त के प्रमुख अक्ष पर एक वृत्त खींचा जाता है क्योंकि इसका व्यास सहायक वृत्त कहलाता है। दीर्घवृत्त का शंकु समीकरण <math> \frac{x^2}{a^2}+ \frac{y^2}{b^2} = 1</math> है, और सहायक वृत्त का समीकरण <math>x^2 + y^2 = a^2</math> है। | |||
* '''निर्देशक वृत्त''': दीर्घवृत्त पर खींची गई लंबवत स्पर्श रेखाओं के प्रतिच्छेद बिंदु के बिन्दुपथ को निदेशक वृत्त कहते हैं। एक दीर्घवृत्त | |||
<math> \Bigl(\frac{x^2}{a^2}+ \frac{y^2}{b^2} = 1\Bigr)</math> के लिए, निर्देशक वृत्त का समीकरण <math>x^2 + y^2 = a^2+b^2</math> है | |||
* '''अस्पर्शी''': अतिपरवलय के समानांतर खींची गई सीधी रेखाओं की जोड़ी और माना जाता है कि वे अनंत पर अतिपरवलय को छूती हैं। अतिपरवलय के अस्पर्शी के समीकरण क्रमशः<math>y = \frac{bx}{a}</math>, और <math>y = \frac{-bx}{a}</math> हैं। और एक अतिपरवलय के लिए जिसका शंकु समीकरण<math> \frac{x^2}{a^2}+ \frac{y^2}{b^2} = 1</math> है, अतिपरवलय के अस्पर्शी के जोड़े का समीकरण <math>\frac{x}{a}\pm \frac{y}{b}=0</math> है। | |||
[[Category:शंकु परिच्छेद]][[Category:कक्षा-11]][[Category:गणित]] | |||
Latest revision as of 19:49, 22 November 2024
शंकु खंड या शंकु के परिच्छेद, एक समतल और शंकु के प्रतिच्छेदन द्वारा प्राप्त वक्र हैं। शंकु या शंकु के परिच्छेद के तीन प्रमुख परिच्छेद हैं: परवलय, अतिपरवलय और दीर्घवृत्त (वृत्त एक विशेष प्रकार का दीर्घवृत्त है)। शंकु के परिच्छेद का निर्माण करने के लिए दो समान नैप्स (nappes) वाले शंकु का उपयोग किया जाता है।
शंकु या शंकु के परिच्छेद के सभी परिच्छेदों के आकार अलग-अलग होते हैं, लेकिन उनमें कुछ सामान्य गुण होते हैं, जिनके बारे में हम निम्नलिखित अनुभागों में पढ़ेंगे।
परिभाषा
शंकु के परिच्छेद वे वक्र हैं जो तब प्राप्त होते हैं जब एक समतल शंकु से गुजरता है। एक शंकु में साधारणतः दो समान शंक्वाकार आकृतियाँ होती हैं जिन्हें नैप्स कहा जाता है। समतल और शंकु तथा उसके नैप्स के बीच कट के कोण के आधार पर हम विभिन्न आकृतियाँ प्राप्त कर सकते हैं। एक शंकु को समतल द्वारा विभिन्न कोणों पर काटने पर, हमें निम्नलिखित आकृतियाँ प्राप्त होती हैं:
- वृत्त
- परवलय
- दीर्घवृत्त
- अतिपरवलय
दीर्घवृत्त एक शंकु परिच्छेद है जो तब बनता है जब एक समतल शंकु को एक कोण पर काटता है। वृत्त एक विशेष प्रकार का दीर्घवृत्त है जहाँ काटने वाला समतल शंकु के आधार के समानांतर होता है। अतिपरवलय(हाइपरबोला) तब बनता है जब प्रभावशाली समतल शंकु की धुरी के समानांतर होता है और दोहरे शंकु के दोनों नैप्स को काटता है। जब प्रतिच्छेद करने वाला समतल शंकु की सतह को एक कोण पर काटता है, तो हमें परवलय नामक एक शंकु परिच्छेद मिलता है।
शंकु के परिच्छेद मापदंड
नाभि(फोकस), नियता(डायरेक्ट्रिक्स) और उत्केन्द्रता(एक्सेंट्रिसिटी) तीन महत्वपूर्ण विशेषताएं या पैरामीटर हैं जो शंकु को परिभाषित करते हैं। विभिन्न शंकु आकृतियाँ वृत्त, दीर्घवृत्त, परवलय और अतिपरवलय हैं। इन आकृतियों का आकार और अभिविन्यास(ओरिएंटेशन) पूरी तरह से इन तीन महत्वपूर्ण विशेषताओं पर आधारित है।
शंकु के परिच्छेद सूत्र
यहाँ दी गई तालिका में शंकु के विभिन्न प्रकार के अनुभागों के लिए सूत्र देखें।
| वृत्त | केंद्र है
त्रिज्या है |
|
| क्षैतिज दीर्घ अक्ष के साथ दीर्घवृत्त | केंद्र है
दीर्घ अक्ष की लंबाई है। लघु अक्ष की लंबाई है। केंद्र और किसी भी नाभि के बीच की दूरी है जिसमें है |
|
| ऊर्ध्वाधर दीर्घ अक्ष के साथ दीर्घवृत्त | केंद्र है
दीर्घ अक्ष की लंबाई है। लघु अक्ष की लंबाई है। केंद्र और किसी भी नाभि के बीच की दूरी है जिसमें है |
|
| क्षैतिज अनुप्रस्थ अक्ष के साथ अतिपरवलय | केंद्र है
शीर्षों के बीच की दूरी है नाभियों के बीच की दूरी है।
|
|
| ऊर्ध्वाधर अनुप्रस्थ अक्ष के साथ अतिपरवलय | केंद्र है
शीर्षों के बीच की दूरी है नाभियों के बीच की दूरी है।
|
|
| क्षैतिज अक्ष के साथ परवलय | शीर्ष है
नाभि है नियता रेखा है
अक्ष रेखा है |
|
| ऊर्ध्वाधर अक्ष के साथ परवलय | शीर्ष है
नाभि है नियता रेखा है
अक्ष रेखा है |
शंकु के परिच्छेद से संबंधित शब्द
इन तीन मापदंडों के अलावा, शंकु खंडों में कुछ और मापदंड होते हैं जैसे कि मुख्य अक्ष(प्रिंसिपल एक्सिस), नाभिलंब जीवा(लेटस रेक्टम), दीर्घ अक्ष(मेजर एक्सिस) और लघु अक्ष(माइनर एक्सिस), नाभीय प्राचल (फोकल पैरामीटर), आदि। आइए शंकु परिच्छेद से संबंधित इन मापदंडों में से प्रत्येक के बारे में संक्षेप में जानें। शंकु परिच्छेद के मापदंडों का विवरण निम्नलिखित है।
- दीर्घ अक्ष: शंकु के केंद्र और नाभियों से गुजरने वाली अक्ष इसकी मुख्य अक्ष होती है और इसे शंकु की दीर्घ अक्ष भी कहा जाता है।
- संयुग्मी अक्ष: मुख्य अक्ष के लंबवत खींची गई अक्ष और शंकु के केंद्र से गुजरने वाली अक्ष संयुग्मी अक्ष होती है। संयुग्मी अक्ष इसकी लघु अक्ष भी होती है।
- केंद्र: शंकु की मुख्य अक्ष और संयुग्मी अक्ष के प्रतिच्छेद बिंदु को शंकु का केंद्र कहा जाता है।
- शीर्ष: अक्ष पर वह बिंदु जहाँ शंकु अक्ष को काटता है, शंकु का शीर्ष कहलाता है।
- नाभीय जीवा : शंकु की नाभीय जीवा शंकु खंड के नाभि से गुजरने वाली जीवा होती है। नाभीय जीवा शंकु के परिच्छेद को दो अलग-अलग बिंदुओं पर काटती है।
- फोकल दूरी: शंकु पर किसी बिंदु की किसी भी नाभियों से दूरी, नाभीय दूरी होती है। दीर्घवृत्त, अतिपरवलय के लिए हमारे पास दो नाभि होते हैं, और इसलिए हमारे पास दो नाभीय दूरियाँ होती हैं।
- नाभिलंब जीवा: यह एक नाभीय जीवा है जो शंकु की धुरी के लंबवत होती है। परवलय के लिए नाभिलंब जीवा की लंबाई है। और दीर्घवृत्त और अतिपरवलय के लिए नाभिलंब जीवा की लंबाई है।
- स्पर्शरेखा: स्पर्शरेखा एक रेखा है जो शंकु पर एक बिंदु पर बाहरी रूप से शंकु को छूती है। वह बिंदु जहाँ स्पर्शरेखा शंकु को छूती है उसे संपर्क बिंदु कहा जाता है। साथ ही बाहरी बिंदु से, शंकु पर लगभग दो स्पर्शरेखाएँ खींची जा सकती हैं।
- सामान्य: स्पर्शरेखा के लंबवत खींची गई रेखा और संपर्क बिंदु और शंकु के नाभियों से गुज़रने वाली रेखा को सामान्य कहा जाता है। हम शंकु पर प्रत्येक स्पर्शरेखा के लिए एक सामान्य रख सकते हैं।
- संपर्क जीवा: बाहरी बिंदु से शंकु तक खींची गई स्पर्श रेखाओं के संपर्क बिंदु को जोड़ने के लिए जीवा खींची जाती है, जिसे संपर्क जीवा कहते हैं।
- ध्रुवीय और ध्रुवीय: एक बिंदु के लिए जिसे ध्रुव कहा जाता है और शंकु खंड के बाहर स्थित होता है, इस बिंदु से खींची गई जीवाओं के सिरों पर खींची गई स्पर्श रेखाओं के प्रतिच्छेद बिंदुओं के बिन्दुपथ को ध्रुवीय कहते हैं।
- सहायक वृत्त: दीर्घवृत्त के प्रमुख अक्ष पर एक वृत्त खींचा जाता है क्योंकि इसका व्यास सहायक वृत्त कहलाता है। दीर्घवृत्त का शंकु समीकरण है, और सहायक वृत्त का समीकरण है।
- निर्देशक वृत्त: दीर्घवृत्त पर खींची गई लंबवत स्पर्श रेखाओं के प्रतिच्छेद बिंदु के बिन्दुपथ को निदेशक वृत्त कहते हैं। एक दीर्घवृत्त
के लिए, निर्देशक वृत्त का समीकरण है
- अस्पर्शी: अतिपरवलय के समानांतर खींची गई सीधी रेखाओं की जोड़ी और माना जाता है कि वे अनंत पर अतिपरवलय को छूती हैं। अतिपरवलय के अस्पर्शी के समीकरण क्रमशः, और हैं। और एक अतिपरवलय के लिए जिसका शंकु समीकरण है, अतिपरवलय के अस्पर्शी के जोड़े का समीकरण है।