सदिशों का योगफल: Difference between revisions

Latest revision as of 15:56, 10 December 2024

सदिशों का योगफल का अनुप्रयोग भौतिक राशियों में होता है जहाँ सदिश का उपयोग वेग, विस्थापन और त्वरण को दर्शाने के लिए किया जाता है।

सदिशों को ज्यामितीय रूप से जोड़ना उनकी अन्त्य बिंदुओं को एक साथ रखना है और इस प्रकार एक समांतर चतुर्भुज का निर्माण करना है। सदिशों का योग समांतर चतुर्भुज का विकर्ण होता है जो अन्त्य के प्रतिच्छेदन से प्रारंभ होता है।
बीजगणितीय रूप से सदिशों को जोड़ना उनके संगत अवयवों को जोड़ना है।

इस लेख में, आइए हल किए गए उदाहरणों के साथ सदिशों के योग, उनके गुणों और विभिन्न नियमों के बारे में जानें।

परिभाषा

सदिश को दिशा और परिमाण के संयोजन के रूप में दर्शाया जाता है और उन्हें एक वर्णमाला और उनके ऊपर एक बाण चिन्ह (या) बोल्ड में लिखे गए वर्णमाला के साथ लिखा जाता है। दो सदिशों, $a$ और $b,$ को सदिश जोड़ का उपयोग करके एक साथ जोड़ा जा सकता है, और परिणामी सदिश को इस प्रकार लिखा जा सकता है: $a+b$ । सदिश जोड़ के गुणों के बारे में जानने से पहले, हमें उन शर्तों के बारे में जानना होगा जिनका सदिश जोड़ते समय पालन किया जाना चाहिए।

शर्तें इस प्रकार हैं:

सदिशों को तभी जोड़ा जा सकता है जब वे एक ही स्वरूप के हों। उदाहरण के लिए, त्वरण को केवल त्वरण के साथ जोड़ा जाना चाहिए, द्रव्यमान के साथ नहीं
हम सदिशों और अदिशों को एक साथ नहीं जोड़ सकते

दो सदिशों $C$ और $D$ पर विचार करें, जहाँ, C $=C_{x}i+C_{y}j+C_{z}k$ और D $=D_{x}i+D_{y}j+D_{z}k$ । फिर, परिणामी सदिश (या सदिश योग सूत्र) R = C + D $=(C_{x}+D_{x})i+(C_{y}+D_{y})j+(C_{z}+C_{z})k$ है

सदिशों का योगफल के गुण

सदिश जोड़ बीजीय जोड़ से अलग है। सदिश जोड़ करते समय विचार किए जाने वाले कुछ महत्वपूर्ण गुण यहां दिए गए हैं:


सदिशों का योगफल के गुण	स्पष्टीकरण
तत्समक का अस्तित्व	किसी भी सदिश v के लिए , v + 0 = v यहाँ, 0 सदिश योगात्मक पहचान है।
व्युत्क्रम का अस्तित्व	किसी भी सदिश v के लिए , v + - v = 0 और इस प्रकार प्रत्येक सदिश के लिए एक योज्य व्युत्क्रम उपस्थित होता है।
क्रम विनिमेयता	योग क्रमविनिमेय है; किसी भी दो स्वेच्छ सदिश c,और d, के लिए, c + d = d + c
साहचर्यता	योग क्रमविनिमेय है; किसी भी तीन स्वेच्छ सदिश i,j और k के लिए i + j + k = i + j + k अर्थात, जोड़ने का क्रम मायने नहीं रखता

सदिशों का आलेखीय रूप से योगफल

सदिशों का योगफल ग्राफिकल और गणितीय विधियों का उपयोग करके किया जा सकता है। ये विधियाँ इस प्रकार हैं:

अवयवों का उपयोग करके सदिश योगफल
सदिशों के योगफल का त्रिभुज नियम
सदिशों के योगफल का समांतर चतुर्भुज नियम

सदिशों का योगफल

अवयवों का उपयोग करके सदिशों का योगफल

कार्टेशियन निर्देशांक में दर्शाए गए सदिश को ऊर्ध्वाधर और क्षैतिज अवयवों में विघटित किया जा सकता है। उदाहरण के लिए, नीचे दी गई छवि में दिखाए गए कोण $\phi$ पर एक सदिश $A$ को इसके ऊर्ध्वाधर और क्षैतिज अवयवों में विघटित किया जा सकता है:

उपरोक्त छवि में,

Ax, क्षैतिज अक्ष ( $x$ -अक्ष) के साथ सदिश $A$ के अवयव को दर्शाता है, और

Ay, ऊर्ध्वाधर अक्ष ( $y$ -अक्ष) के साथ सदिश $A$ के अवयव को दर्शाता है।

हम देख सकते हैं कि तीनों सदिश एक समकोण त्रिभुज बनाते हैं और सदिश $A$ को इस प्रकार व्यक्त किया जा सकता है:

A = Ax + Ay

गणितीय रूप से, दिए गए सदिश के परिमाण और कोण का उपयोग करके, हम सदिश के अवयवों को निर्धारित कर सकते हैं।

Ax $=A\ cos\phi$

Ay $=A\ sin\phi$

दो सदिशों के लिए, यदि उनके क्षैतिज और ऊर्ध्वाधर अवयव दिए गए हैं, तो परिणामी सदिश की गणना की जा सकती है। उदाहरण के लिए, यदि Ax और Ay के मान दिए गए हैं, तो हम सदिश $A$ के कोण और परिमाण की गणना इस प्रकार कर पाएंगे:

$|A|={\sqrt {((A_{x})^{2}+(A_{y})^{2})}}$

और कोण इस प्रकार ज्ञात किया जा सकता है:

$\phi =tan^{-1}(Ay/Ax)$

इसलिए, हम यह निष्कर्ष निकाल सकते हैं कि:

यदि किसी सदिश के अवयव दिए गए हैं, तो हम परिणामी सदिश निर्धारित कर सकते हैं
इसी तरह, यदि सदिश प्रदान किया गया है, तो हम उपरोक्त समीकरणों का उपयोग करके सदिश के अवयवों को निर्धारित कर सकते हैं

इसी तरह, यदि ये सदिश क्रमित युग्मों यानी स्तंभ सदिशों में व्यक्त किए गए हैं, तो हम उनके अवयवों का उपयोग करके सदिशों पर योगफल कर सकते हैं। उदाहरण के लिए, दो सदिश $P$ और $Q$ पर विचार करें।

$P=(p_{1},p_{2})$

$Q=(q_{1},q_{2})$

परिणामी सदिश $M$ को दो सदिशों $P$ और $Q$ पर सदिश योगफल करके, इन दोनों सदिशों के क्रमशः $x$ और $y$ अवयवों को जोड़कर प्राप्त किया जा सकता है।

M = P + Q

$M=(p_{1}+q_{1},p_{2}+q_{2})$

इसे स्पष्ट रूप से इस प्रकार व्यक्त किया जा सकता है:

$M_{x}=p_{1}+q_{1}$

$M_{y}=p_{2}+q_{2}$

परिणामी सदिश $M$ का परिमाण ज्ञात करने का परिमाण सूत्र है: $|M|={\sqrt {((M_{x})^{2}+(M_{y})^{2})}}$

और कोण की गणना $\phi =tan^{-1}(M_{y}/M_{x})$ के रूप में की जा सकती है

महत्वपूर्ण टिप्पणियाँ

यहाँ कुछ बिंदुओं की सूची दी गई है जिन्हें सदिशों के योगफल का अध्ययन करते समय याद रखना चाहिए:

सदिशों को दिशा और परिमाण के संयोजन के रूप में दर्शाया जाता है और उन्हेंबाण चिन्ह के निरूपण से खींचा जाता है।
यदि किसी सदिश के अवयव दिए गए हैं, तो हम परिणामी सदिश निर्धारित कर सकते हैं।
सदिशों के योगफल के लिए प्रसिद्ध त्रिभुज नियम का उपयोग किया जा सकता है और इस विधि को हेड-टू-टेल विधि भी कहा जाता है।

@@ Line 1: / Line 1: @@
-Addition of Vectors
+सदिशों का योगफल का अनुप्रयोग भौतिक राशियों में होता है जहाँ सदिश का उपयोग वेग, विस्थापन और त्वरण को दर्शाने के लिए किया जाता है।
-[[Category:बीजगणित]]
+* सदिशों को ज्यामितीय रूप से जोड़ना उनकी अन्त्य बिंदुओं  को एक साथ रखना है और इस प्रकार एक समांतर चतुर्भुज का निर्माण करना है। सदिशों  का योग समांतर चतुर्भुज का विकर्ण होता है जो अन्त्य के प्रतिच्छेदन से प्रारंभ होता है।
-[[Category:सदिश बीजगणित]]
+* बीजगणितीय रूप से सदिशों को जोड़ना उनके संगत अवयवों को जोड़ना है।
+इस लेख में, आइए हल किए गए उदाहरणों के साथ सदिशों  के योग, उनके गुणों और विभिन्न नियमों के बारे में जानें।
+== परिभाषा ==
+[[सदिश]] को दिशा और परिमाण के संयोजन के रूप में दर्शाया जाता है और उन्हें एक वर्णमाला और उनके ऊपर एक बाण चिन्ह (या) बोल्ड में लिखे गए वर्णमाला के साथ लिखा जाता है। दो सदिशों, <math>a</math> और <math>b,</math> को सदिश जोड़ का उपयोग करके एक साथ जोड़ा जा सकता है, और परिणामी सदिश को इस प्रकार लिखा जा सकता है: <math>a + b</math>। सदिश जोड़ के गुणों के बारे में जानने से पहले, हमें उन शर्तों के बारे में जानना होगा जिनका सदिश जोड़ते समय पालन किया जाना चाहिए।
+शर्तें इस प्रकार हैं:
+* [[सदिशों के प्रकार|सदिशों]] को तभी जोड़ा जा सकता है जब वे एक ही स्वरूप के हों। उदाहरण के लिए, त्वरण को केवल त्वरण के साथ जोड़ा जाना चाहिए, द्रव्यमान के साथ नहीं
+* हम सदिशों और अदिशों को एक साथ नहीं जोड़ सकते
+दो सदिशों  <math>C</math> और <math>D </math> पर विचार करें, जहाँ, '''C''' <math>= C_xi + C_yj + C_zk</math>  और '''D''' <math>= D_xi + D_yj + D_zk</math> ।  फिर, परिणामी सदिश (या सदिश योग सूत्र) '''R = C + D''' <math>= (C_x + D_x)i + (C_y + D_y)j + (C_z + C_z) k</math> है
+== सदिशों का योगफल के गुण ==
+सदिश जोड़ बीजीय जोड़ से अलग है। सदिश जोड़ करते समय विचार किए जाने वाले कुछ महत्वपूर्ण गुण यहां दिए गए हैं:
+{| class="wikitable"
+|+
+!सदिशों का योगफल के गुण
+!स्पष्टीकरण
+|-
+!तत्समक का अस्तित्व
+|किसी भी सदिश '''v''' के लिए ,
+'''v''' + '''0''' = '''v'''
+यहाँ, '''0'''  सदिश योगात्मक पहचान है।
+|-
+!व्युत्क्रम का अस्तित्व
+|किसी भी सदिश '''v''' के लिए ,
+'''v''' + - '''v''' = '''0'''
+और इस प्रकार प्रत्येक सदिश के लिए एक योज्य व्युत्क्रम उपस्थित होता है।
+|-
+!क्रम विनिमेयता
+|योग क्रमविनिमेय है; किसी भी दो स्वेच्छ सदिश '''c''',और '''d''', के लिए,
+'''c''' + '''d''' = '''d''' + '''c'''
+|-
+!साहचर्यता
+|योग क्रमविनिमेय है; किसी भी तीन स्वेच्छ सदिश '''i,j''' और '''k''' के लिए
+'''i''' + '''j''' + '''k''' = '''i''' + '''j''' + '''k'''
+अर्थात, जोड़ने का क्रम मायने नहीं रखता
+|}
+== सदिशों का आलेखीय रूप से योगफल ==
+सदिशों  का योगफल ग्राफिकल और गणितीय विधियों का उपयोग करके किया जा सकता है। ये विधियाँ इस प्रकार हैं:
+* अवयवों का उपयोग करके सदिश योगफल
+* सदिशों  के योगफल का [[सदिश योग का त्रिभुज नियम|त्रिभुज नियम]]
+* सदिशों  के योगफल का समांतर [[सदिश योग का समांतर चतुर्भुज नियम|चतुर्भुज नियम]]
+[[File:सदिशों का योगफल.jpg|thumb|262x262px|सदिशों का योगफल]]
+== अवयवों का उपयोग करके सदिशों का योगफल ==
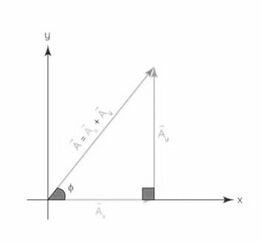
+कार्टेशियन निर्देशांक में दर्शाए गए सदिश को ऊर्ध्वाधर और क्षैतिज अवयवों में विघटित किया जा सकता है। उदाहरण के लिए, नीचे दी गई छवि में दिखाए गए कोण <math>\phi</math> पर एक सदिश <math>A</math> को इसके ऊर्ध्वाधर और क्षैतिज अवयवों में विघटित किया जा सकता है:
+उपरोक्त छवि में,
+'''Ax,'''  क्षैतिज अक्ष (<math>x</math>-अक्ष) के साथ सदिश <math>A</math> के अवयव को दर्शाता है, और
+'''Ay,'''  ऊर्ध्वाधर अक्ष (<math>y</math>-अक्ष) के साथ सदिश <math>A</math> के अवयव को दर्शाता है।
+हम देख सकते हैं कि तीनों सदिश एक समकोण त्रिभुज बनाते हैं और सदिश <math>A</math> को इस प्रकार व्यक्त किया जा सकता है:
+'''A''' = '''Ax''' + '''Ay'''
+गणितीय रूप से, दिए गए सदिश के परिमाण और कोण का उपयोग करके, हम सदिश के अवयवों को निर्धारित कर सकते हैं।
+'''Ax'''  <math>= A\  cos \phi</math>
+'''Ay''' <math>= A\  sin \phi</math>
+दो सदिशों के लिए, यदि उनके क्षैतिज और ऊर्ध्वाधर अवयव दिए गए हैं, तो परिणामी सदिश की गणना की जा सकती है। उदाहरण के लिए, यदि '''Ax''' और '''Ay''' के मान दिए गए हैं, तो हम सदिश <math>A</math> के कोण और परिमाण की गणना इस प्रकार कर पाएंगे:
+<math>|A| = \sqrt{((A_x)^2+(A_y)^2)}</math>
+और कोण इस प्रकार ज्ञात किया जा सकता है:
+<math>\phi = tan^{-1} (Ay/ Ax)</math>
+इसलिए, हम यह निष्कर्ष निकाल सकते हैं कि:
+* यदि किसी सदिश के अवयव दिए गए हैं, तो हम परिणामी सदिश निर्धारित कर सकते हैं
+* इसी तरह, यदि सदिश प्रदान किया गया है, तो हम उपरोक्त समीकरणों का उपयोग करके सदिश के अवयवों को निर्धारित कर सकते हैं
+इसी तरह, यदि ये सदिश क्रमित युग्मों यानी स्तंभ सदिशों में व्यक्त किए गए हैं, तो हम उनके अवयवों का उपयोग करके सदिशों पर योगफल कर सकते हैं। उदाहरण के लिए, दो सदिश <math>P</math> और <math>Q</math> पर विचार करें।
+<math>P = (p_1, p_2)</math>
+<math>Q = (q_1, q_2)</math>
+परिणामी सदिश <math>M</math> को दो सदिशों  <math>P</math> और <math>Q</math> पर सदिश योगफल करके, इन दोनों सदिशों के क्रमशः  <math>x</math> और <math>y</math> अवयवों को जोड़कर प्राप्त किया जा सकता है।
+'''M =''' '''P +''' '''Q'''
+<math>M = (p_1+q_1, p_2+ q_2)</math>
+इसे स्पष्ट रूप से इस प्रकार व्यक्त किया जा सकता है:
+<math>M_x = p_1 + q_1</math>
+<math>M_y = p_2 + q_2</math>
+परिणामी सदिश <math>M</math> का परिमाण ज्ञात करने का परिमाण सूत्र है:  <math>|M| = \sqrt{((M_x)^2+(M_y)^2)}</math>
+और कोण की गणना  <math>\phi = tan^{-1}(M_y/ M_x)</math> के रूप में की जा सकती है
+==महत्वपूर्ण  टिप्पणियाँ==
+यहाँ कुछ बिंदुओं की सूची दी गई है जिन्हें सदिशों  के योगफल का अध्ययन करते समय याद रखना चाहिए:
+* सदिशों  को दिशा और परिमाण के संयोजन के रूप में दर्शाया जाता है और उन्हेंबाण चिन्ह  के निरूपण से खींचा जाता है।
+* यदि किसी सदिश के अवयव दिए गए हैं, तो हम परिणामी सदिश निर्धारित कर सकते हैं।
+* सदिशों के योगफल के लिए प्रसिद्ध त्रिभुज नियम का उपयोग किया जा सकता है और इस विधि को हेड-टू-टेल विधि भी कहा जाता है।
+[[Category:सदिश बीजगणित]][[Category:गणित]][[Category:कक्षा-12]]