कोज्या के नियम: Difference between revisions
Listen
No edit summary Tag: Manual revert |
|||
| (15 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
Law of cosine | Law of cosine | ||
कोज्या (कोसाइन) का एक गणितीय सूत्र है जिसका उपयोग भुजाओं की लंबाई और एक सामान्य त्रिभुज के कोणों के बीच के संबंध को निर्धारित करने के लिए किया जाता है। यह पाइथागोरस प्रमेय का विस्तार है, जो केवल समकोण त्रिभुजों पर लागू होता है। कोज्या का नियम | कोज्या (कोसाइन) का एक गणितीय सूत्र है, जिसका उपयोग भुजाओं की लंबाई और एक सामान्य त्रिभुज के कोणों के बीच के संबंध को निर्धारित करने के लिए किया जाता है। यह पाइथागोरस प्रमेय का विस्तार है, जो केवल समकोण त्रिभुजों पर लागू होता है। कोज्या का नियम ,उन त्रिभुजों को हल करने की अनुमति देता है जो समकोण नहीं हैं। | ||
== त्रिकोणमिति में मूलभूत संबंध == | |||
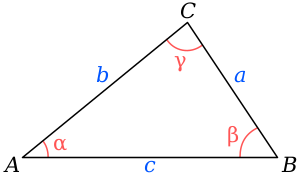
[[File:Triangle with notations 2.svg|thumb|भुजाओं और कोणों के संकेतन सहित त्रिभुज.]] | |||
एक त्रिभुज ABC की कल्पना में , जहाँ a, b, और c भुजाओं की लंबाई दर्शाते हैं, और A, B, और C संगत कोण दर्शाते हैं और जो त्रिभुजों की भुजाओं की लंबाई और कोणों को जोड़ते हैं। वे तिरछे त्रिभुजों से निपटने के दौरान भौतिकी में विशेष रूप से उपयोगी होते हैं, जहां सभी कोण समकोण नहीं होते हैं। | |||
== गणितीय रूप में == | |||
<math>c^2 = a^2+b^2- 2ab * cos(C)</math> | <math>c^2 = a^2+b^2- 2ab * cos(C)</math> | ||
| Line 15: | Line 18: | ||
"<math>C</math>" पक्ष सी के विपरीत कोण का प्रतिनिधित्व करता है। | "<math>C</math>" पक्ष सी के विपरीत कोण का प्रतिनिधित्व करता है। | ||
अनिवार्य रूप से | == अनिवार्य रूप से == | ||
कोज्या का नियम, त्रिभुज की एक भुजा की लंबाई ज्ञात करने का एक तरीका प्रदान करता है । यदि अन्य दो भुजाओं की लंबाई और उस भुजा के विपरीत कोण का माप ज्ञात हो तो उस तीसरी भुजा की लंबाई ज्ञात की जा सकती है । | |||
कोणों को हल करने के लिए सूत्र को पुनर्व्यवस्थित भी किया जा सकता है: | कोणों को हल करने के लिए सूत्र को पुनर्व्यवस्थित भी किया जा सकता है: | ||
| Line 21: | Line 25: | ||
<math>cos(C) = (a^2+b^2 - c^2) / (2ab)</math> | <math>cos(C) = (a^2+b^2 - c^2) / (2ab)</math> | ||
इसी प्रकार, | इसी प्रकार, कोज्या के नियम का उपयोग करके त्रिभुज के अन्य कोणों का हल प्राप्त कीया जा सकता है । | ||
कोज्या का नियम मार्गदर्शन(नेविगेशन), त्रिकोणमिति, भौतिकी और इंजीनियरिंग जैसे विभिन्न अनुप्रयोगों में उपयोगी है। यह | == नियम की कल्पना == | ||
[[Category:समतल में गति]] | कोज्या फलन (कोसाइन फ़ंक्शन) को इस माप के रूप में सोचें कि दो पक्ष एक-दूसरे के सापेक्ष कैसे "फैले हुए" हैं। जब उनके बीच का कोण तीव्र (90 डिग्री से कम) होता है, तो कोसाइन मान सकारात्मक होता है, और समीकरण में घटाव शब्द समझ में आता है। कोण जितना चौड़ा होगा, कोसाइन मान उतना ही 0 के करीब होगा, प्रभावी रूप से "दंड" शब्द कम हो जाएगा और पक्ष की लंबाई (ए) कम हो जाएगी। | ||
== नियम के अनुप्रयोग == | |||
कोज्या का नियम मार्गदर्शन(नेविगेशन), त्रिकोणमिति, भौतिकी और इंजीनियरिंग जैसे विभिन्न अनुप्रयोगों में उपयोगी है। यह नियम किसी भी आकृति और आकार के त्रिभुजों का विश्लेषण करने और उन्हें हल करने की अनुमति देता है, न कि केवल समकोण त्रिभुजों को। | |||
=== भौतिकी में अनुप्रयोग === | |||
कोसाइन के नियमों का भौतिकी में, विशेषकर यांत्रिकी और विद्युत चुंबकत्व में, कई अनुप्रयोग हैं। यहां कुछ उदाहरण दिए गए हैं: | |||
===== प्रक्षेप्य गति ===== | |||
एक कोण पर प्रक्षेपित प्रक्षेप्य के प्रक्षेप पथ की गणना करना। | |||
===== संतुलन में बल ===== | |||
स्थिर संतुलन में किसी वस्तु पर कार्य करने वाले बलों का विश्लेषण करना। | |||
===== विवर्तन ===== | |||
विवर्तन पैटर्न में फ्रिजों के अंतर को समझना। | |||
===== क्रिस्टल संरचनाएँ ===== | |||
क्रिस्टल जाली में परमाणुओं के बीच के कोण का निर्धारण। | |||
== संक्षेप में == | |||
त्रिकोणमिति में मूलभूत संबंध में, एक त्रिभुज ABC की कल्पना करने पर , जहाँ a, b, और c भुजाओं की लंबाई दर्शा रही हो , और A, B, और C संगत कोण दर्शाते हों और जो त्रिभुजों की भुजाओं की लंबाई और कोणों को जोड़ते हों ये नियम उपयोगी हैं। ये नियम तिरछे त्रिभुजों के भुजाओं व कोणों की भौतिकी में विशेष रूप से उपयोगी होते हैं, जहां सभी कोण समकोण नहीं होते हैं। | |||
[[Category:समतल में गति]][[Category:भौतिक विज्ञान]][[Category:कक्षा-11]] | |||
Latest revision as of 10:23, 21 January 2024
Law of cosine
कोज्या (कोसाइन) का एक गणितीय सूत्र है, जिसका उपयोग भुजाओं की लंबाई और एक सामान्य त्रिभुज के कोणों के बीच के संबंध को निर्धारित करने के लिए किया जाता है। यह पाइथागोरस प्रमेय का विस्तार है, जो केवल समकोण त्रिभुजों पर लागू होता है। कोज्या का नियम ,उन त्रिभुजों को हल करने की अनुमति देता है जो समकोण नहीं हैं।
त्रिकोणमिति में मूलभूत संबंध
एक त्रिभुज ABC की कल्पना में , जहाँ a, b, और c भुजाओं की लंबाई दर्शाते हैं, और A, B, और C संगत कोण दर्शाते हैं और जो त्रिभुजों की भुजाओं की लंबाई और कोणों को जोड़ते हैं। वे तिरछे त्रिभुजों से निपटने के दौरान भौतिकी में विशेष रूप से उपयोगी होते हैं, जहां सभी कोण समकोण नहीं होते हैं।
गणितीय रूप में
इस समीकरण में:
"" कोण सी के विपरीत पक्ष की लंबाई का प्रतिनिधित्व करता है।
"" और "" त्रिकोण के अन्य दो पक्षों की लंबाई का प्रतिनिधित्व करते हैं।
"" पक्ष सी के विपरीत कोण का प्रतिनिधित्व करता है।
अनिवार्य रूप से
कोज्या का नियम, त्रिभुज की एक भुजा की लंबाई ज्ञात करने का एक तरीका प्रदान करता है । यदि अन्य दो भुजाओं की लंबाई और उस भुजा के विपरीत कोण का माप ज्ञात हो तो उस तीसरी भुजा की लंबाई ज्ञात की जा सकती है ।
कोणों को हल करने के लिए सूत्र को पुनर्व्यवस्थित भी किया जा सकता है:
इसी प्रकार, कोज्या के नियम का उपयोग करके त्रिभुज के अन्य कोणों का हल प्राप्त कीया जा सकता है ।
नियम की कल्पना
कोज्या फलन (कोसाइन फ़ंक्शन) को इस माप के रूप में सोचें कि दो पक्ष एक-दूसरे के सापेक्ष कैसे "फैले हुए" हैं। जब उनके बीच का कोण तीव्र (90 डिग्री से कम) होता है, तो कोसाइन मान सकारात्मक होता है, और समीकरण में घटाव शब्द समझ में आता है। कोण जितना चौड़ा होगा, कोसाइन मान उतना ही 0 के करीब होगा, प्रभावी रूप से "दंड" शब्द कम हो जाएगा और पक्ष की लंबाई (ए) कम हो जाएगी।
नियम के अनुप्रयोग
कोज्या का नियम मार्गदर्शन(नेविगेशन), त्रिकोणमिति, भौतिकी और इंजीनियरिंग जैसे विभिन्न अनुप्रयोगों में उपयोगी है। यह नियम किसी भी आकृति और आकार के त्रिभुजों का विश्लेषण करने और उन्हें हल करने की अनुमति देता है, न कि केवल समकोण त्रिभुजों को।
भौतिकी में अनुप्रयोग
कोसाइन के नियमों का भौतिकी में, विशेषकर यांत्रिकी और विद्युत चुंबकत्व में, कई अनुप्रयोग हैं। यहां कुछ उदाहरण दिए गए हैं:
प्रक्षेप्य गति
एक कोण पर प्रक्षेपित प्रक्षेप्य के प्रक्षेप पथ की गणना करना।
संतुलन में बल
स्थिर संतुलन में किसी वस्तु पर कार्य करने वाले बलों का विश्लेषण करना।
विवर्तन
विवर्तन पैटर्न में फ्रिजों के अंतर को समझना।
क्रिस्टल संरचनाएँ
क्रिस्टल जाली में परमाणुओं के बीच के कोण का निर्धारण।
संक्षेप में
त्रिकोणमिति में मूलभूत संबंध में, एक त्रिभुज ABC की कल्पना करने पर , जहाँ a, b, और c भुजाओं की लंबाई दर्शा रही हो , और A, B, और C संगत कोण दर्शाते हों और जो त्रिभुजों की भुजाओं की लंबाई और कोणों को जोड़ते हों ये नियम उपयोगी हैं। ये नियम तिरछे त्रिभुजों के भुजाओं व कोणों की भौतिकी में विशेष रूप से उपयोगी होते हैं, जहां सभी कोण समकोण नहीं होते हैं।