निर्देशांक ज्यामिति: Difference between revisions

Latest revision as of 08:58, 5 November 2024

इस ग्रह पर प्रत्येक स्थान के निर्देशांक हैं जो हमें इसे विश्व मानचित्र पर आसानी से ढूंढने में सहायता करते हैं। हमारी पृथ्वी की समन्वय प्रणाली काल्पनिक रेखाओं से बनी है जिन्हें अक्षांश और देशांतर कहा जाता है। शून्य घात 'ग्रीनविच देशांतर' और शून्य घात 'भूमध्य रेखा अक्षांश' इस समन्वय प्रणाली की प्रारंभिक रेखाएँ हैं। इसी प्रकार एक समतल या कागज के टुकड़े पर बिंदु का पता लगाने पर, हमें क्षैतिज $X$ -अक्ष और ऊर्ध्वाधर $Y$ -अक्ष के साथ समन्वय अक्ष प्राप्त होते हैं।

परिभाषा

निर्देशांक ज्यामिति, ज्यामितीय आकृतियों को निर्देशांक अक्षों में आलेखित करके उनका अध्ययन है। सीधी रेखाओं, वक्रों, वृत्तों, दीर्घवृत्त, अतिपरवलय और बहुभुज जैसी आकृतियों को आसानी से खींचा जा सकता है और समन्वय अक्षों में पैमाने पर प्रस्तुत किया जा सकता है। इसके अलावा, समन्वय ज्यामिति बीजगणितीय रूप से काम करने और समन्वय प्रणाली की सहायता से ज्यामितीय आंकड़ों के गुणों का अध्ययन करने में सहायता करती है।

निर्देशांक ज्यामिति क्या है?

निर्देशांक ज्यामिति गणित की एक महत्वपूर्ण शाखा है, जो ज्यामितीय आकृतियों को द्वि-आयामी तल में प्रस्तुत करने और इन आकृतियों के गुणों को जानने में सहायता करती है।

निर्देशांक तल

कार्टेशियन तल समतल स्थान को दो आयामों में विभाजित करता है और बिंदुओं को आसानी से ज्ञात करने के लिए उपयोगी होता है। इसे निर्देशांक तल भी कहा जाता है। निर्देशांक तल के दो अक्ष क्षैतिज $X$ -अक्ष और ऊर्ध्वाधर $Y$ -अक्ष हैं। ये निर्देशांक अक्ष समतल को चार चतुर्भुजों में विभाजित करते हैं, और इन अक्षों का प्रतिच्छेद बिंदु मूल $(0,0)$ है। इसके अलावा, निर्देशांक तल में किसी भी बिंदु को एक बिंदु $(x,y)$ द्वारा संदर्भित किया जाता है, जहां $x$ मान के संदर्भ में बिंदु की स्थिति है $X$ -अक्ष और $y$ मान $Y$ -अक्ष के संदर्भ में बिंदु की स्थिति है।

निर्देशांक तल के चार चतुर्थांशों (चित्र 1) में दर्शाए गए बिंदु के गुण हैं:

मूल बिंदु $O$ , $X$ -अक्ष और $Y$ -अक्ष का प्रतिच्छेदन बिंदु है और इसके निर्देशांक $(0,0)$ हैं।
मूल बिंदु $O$ के दाईं ओर $X$ -अक्ष धनात्मक $X$ -अक्ष है और मूल बिंदु $O$ के बाईं ओर ऋणात्मक $X$ -अक्ष है। साथ ही, मूल बिंदु $O$ के ऊपर $Y$ -अक्ष धनात्मक $Y$ -अक्ष है, और मूल बिंदु $O$ के नीचे ऋणात्मक $Y$ -अक्ष है।
प्रथम चतुर्थांश $(x,y)$ में दर्शाए गए बिंदु के दोनों मान धनात्मक हैं और इसे धनात्मक $X$ -अक्ष और धनात्मक $Y$ -अक्ष के संदर्भ में आलेखित किया गया है।
दूसरे चतुर्थांश में दर्शाया गया बिंदु $(-x,y)$ है और इसे ऋणात्मक $X$ -अक्ष और धनात्मक के संदर्भ में आलेखित किया गया है

$Y$ -अक्ष ।

तीसरे चतुर्थांश $(-x,-y)$ में दर्शाए गए बिंदु को ऋणात्मक $X$ -अक्ष और ऋणात्मक $Y$ -अक्ष के संदर्भ में आलेखित किया गया है।
चौथे चतुर्थांश $(x,-y)$ में दर्शाए गए बिंदु को धनात्मक $X$ -अक्ष और ऋणात्मक $Y$ -अक्ष के संदर्भ में आलेखित किया गया है।

चित्र. 1

किसी बिंदु के निर्देशांक

निर्देशांक एक पता है, जो अंतरिक्ष में एक बिंदु का पता लगाने में मदद करता है। द्वि-आयामी अंतरिक्ष के लिए, एक बिंदु के निर्देशांक $(x,y)$ हैं। यहाँ हम इन दो महत्वपूर्ण शब्दों पर ध्यान देते हैं।

भुज: यह बिंदु $(x,y)$ में $x$ का मान है, तथा मूल बिंदु से $X$ -अक्ष के अनुदिश इस बिंदु की दूरी है
कोटि: यह बिंदु $(x,y)$ में $y$ मान है, और $X$ -अक्ष से बिंदु की लंबवत दूरी है, जो $Y$ -अक्ष के समानांतर है।

किसी बिंदु के निर्देशांक दूरी, मध्यबिंदु, रेखा का ढलान, रेखा का समीकरण आदि ज्ञात करने के लिए उपयोगी होते हैं।

@@ Line 1: / Line 1: @@
+इस ग्रह पर प्रत्येक स्थान के निर्देशांक हैं जो हमें इसे विश्व मानचित्र पर आसानी से ढूंढने में सहायता करते हैं। हमारी पृथ्वी की समन्वय प्रणाली काल्पनिक रेखाओं से बनी है जिन्हें अक्षांश और देशांतर कहा जाता है। शून्य घात 'ग्रीनविच देशांतर' और शून्य घात 'भूमध्य रेखा अक्षांश' इस समन्वय प्रणाली की प्रारंभिक रेखाएँ हैं। इसी प्रकार एक समतल या कागज के टुकड़े पर बिंदु का पता लगाने पर, हमें क्षैतिज <math>X</math>-अक्ष और ऊर्ध्वाधर <math>Y</math>-अक्ष के साथ समन्वय अक्ष प्राप्त होते हैं।
-[[Category:ज्यामिति]]
+== परिभाषा ==
-[[Category:निर्देशांक ज्यामिति]][[Category:कक्षा-9]]
+निर्देशांक ज्यामिति, ज्यामितीय आकृतियों को निर्देशांक अक्षों में आलेखित करके उनका अध्ययन है। सीधी रेखाओं, वक्रों, वृत्तों, दीर्घवृत्त, अतिपरवलय और बहुभुज जैसी आकृतियों को आसानी से खींचा जा सकता है और समन्वय अक्षों में पैमाने पर प्रस्तुत किया जा सकता है। इसके अलावा, समन्वय ज्यामिति बीजगणितीय रूप से काम करने और समन्वय प्रणाली की सहायता से ज्यामितीय आंकड़ों के गुणों का अध्ययन करने में सहायता करती है।
+== निर्देशांक ज्यामिति क्या है? ==
+निर्देशांक ज्यामिति गणित की एक महत्वपूर्ण शाखा है, जो ज्यामितीय आकृतियों को द्वि-आयामी तल में प्रस्तुत करने और इन आकृतियों के गुणों को जानने में सहायता करती है।
+=== निर्देशांक तल ===
+[[कार्टेशियन पद्धति|कार्टेशियन]] तल समतल स्थान को दो आयामों में विभाजित करता है और बिंदुओं को आसानी से ज्ञात करने के लिए उपयोगी होता है। इसे निर्देशांक तल भी कहा जाता है। निर्देशांक तल के दो अक्ष क्षैतिज <math>X</math>-अक्ष और ऊर्ध्वाधर <math>Y</math>-अक्ष हैं। ये निर्देशांक अक्ष समतल को चार चतुर्भुजों में विभाजित करते हैं, और इन अक्षों का प्रतिच्छेद बिंदु मूल <math>(0,0)</math> है। इसके अलावा, निर्देशांक तल में किसी भी बिंदु को एक बिंदु <math>(x,y)</math> द्वारा संदर्भित किया जाता है, जहां <math>x</math> मान के संदर्भ में बिंदु की स्थिति है <math>X</math>-अक्ष और <math>y</math> मान <math>Y</math>-अक्ष के संदर्भ में बिंदु की स्थिति है।
+[[निर्देशांक तल]] के चार चतुर्थांशों (चित्र 1) में दर्शाए गए बिंदु के गुण हैं:
+* मूल बिंदु <math>O</math>, <math>X</math>-अक्ष और <math>Y</math>-अक्ष का प्रतिच्छेदन बिंदु है और इसके निर्देशांक <math>(0,0)</math> हैं।
+* मूल बिंदु <math>O</math> के दाईं ओर <math>X</math>-अक्ष धनात्मक <math>X</math>-अक्ष है और मूल बिंदु <math>O</math> के बाईं ओर ऋणात्मक <math>X</math>-अक्ष है। साथ ही, मूल बिंदु <math>O</math> के ऊपर <math>Y</math>-अक्ष धनात्मक <math>Y</math>-अक्ष है, और मूल बिंदु <math>O</math> के नीचे ऋणात्मक <math>Y</math>-अक्ष है।
+* प्रथम चतुर्थांश <math>(x,y)</math> में दर्शाए गए बिंदु के दोनों मान धनात्मक हैं और इसे धनात्मक <math>X</math>-अक्ष और धनात्मक <math>Y</math>-अक्ष के संदर्भ में आलेखित किया गया है।
+* दूसरे चतुर्थांश में दर्शाया गया बिंदु <math>(-x,y)</math> है और इसे ऋणात्मक <math>X</math>-अक्ष और धनात्मक के संदर्भ में आलेखित किया गया है
+<math>Y</math>-अक्ष ।
+* तीसरे चतुर्थांश <math>(-x,-y)</math> में दर्शाए गए बिंदु को ऋणात्मक <math>X</math>-अक्ष और ऋणात्मक <math>Y</math>-अक्ष के संदर्भ में आलेखित किया गया है।
+* चौथे चतुर्थांश <math>(x,-y)</math> में दर्शाए गए बिंदु को धनात्मक <math>X</math>-अक्ष और ऋणात्मक <math>Y</math>-अक्ष के संदर्भ में आलेखित किया गया है।
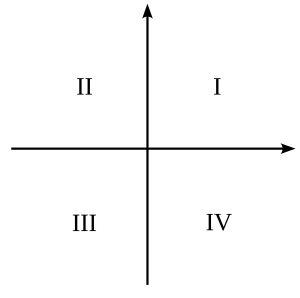
+[[File:Cartesian-coordinate-system-with-quadrant.svg|alt=Fig. 1|none|thumb|चित्र. 1]]
+=== किसी बिंदु के निर्देशांक ===
+निर्देशांक एक पता है, जो अंतरिक्ष में एक बिंदु का पता लगाने में मदद करता है। द्वि-आयामी अंतरिक्ष के लिए, एक बिंदु के निर्देशांक <math>(x,y)</math> हैं। यहाँ हम इन दो महत्वपूर्ण शब्दों पर ध्यान देते हैं।
+* '''भुज:''' यह बिंदु <math>(x,y)</math> में <math>x</math> का मान है, तथा मूल बिंदु से <math>X</math>-अक्ष के अनुदिश इस बिंदु की दूरी है
+* '''कोटि:''' यह बिंदु <math>(x,y)</math> में <math>y</math> मान है, और <math>X</math>-अक्ष से बिंदु की लंबवत दूरी है, जो <math>Y</math>-अक्ष के समानांतर है।
+किसी बिंदु के निर्देशांक दूरी, मध्यबिंदु, रेखा का ढलान, रेखा का समीकरण आदि ज्ञात करने के लिए उपयोगी होते हैं।
+[[Category:निर्देशांक ज्यामिति]]
+[[Category:कक्षा-9]]
+[[Category:गणित]]