सम्मिश्र संख्याएँ

सम्मिश्र संख्याएँ ऋणात्मक संख्याओं का वर्गमूल ज्ञात करने में सहायक होती हैं। जटिल संख्याओं की अवधारणा का उल्लेख पहली बार पहली शताब्दी में एक यूनानी गणितज्ञ, अलेक्जेंड्रिया के हीरो द्वारा किया गया था जब उन्होंने एक ऋणात्मक संख्या का वर्गमूल ज्ञात करने का प्रयास किया था। लेकिन उन्होंने केवल नकारात्मक को सकारात्मक में बदल दिया और मात्र संख्यात्मक मूल मान लिया। इसके अलावा, एक जटिल संख्या की वास्तविक पहचान 16वीं शताब्दी में इतालवी गणितज्ञ गेरोलामो कार्डानो द्वारा घन और द्विघात बहुपद अभिव्यक्तियों की नकारात्मक जड़ों को ज्ञात करने की प्रक्रिया में परिभाषित की गई थी।

परिभाषा

सम्मिश्र संख्या एक वास्तविक संख्या और एक काल्पनिक संख्या का योग है। एक सम्मिश्र संख्या $a+ib$ के रूप की होती है और प्रायः इसे $z$ द्वारा दर्शाया जाता है।, $z=a+ib$

यहाँ $a$, $b$ दोनों वास्तविक संख्याएँ हैं और $i={\sqrt {-1}}$ । मान '$a$' को वास्तविक भाग कहा जाता है जिसे $Re\ z$,द्वारा दर्शाया जाता है और '$b$' काल्पनिक भाग कहलाता है $Im\ z$ द्वारा दर्शाया जाता है। साथ ही $ib$ को एक काल्पनिक संख्या भी कहा जाता है।

सम्मिश्र संख्याओं के उदाहरण:

$z=2+i3$

$z=-1+i{\sqrt {3}}$

$z=4+i\left[{\frac {-1}{11}}\right]$

चित्र-1 सम्मिश्र संख्याएँ

सम्मिश्र संख्या का निरूपण

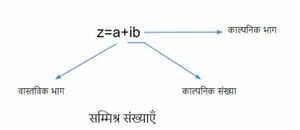
सम्मिश्र संख्या को निरूपित करने की विधि को चित्र-1 में दिखाया गया है।

उदाहरण के लिए: $z=2+i5$ , तब

वास्तविक भाग: $Re\ z=2$

काल्पनिक भाग: $Im\ z=5$

सम्मिश्र संख्याओं की समानता

दो सम्मिश्र संख्याएँ $z_{1}=a+ib$ और $z_{2}=c+id$ समान होंगी यदि $a=c$ और $b=d$

उदाहरण: यदि $5x+i(4x-y)=4+i(-5)$ जहाँ x और y वास्तविक संख्याएँ हैं, तो x और y का मान ज्ञात कीजिए।

$5x+i(4x-y)=4+i(-5)................(1)$

$(1)$ के वास्तविक और काल्पनिक भागों को समीकृत करने पर हमें प्राप्त होता है

$5x=4$ अत: $x={\frac {4}{5}}$

$4x-y=-5$

$4\left[{\frac {4}{5}}\right]-y=-5$

$y=4\left[{\frac {4}{5}}\right]+5$

$y={\frac {16+25}{5}}={\frac {41}{5}}$

उत्तर: $x={\frac {4}{5}}$ और $y={\frac {41}{5}}$