वर्धमान और ह्रासमान फलन: Difference between revisions

Latest revision as of 14:39, 3 December 2024

वर्धमान और ह्रासमान फलन कलन में ऐसे फलन हैं जिनके लिए $x$ के मान में वृद्धि के साथ $f(x)$ का मान क्रमशः वर्धमान और ह्रासमान है। वर्धमान और ह्रासमान फलनों के व्यवहार की जाँच करने के लिए फलन $f(x)$ के अवकलज का उपयोग किया जाता है। यदि $x$ के मान में वृद्धि के साथ $f(x)$ का मान वर्धमान है तो फलन को वर्धमान हुआ कहा जाता है और यदि $x$ के मान में वृद्धि के साथ $f(x)$ का मान ह्रासमान है तो फलन को ह्रासमान हुआ कहा जाता है।

इस लेख में, हम वर्धमान और ह्रासमान फलनों की अवधारणा, उनके गुणों, ग्राफ़िकल निरूपण और बेहतर समझ के लिए उदाहरणों के साथ वर्धमान और ह्रासमान फलनों के परीक्षण के लिए प्रमेयों का अध्ययन करेंगे।

परिभाषा

वर्धमान और ह्रासमान फलन वे फलन हैं जिनके आलेख क्रमशः ऊपर और नीचे जाते हैं जैसे ही हम $x$ -अक्ष के दाईं ओर वर्धमान हैं। वर्धमान और ह्रासमान फलनों को गैर-ह्रासमान और गैर-वर्धमान फलन भी कहा जाता है। आइए वर्धमान और ह्रासमान फलनों की औपचारिक परिभाषा को समझते हैं ताकि उनका अर्थ समझ सकें:

वर्धमान फलन - एक फलन $f(x)$ को अंतराल $I$ पर वर्धमान हुआ कहा जाता है यदि $I$ में किसी भी दो संख्याओं $x$ और $y$ के लिए इस तरह से $x<y,$ हमारे पास $f(x)\leq f(y)$ है।
ह्रासमान फलन - एक फलन $f(x)$ को अंतराल $I$ पर ह्रासमान हुए कहा जाता है यदि $I$ में किसी भी दो संख्याओं $x$ और $y$ के लिए इस तरह से $x<y,$ हमारे पास $f(x)\geq f(y)$ है।
निरंतर से वर्धमान फलन - एक फलन $f(x)$ को अंतराल $I$ पर निरंतर से वर्धमान हुआ कहा जाता है यदि $I$ में किसी भी दो संख्याओं $x$ और $y$ के लिए इस तरह से $x<y,$ हमारे पास $f(x)<f(y)$ है।
निरंतर से ह्रासमान फलन - एक फलन $f(x)$ को अंतराल $I$ पर निरंतर से ह्रासमान हुए कहा जाता है यदि $I$ में किसी भी दो संख्याओं $x$ और $y$ के लिए इस तरह से $x<y,$ हमारे पास $f(x)>f(y)$ है।

वर्धमान और ह्रासमान फलन

आलेखीय प्रतिनिधित्व

अब, जब हम वर्धमान और ह्रासमान फलनों का अर्थ और परिभाषा जानते हैं, तो आइए वर्धमान और ह्रासमान फलनों का आलेखीय प्रतिनिधित्व देखें जो हमें फलनों के व्यवहार को समझने में सहायता करेगा।

ऊपर दिए गए आलेख निरंतर से बढ़ते, निरंतर से घटते, वर्धमान और ह्रासमान फलन का आलेखीय प्रतिनिधित्व दिखाते हैं। जैसा कि हम ऊपर दिए गए आलेख में देख सकते हैं, वर्धमान फलन में निरंतर से वर्धमान अंतराल और ऐसे अंतराल दोनों उपस्थित हैं जहाँ फलन स्थिर है। इसी तरह, ह्रासमान फलन में ऐसे अंतराल होते हैं जहाँ फलन निरंतर से घट रहा है और जहाँ फलन स्थिर है।

जाँच करने के नियम

हम किसी फलन के अवकलज का उपयोग यह जाँचने के लिए करते हैं कि यह एक वर्धमान या ह्रासमान फलन है। मान लीजिए कि एक फलन $f(x)$ एक खुले अंतराल $I$ पर अवकलनीय है, तो हमारे पास है

यदि $I$ पर $f'(x)\geq 0$ है, तो फलन को $I$ पर एक वर्धमान फलन कहा जाता है।

यदि $I$ पर $f'(x)\leq 0$ है, तो फलन को $I$ पर एक ह्रासमान फलन कहा जाता है।

उदाहरण: आइए अवधारणा को बेहतर ढंग से समझने के लिए एक उदाहरण पर विचार करें। सभी वास्तविक संख्याओं के लिए परिभाषित $f(x)=x^{3}$ पर विचार करें। $f(x)=x^{3}$ का अवकलज $f'(x)=3x^{2}$ द्वारा दिया गया है। हम जानते हैं कि किसी संख्या का वर्ग सदैव $0$ से बड़ा या बराबर होता है, इसलिए हमारे पास सभी $x$ के लिए $f'(x)=3x^{2}\geq 0$ है। इसलिए $f(x)=x^{3}$ एक वर्धमान फलन है।

गुणधर्म

चूँकि हम जानते हैं कि किसी फलन के बढ़ने या घटने की जाँच कैसे की जाती है, तो आइए वर्धमान और ह्रासमान फलनों के बीजगणितीय गुणों को देखें:

यदि फलन $f$ और $g$ एक खुले अंतराल $I$ पर वर्धमान फलन हैं, तो फलन $f+g$ का योग भी इस अंतराल पर बढ़ रहा है।
यदि फलन $f$ और $g$ एक खुले अंतराल $I$ पर ह्रासमान फलन हैं, तो फलन $f+g$ का योग भी इस अंतराल पर घट रहा है।
यदि फलन $f$ एक खुले अंतराल $I$ पर एक वर्धमान फलन है, तो विपरीत फलन $-f$ इस अंतराल पर घट रहा है।
यदि फलन $f$ एक खुले अंतराल $I$ पर एक ह्रासमान फलन है, तो विपरीत फलन $-f$ इस अंतराल पर बढ़ रहा है।
यदि फलन $f$ एक खुले अंतराल $I$ पर एक वर्धमान फलन है, तो व्युत्क्रम फलन $1/f$ इस अंतराल पर घट रहा है।
यदि फलन $f$ एक खुले अंतराल $I$ पर एक ह्रासमान फलन है, तो व्युत्क्रम फलन $1/f$ इस अंतराल पर बढ़ रहा है।
यदि फलन $f$ और $g$ एक खुले अंतराल $I$ पर वर्धमान फलन हैं और $I$ पर $f,g\geq 0$ है, तो फलन $fg$ का गुणनफल भी इस अंतराल पर बढ़ रहा है।
यदि फलन $f$ और $g$ एक खुले अंतराल $I$ पर ह्रासमान फलन हैं और $I$ पर $f,g\geq 0$ है, तो फलन $fg$ का गुणनफल भी इस अंतराल पर घट रहा है।

महत्वपूर्ण टिप्पणियाँ

फलन के पहले अवकलज का उपयोग वर्धमान और ह्रासमान फलनों की जाँच करने के लिए किया जाता है।
वर्धमान और ह्रासमान फलनों को गैर-ह्रासमान और गैर-वर्धमान फलन भी कहा जाता है।

@@ Line 1: / Line 1: @@
-Increasing and Decreasing Functions
+वर्धमान और ह्रासमान फलन कलन में ऐसे फलन हैं जिनके लिए <math>x </math> के मान में वृद्धि के साथ <math>f(x)</math> का मान क्रमशः वर्धमान  और ह्रासमान है। वर्धमान और ह्रासमान  [[फलनों के प्राचलिक रूपों के अवकलज|फलनों]] के व्यवहार की जाँच करने के लिए फलन <math>f(x)</math> के [[अवकलज]] का उपयोग किया जाता है। यदि <math>x </math> के मान में वृद्धि के साथ <math>f(x)</math> का मान वर्धमान   है तो फलन को वर्धमान   हुआ कहा जाता है और यदि <math>x </math> के मान में वृद्धि के साथ <math>f(x)</math> का मान ह्रासमान है तो फलन को ह्रासमान हुआ कहा जाता है।
+इस लेख में, हम वर्धमान और ह्रासमान  फलनों की अवधारणा, उनके गुणों, ग्राफ़िकल निरूपण और बेहतर समझ के लिए उदाहरणों के साथ वर्धमान और ह्रासमान  फलनों के परीक्षण के लिए प्रमेयों का अध्ययन करेंगे।
+== परिभाषा ==
+वर्धमान और ह्रासमान  फलन वे फलन हैं जिनके आलेख क्रमशः ऊपर और नीचे जाते हैं जैसे ही हम <math>x </math>-अक्ष के दाईं ओर वर्धमान  हैं। वर्धमान और ह्रासमान  फलनों को गैर-ह्रासमान और गैर-वर्धमान  फलन भी कहा जाता है। आइए वर्धमान और ह्रासमान  फलनों की औपचारिक परिभाषा को समझते हैं ताकि उनका अर्थ समझ सकें:
+* '''वर्धमान फलन''' - एक फलन <math>f(x)</math> को अंतराल <math>I</math> पर वर्धमान हुआ कहा जाता है यदि <math>I</math> में किसी भी दो संख्याओं <math>x </math> और <math>y  </math> के लिए इस तरह से <math>x < y, </math> हमारे पास <math>f(x) \leq f(y) </math> है।
+* '''ह्रासमान फलन''' - एक फलन <math>f(x)</math> को अंतराल <math>I</math> पर ह्रासमान हुए कहा जाता है यदि <math>I</math> में किसी भी दो संख्याओं <math>x </math> और <math>y  </math> के लिए इस तरह से <math>x < y, </math> हमारे पास <math>f(x) \geq f(y)</math> है।
+* '''निरंतर से वर्धमान फलन''' - एक फलन <math>f(x)</math> को अंतराल <math>I</math> पर निरंतर से वर्धमान  हुआ कहा जाता है यदि <math>I</math> में किसी भी दो संख्याओं <math>x </math> और <math>y  </math> के लिए इस तरह से <math>x < y, </math> हमारे पास <math>f(x) < f(y)</math> है।
+* '''निरंतर से ह्रासमान फलन''' - एक फलन <math>f(x)</math>  को अंतराल <math>I</math> पर निरंतर से ह्रासमान हुए कहा जाता है यदि <math>I</math> में किसी भी दो संख्याओं <math>x </math> और <math>y  </math> के लिए इस तरह से <math>x < y, </math> हमारे पास <math>f(x) > f(y) </math> है।
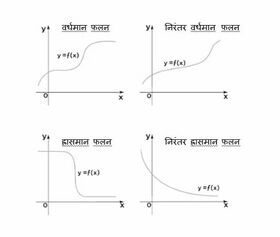
+[[File:वर्धमान और ह्रासमान फलन.jpg|thumb|280x280px|वर्धमान और ह्रासमान फलन]]
+== आलेखीय प्रतिनिधित्व ==
+अब, जब हम वर्धमान और ह्रासमान फलनों का अर्थ और परिभाषा जानते हैं, तो आइए वर्धमान और ह्रासमान फलनों  का आलेखीय प्रतिनिधित्व देखें जो हमें फलनों के व्यवहार को समझने में सहायता करेगा।
+ऊपर दिए गए आलेख निरंतर से बढ़ते, निरंतर से घटते, वर्धमान और ह्रासमान  फलन का आलेखीय प्रतिनिधित्व दिखाते हैं। जैसा कि हम ऊपर दिए गए आलेख में देख सकते हैं, वर्धमान फलन में निरंतर से वर्धमान  अंतराल और ऐसे अंतराल दोनों उपस्थित हैं जहाँ फलन स्थिर है। इसी तरह, ह्रासमान फलन में ऐसे अंतराल होते हैं जहाँ फलन निरंतर से घट रहा है और जहाँ फलन स्थिर है।
+== जाँच करने के नियम ==
+हम किसी फलन के अवकलज का उपयोग यह जाँचने के लिए करते हैं कि यह एक वर्धमान या ह्रासमान फलन है। मान लीजिए कि एक फलन <math>f(x)</math> एक खुले अंतराल <math>I</math> पर अवकलनीय है, तो हमारे पास है
+यदि <math>I</math> पर <math>f'(x) \geq 0 </math> है, तो फलन को <math>I</math> पर एक वर्धमान फलन कहा जाता है।
+यदि <math>I</math> पर <math>f'(x) \leq 0 </math> है, तो फलन को <math>I</math> पर एक ह्रासमान फलन कहा जाता है।
+उदाहरण: आइए अवधारणा को बेहतर ढंग से समझने के लिए एक उदाहरण पर विचार करें। सभी वास्तविक संख्याओं के लिए परिभाषित <math>f(x) = x^3  </math>पर विचार करें। <math>f(x) = x^3  </math> का अवकलज <math>f'(x) = 3x^2 </math> द्वारा दिया गया है। हम जानते हैं कि किसी संख्या का वर्ग सदैव <math>0  </math> से बड़ा या बराबर होता है, इसलिए हमारे पास सभी <math>x </math> के लिए <math>f'(x) = 3x^2\geq 0  </math> है। इसलिए <math>f(x) = x^3  </math> एक वर्धमान फलन है।
+== गुणधर्म ==
+चूँकि हम जानते हैं कि किसी फलन के बढ़ने या घटने की जाँच कैसे की जाती है, तो आइए वर्धमान और ह्रासमान  फलनों  के बीजगणितीय गुणों को देखें:
+* यदि फलन <math>f </math> और <math>g  </math> एक खुले अंतराल <math>I</math> पर वर्धमान  फलन हैं, तो फलन <math>f + g </math> का योग भी इस अंतराल पर बढ़ रहा है।
+* यदि फलन <math>f </math> और <math>g  </math> एक खुले अंतराल <math>I</math> पर ह्रासमान फलन हैं, तो फलन <math>f + g </math> का योग भी इस अंतराल पर घट रहा है।
+* यदि फलन <math>f </math> एक खुले अंतराल <math>I</math> पर एक वर्धमान  फलन है, तो विपरीत फलन <math>-f </math> इस अंतराल पर घट रहा है।
+* यदि फलन <math>f </math> एक खुले अंतराल <math>I</math> पर एक ह्रासमान फलन है, तो विपरीत फलन <math>-f </math> इस अंतराल पर बढ़ रहा है।
+* यदि फलन <math>f </math> एक खुले अंतराल <math>I</math> पर एक वर्धमान फलन है, तो व्युत्क्रम फलन <math>1/f </math> इस अंतराल पर घट रहा है।
+* यदि फलन <math>f </math> एक खुले अंतराल <math>I</math> पर एक ह्रासमान फलन है, तो व्युत्क्रम फलन <math>1/f </math> इस अंतराल पर बढ़ रहा है।
+* यदि फलन <math>f </math> और <math>g  </math> एक खुले अंतराल <math>I</math> पर वर्धमान  फलन हैं और <math>I</math> पर <math>f, g \geq 0 </math> है, तो फलन <math>fg </math> का गुणनफल भी इस अंतराल पर बढ़ रहा है।
+* यदि फलन <math>f </math> और <math>g  </math> एक खुले अंतराल <math>I</math> पर ह्रासमान फलन हैं और <math>I</math> पर <math>f, g \geq 0 </math> है, तो फलन <math>fg </math> का गुणनफल भी इस अंतराल पर घट रहा है।
+== महत्वपूर्ण टिप्पणियाँ ==
+* फलन के पहले अवकलज का उपयोग वर्धमान और ह्रासमान  फलनों  की जाँच करने के लिए किया जाता है।
+* वर्धमान और ह्रासमान फलनों  को गैर-ह्रासमान और गैर-वर्धमान  फलन भी कहा जाता है।
 [[Category:अवकलज के अनुप्रयोग]][[Category:गणित]][[Category:कक्षा-12]]