दो सदिशों का गुणनफल: Difference between revisions
(Updated Category) |
(images added) |
||
| (5 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
सदिशों का गुणनफल दो प्रकार का होता है। सदिश में परिमाण और दिशा दोनों होते हैं और इसके आधार पर सदिशों के दो गुणनफल होते हैं, दो सदिशों का डॉट गुणनफल और दो सदिशों का वज्र गुणनफल। दो सदिशों के डॉट गुणनफल को अदिश गुणनफल भी कहा जाता है, क्योंकि परिणामी मान एक अदिश राशि होती है। वज्र गुणनफल को [[एक अदिश से सदिश का गुणन|सदिश गुणनफल]] कहा जाता है क्योंकि परिणाम एक सदिश होता है, जो इन दो सदिशों के लंबवत होता है। | |||
आइए सदिशों के दो गुणनफल, फलन नियम, गुण, उपयोग, सदिशों के इन गुणनफलों के उदाहरणों के बारे में जानें। | |||
== परिभाषा == | |||
एक सदिश में परिमाण और दिशा दोनों होते हैं। हम दो या अधिक [[सदिशों के प्रकार|सदिशों]] को डॉट गुणनफल और वज्र गुणनफल से गुणा कर सकते हैं। आइए सदिशों के प्रत्येक गुणनफल के बारे में अधिक समझें। | |||
[[File:डॉट गुणनफल.jpg|thumb|डॉट गुणनफल]] | |||
=== डॉट गुणनफल === | |||
सदिशों के डॉट गुणनफल को सदिशों का अदिश गुणनफल भी कहा जाता है। सदिशों के डॉट गुणनफल का परिणाम एक अदिश मान होता है। सदिशों का डॉट गुणनफल दो सदिशों के परिमाणों के गुणनफल और दो सदिशों के बीच के कोण के कोसाइन के बराबर होता है। दो सदिशों के डॉट गुणनफल का परिणाम दो सदिशों के एक ही तल में होता है। डॉट गुणनफल एक सकारात्मक वास्तविक संख्या या एक नकारात्मक वास्तविक संख्या हो सकती है। | |||
मान लीजिए कि <math>a </math> और <math>b </math> दो शून्येतर सदिश हैं, और <math>\theta</math> सदिशों का सम्मिलित कोण है। तब अदिश गुणनफल या डॉट गुणनफल को <math>a\cdot b</math> द्वारा दर्शाया जाता है, जिसे इस प्रकार परिभाषित किया जाता है: | |||
<math>\overrightarrow{a }\cdot \overrightarrow{b } = |\overrightarrow{a }||\overrightarrow{b }| cos \theta</math> | |||
यहाँ, <math>\left\vert \overrightarrow{a} \right\vert, \overrightarrow{a }</math> का परिमाण है, <math>\left\vert \overrightarrow{b } \right\vert, \overrightarrow{b }</math> का परिमाण है, तथा <math>\theta</math> उनके बीच का कोण है। | |||
[[File:वज्र गुणनफल.jpg|thumb|वज्र गुणनफल]] | |||
=== वज्र गुणनफल === | |||
वज्र गुणनफल को सदिश गुणनफल भी कहा जाता है। वज्र गुणनफल सदिश गुणन का एक रूप है, जो अलग-अलग प्रकृति या प्रकार के दो सदिश के बीच किया जाता है। जब दो सदिश को एक दूसरे से गुणा किया जाता है और गुणनफल भी एक सदिश मात्रा होती है, तो परिणामी सदिश को दो सदिश का वज्र गुणनफल या सदिश गुणनफल कहा जाता है। परिणामी सदिश दो दिए गए सदिश वाले समतल के लंबवत होता है। | |||
हम इसे एक उदाहरण से समझ सकते हैं कि यदि हमारे पास <math>X-Y</math> समतल में स्थित दो सदिश हैं, तो उनका वज्र गुणनफल <math>Z</math>-अक्ष की दिशा में एक परिणामी सदिश देगा, जो <math>XY</math> समतल के लंबवत है। मूल सदिशों के बीच <math>\times</math> चिह्न का उपयोग किया जाता है। दो सदिशों का सदिश गुणनफल या वज्र गुणनफल इस प्रकार दिखाया जाता है: | |||
<math>\overrightarrow{a} \times \overrightarrow{b}=\overrightarrow{c }</math> | |||
यहाँ <math>\overrightarrow{a}</math> और <math>\overrightarrow{b}</math> दो सदिश हैं, और <math>\overrightarrow{c}</math>परिणामी सदिश है। मान लें कि <math>\theta</math>, <math>\overrightarrow{a}</math> और <math>\overrightarrow{b}</math> के बीच बना कोण है और <math>\overset{\frown}{n},</math><math>\overrightarrow{a}</math> और <math>\overrightarrow{b}</math> दोनों को समाहित करने वाले समतल पर लंबवत इकाई सदिश है। दो सदिशों का वज्र गुणनफल सूत्र द्वारा दिया जाता है: | |||
<math>\overrightarrow{a}\times \overrightarrow{b}=|a||b|sin(\theta)\overset{\frown}{n}</math> | |||
== सदिशों के गुणनफल के लिए फलन नियम == | |||
दो सदिशों के गुणनफल, डॉट गुणनफल और वज्र गुणनफल के लिए फलन नियम को नीचे दिए गए वाक्यों से समझा जा सकता है। | |||
=== डॉट गुणनफल === | |||
दो सदिशों के डॉट गुणनफल के लिए, दो सदिशों को <math>x, y, z</math> अक्षों के साथ इकाई सदिशों, <math>i, j, k</math> के रूप में व्यक्त किया जाता है, फिर अदिश गुणनफल निम्नानुसार प्राप्त होता है: | |||
यदि <math>\overrightarrow{a }=a_1\overset{\frown}{i}+b_1\overset{\frown}{j}+c_1\overset{\frown}{k}</math> और <math>\overrightarrow{b }=a_2\overset{\frown}{i}+b_2\overset{\frown}{j}+c_2\overset{\frown}{k}</math> तब | |||
<math>\overrightarrow{a}\cdot \overrightarrow{b} = (a_1\overset{\frown}{i}+b_1\overset{\frown}{j}+c_1\overset{\frown}{k})(a_2\overset{\frown}{i}+b_2\overset{\frown}{j}+c_2\overset{\frown}{k})</math> | |||
<math>=(a_1a_2)(\overset{\frown}{i}.\overset{\frown}{i})+(a_1b_2)({\overset{\frown}{i}}.\overset{\frown}{j})+(a_1c_2)(\overset{\frown}{i}.\overset{\frown}{k})+(b_1a_2)(\overset{\frown}{j}.{\overset{\frown}{i}})+(b_1b_2)({\overset{\frown}{j}}.\overset{\frown}{j})+(b_1c_2(\overset{\frown}{j}.\overset{\frown}{k})+(c_1a_2)(\overset{\frown}{k}.\overset{\frown}{i})+(c_1b_2)(\overset{\frown}{k}.\overset{\frown}{j})+(c_1c_2)(\overset{\frown}{k}.\overset{\frown}{k})\overrightarrow{a}.\overrightarrow{b}</math> | |||
<math>= a_1a_2+b_1b_2+c_1c_2</math> | |||
=== वज्र गुणनफल === | |||
मान लें कि <math>\overrightarrow{a}</math> और <math>\overrightarrow{b}</math> दो सदिश हैं, जैसे कि <math>\overrightarrow{a }=a_1\overset{\frown}{i}+b_1\overset{\frown}{j}+c_1\overset{\frown}{k}</math> और <math>\overrightarrow{b }=a_2\overset{\frown}{i}+b_2\overset{\frown}{j}+c_2\overset{\frown}{k}</math> तो निर्धारकों का उपयोग करके, हम वज्र गुणनफल पा सकते हैं और परिणाम को निम्नलिखित आव्यूह संकेतन का उपयोग करके वज्र गुणनफल सूत्र के रूप में लिख सकते हैं। | |||
दो सदिशों के वज्र गुणनफल को वज्र गुणनफल सूत्र का उपयोग करके भी दर्शाया जाता है: | |||
<math>\overrightarrow{a} \times \overrightarrow{b}=\overset{\frown}{i}(b_1c_2- b_2c_1)-\overset{\frown}{j}(a_1c_2-a_2c_1)+\overset{\frown}{k}(a_1b_2-a_2b_1)</math> | |||
ध्यान दे : <math>{\overset{\frown}{i }},{\overset{\frown}{j}}</math> और <math>{\overset{\frown}{k}}</math> क्रमशः <math>x</math>-अक्ष, <math>y</math>-अक्ष, और <math>z</math>-अक्ष की दिशा में इकाई सदिश हैं। | |||
== सदिशों के गुणनफल के गुणधर्म == | |||
इकाई सदिश के डॉट गुणनफल का अध्ययन इकाई सदिशों <math>\overset{\frown}{i}</math> को <math>x</math>-अक्ष के साथ, <math>\overset{\frown}{j}</math> को <math>y</math>-अक्ष के साथ, और <math>\overset{\frown}{k}</math> को <math>z</math>-अक्ष के साथ क्रमशः लेकर किया जाता है। इकाई सदिशों <math>\overset{\frown}{i},\overset{\frown}{j},\overset{\frown}{k}</math> का डॉट गुणनफल सदिशों के डॉट गुणनफल के समान नियमों का पालन करता है। समान सदिशों के बीच का कोण <math>0^\circ</math> के बराबर है, और इसलिए उनका डॉट गुणनफल <math>0</math> के बराबर है। और दो लंबवत सदिशों के बीच का कोण <math>90^\circ</math> है, और उनका डॉट गुणनफल <math>0</math> के बराबर है। | |||
* <math>\overset{\frown}{i}.\overset{\frown}{i} = \overset{\frown}{j}.{\overset{\frown}{j}} = \overset{\frown}{k}.\overset{\frown}{k}= 1</math> | |||
* <math>\overset{\frown}{i}.\overset{\frown}{j} = \overset{\frown}{j}.\overset{\frown}{k} = \overset{\frown}{k}.{\overset{\frown}{i}}= 0</math> | |||
इकाई सदिशों का वज्र गुणनफल | |||
<math>\overset{\frown}{i},\overset{\frown}{j},\overset{\frown}{k}</math> सदिशों के वज्र गुणनफल के समान नियमों का पालन करता है। समान सदिशों के बीच का कोण <math>0^\circ</math> के बराबर है, और इसलिए उनका वज्र गुणनफल <math>0</math> के बराबर है। और दो लंबवत सदिशों के बीच का कोण <math>90^\circ</math> है, और उनका वज्र गुणनफल एक सदिश देता है, जो दो दिए गए सदिशों के लंबवत है। | |||
* <math>\overrightarrow{i}\times \overrightarrow{i}=\overrightarrow{j}\times \overrightarrow{j}={\overrightarrow{k}}\times \overrightarrow{k}=0</math> | |||
[[File:सदिशों के गुणनफल के गुणधर्म.jpg|thumb|280x280px|सदिशों के गुणनफल के गुणधर्म]] | |||
दो सदिशों का वज्र गुणनफल एक चक्रीय क्रम का अनुसरण करता है जैसा कि नीचे दी गई छवि में है। चक्रीय अनुक्रम में दो सदिशों का वज्र गुणनफल अनुक्रम में तीसरा सदिश देता है। | |||
* <math>\overrightarrow{i}\times \overrightarrow{j}=\overrightarrow{k};\overrightarrow{j}\times \overrightarrow{k}=\overrightarrow{i};\overrightarrow{k}\times \overrightarrow{i}=\overrightarrow{j}</math> | |||
* <math>\overrightarrow{j}\times \overrightarrow{i}=\overrightarrow{-k};\overrightarrow{k}\times \overrightarrow{j}=\overrightarrow{-i};\overrightarrow{i}\times \overrightarrow{k}=\overrightarrow{-j}</math> | |||
सदिशों के गुणनफल के गुण सदिश गुणन की विस्तृत समझ प्राप्त करने और सदिशों से संबंधित अनेक गणनाएं करने में सहायक होते हैं। सदिशों के गुणनफल के कुछ महत्वपूर्ण गुण यहां सूचीबद्ध हैं। | |||
* दो सदिशों का वज्र गुणनफल सूत्र द्वारा दिया जाता है <math>\overrightarrow{a}\times \overrightarrow{b}=|a||b|sin(\theta)</math> | |||
* दो सदिशों का डॉट गुणनफल सूत्र द्वारा दिया जाता है <math>\overrightarrow{a}\cdot \overrightarrow{b}=|a||b|cos(\theta)</math> | |||
* दो सदिशों का डॉट गुणनफल क्रमविनिमेय गुण का अनुसरण करता है। <math>\overrightarrow{a}\cdot \overrightarrow{b}=\overrightarrow{b}\cdot \overrightarrow{a}</math> | |||
* दो सदिशों का वज्र -गुणनफल न क्रमविनिमेय गुण का पालन नहीं करता है। <math>\overrightarrow{a}\times \overrightarrow{b}\neq \overrightarrow{b} \times \overrightarrow{a}</math> | |||
* प्रति-विनिमेय गुण: <math>\overrightarrow{a}\times \overrightarrow{b}= \overrightarrow{-b} \times \overrightarrow{a}</math> | |||
* वितरणात्मक गुण: <math>\overrightarrow{a}\times ( \overrightarrow{b}+ \overrightarrow{c}) = (\overrightarrow{a} \times \overrightarrow{b}) +(\overrightarrow{a}\times \overrightarrow{c})</math> | |||
* शून्य सदिश का वज्र गुणनफल : <math>{\overrightarrow{a}}\times \overrightarrow{0}=\overrightarrow{0}</math> | |||
* सदिश का स्वयं सदिश के साथ वज्र गुणनफल : <math>{\overrightarrow{a}}\times \overrightarrow{a}=\overrightarrow{0}</math> | |||
* एक अदिश राशि से गुणा: <math>c(\overrightarrow{a}\times \overrightarrow{b})=c\overrightarrow{a}\times \overrightarrow{b}=\overrightarrow{a}\times c\overrightarrow{b}</math> | |||
* दो सदिशों का डॉट गुणनफल एक अदिश राशि है और दो सदिशों के तल में स्थित होता है। | |||
* दो सदिशों का वज्र गुणनफल एक सदिश है, जो इन दो सदिशों वाले तल के लंबवत होता है। | |||
== ट्रिपल वज्र गुणनफल == | |||
किसी सदिश का अन्य दो सदिश के वज्र गुणनफल के साथ वज्र गुणनफल सदिश का ट्रिपल वज्र गुणनफल है। ट्रिपल वज्र गुणनफल का परिणाम एक सदिश है। ट्रिपल वज्र सदिश का परिणाम दिए गए तीन सदिश के तल में स्थित है। यदि <math>a, b,</math>और <math>c</math> सदिश हैं, तो इन सदिश का सदिश ट्रिपल गुणनफल इस रूप का होगा: | |||
<math>(\overrightarrow{a}\times \overrightarrow{b})\times \overrightarrow{c}=(\overrightarrow{a}\cdot \overrightarrow{c})\overrightarrow{b}-(\overrightarrow{b}\cdot \overrightarrow{c})\overrightarrow{a}</math> | |||
== उदाहरण == | |||
'''उदाहरण:''' दो सदिशों <math>\overrightarrow{a}=(3,4,5)</math> और <math>\overrightarrow{b}=(7,8,9)</math> का वज्र गुणनफल ज्ञात कीजिए | |||
'''समाधान''': वज्र गुणनफल इस प्रकार दिया गया है, | |||
<math>\overrightarrow{a}=(3,4,5)</math> <math>\times</math> <math>\overrightarrow{b}=(7,8,9)</math> | |||
<math>a \times b= \begin{matrix} \overset{\frown}{i} & \overset{\frown}{j} & \overset{\frown}{k} \\ 3 & 4 & 5 \\ 7 & 8 & 9 \end{matrix}</math> | |||
<math>= [(4\times 9)-(5\times 8)] \overset{\frown}{i} -[(3\times 9)-(5\times 7)]\overset{\frown}{j}+[(3\times 8)-(4\times 7)] \overset{\frown}{k}</math> | |||
<math>= (36-40)\overset{\frown}{i} -(27-35)\overset{\frown}{\overset{\frown}{j}} +(24-28) \overset{\frown}{k}</math> | |||
<math>= -4\overset{\frown}{i} + 8\overset{\frown}{j} -4\overset{\frown}{k}</math> | |||
'''उत्तर''': अतः, <math>a \times b=-4\overset{\frown}{i}+8\overset{\frown}{j}-4\overset{\frown}{k}</math> | |||
[[Category:सदिश बीजगणित]][[Category:गणित]][[Category:कक्षा-12]] | [[Category:सदिश बीजगणित]][[Category:गणित]][[Category:कक्षा-12]] | ||
Latest revision as of 08:52, 15 December 2024
सदिशों का गुणनफल दो प्रकार का होता है। सदिश में परिमाण और दिशा दोनों होते हैं और इसके आधार पर सदिशों के दो गुणनफल होते हैं, दो सदिशों का डॉट गुणनफल और दो सदिशों का वज्र गुणनफल। दो सदिशों के डॉट गुणनफल को अदिश गुणनफल भी कहा जाता है, क्योंकि परिणामी मान एक अदिश राशि होती है। वज्र गुणनफल को सदिश गुणनफल कहा जाता है क्योंकि परिणाम एक सदिश होता है, जो इन दो सदिशों के लंबवत होता है।
आइए सदिशों के दो गुणनफल, फलन नियम, गुण, उपयोग, सदिशों के इन गुणनफलों के उदाहरणों के बारे में जानें।
परिभाषा
एक सदिश में परिमाण और दिशा दोनों होते हैं। हम दो या अधिक सदिशों को डॉट गुणनफल और वज्र गुणनफल से गुणा कर सकते हैं। आइए सदिशों के प्रत्येक गुणनफल के बारे में अधिक समझें।
डॉट गुणनफल
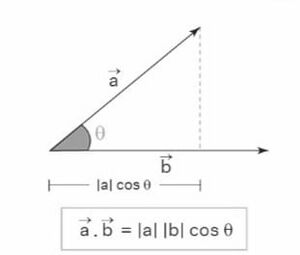
सदिशों के डॉट गुणनफल को सदिशों का अदिश गुणनफल भी कहा जाता है। सदिशों के डॉट गुणनफल का परिणाम एक अदिश मान होता है। सदिशों का डॉट गुणनफल दो सदिशों के परिमाणों के गुणनफल और दो सदिशों के बीच के कोण के कोसाइन के बराबर होता है। दो सदिशों के डॉट गुणनफल का परिणाम दो सदिशों के एक ही तल में होता है। डॉट गुणनफल एक सकारात्मक वास्तविक संख्या या एक नकारात्मक वास्तविक संख्या हो सकती है।
मान लीजिए कि और दो शून्येतर सदिश हैं, और सदिशों का सम्मिलित कोण है। तब अदिश गुणनफल या डॉट गुणनफल को द्वारा दर्शाया जाता है, जिसे इस प्रकार परिभाषित किया जाता है:
यहाँ, का परिमाण है, का परिमाण है, तथा उनके बीच का कोण है।
वज्र गुणनफल
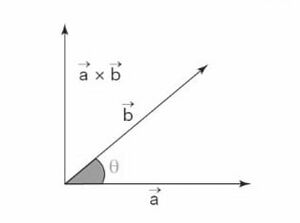
वज्र गुणनफल को सदिश गुणनफल भी कहा जाता है। वज्र गुणनफल सदिश गुणन का एक रूप है, जो अलग-अलग प्रकृति या प्रकार के दो सदिश के बीच किया जाता है। जब दो सदिश को एक दूसरे से गुणा किया जाता है और गुणनफल भी एक सदिश मात्रा होती है, तो परिणामी सदिश को दो सदिश का वज्र गुणनफल या सदिश गुणनफल कहा जाता है। परिणामी सदिश दो दिए गए सदिश वाले समतल के लंबवत होता है।
हम इसे एक उदाहरण से समझ सकते हैं कि यदि हमारे पास समतल में स्थित दो सदिश हैं, तो उनका वज्र गुणनफल -अक्ष की दिशा में एक परिणामी सदिश देगा, जो समतल के लंबवत है। मूल सदिशों के बीच चिह्न का उपयोग किया जाता है। दो सदिशों का सदिश गुणनफल या वज्र गुणनफल इस प्रकार दिखाया जाता है:
यहाँ और दो सदिश हैं, और परिणामी सदिश है। मान लें कि , और के बीच बना कोण है और और दोनों को समाहित करने वाले समतल पर लंबवत इकाई सदिश है। दो सदिशों का वज्र गुणनफल सूत्र द्वारा दिया जाता है:
सदिशों के गुणनफल के लिए फलन नियम
दो सदिशों के गुणनफल, डॉट गुणनफल और वज्र गुणनफल के लिए फलन नियम को नीचे दिए गए वाक्यों से समझा जा सकता है।
डॉट गुणनफल
दो सदिशों के डॉट गुणनफल के लिए, दो सदिशों को अक्षों के साथ इकाई सदिशों, के रूप में व्यक्त किया जाता है, फिर अदिश गुणनफल निम्नानुसार प्राप्त होता है:
यदि और तब
वज्र गुणनफल
मान लें कि और दो सदिश हैं, जैसे कि और तो निर्धारकों का उपयोग करके, हम वज्र गुणनफल पा सकते हैं और परिणाम को निम्नलिखित आव्यूह संकेतन का उपयोग करके वज्र गुणनफल सूत्र के रूप में लिख सकते हैं।
दो सदिशों के वज्र गुणनफल को वज्र गुणनफल सूत्र का उपयोग करके भी दर्शाया जाता है:
ध्यान दे : और क्रमशः -अक्ष, -अक्ष, और -अक्ष की दिशा में इकाई सदिश हैं।
सदिशों के गुणनफल के गुणधर्म
इकाई सदिश के डॉट गुणनफल का अध्ययन इकाई सदिशों को -अक्ष के साथ, को -अक्ष के साथ, और को -अक्ष के साथ क्रमशः लेकर किया जाता है। इकाई सदिशों का डॉट गुणनफल सदिशों के डॉट गुणनफल के समान नियमों का पालन करता है। समान सदिशों के बीच का कोण के बराबर है, और इसलिए उनका डॉट गुणनफल के बराबर है। और दो लंबवत सदिशों के बीच का कोण है, और उनका डॉट गुणनफल के बराबर है।
इकाई सदिशों का वज्र गुणनफल
सदिशों के वज्र गुणनफल के समान नियमों का पालन करता है। समान सदिशों के बीच का कोण के बराबर है, और इसलिए उनका वज्र गुणनफल के बराबर है। और दो लंबवत सदिशों के बीच का कोण है, और उनका वज्र गुणनफल एक सदिश देता है, जो दो दिए गए सदिशों के लंबवत है।
दो सदिशों का वज्र गुणनफल एक चक्रीय क्रम का अनुसरण करता है जैसा कि नीचे दी गई छवि में है। चक्रीय अनुक्रम में दो सदिशों का वज्र गुणनफल अनुक्रम में तीसरा सदिश देता है।
सदिशों के गुणनफल के गुण सदिश गुणन की विस्तृत समझ प्राप्त करने और सदिशों से संबंधित अनेक गणनाएं करने में सहायक होते हैं। सदिशों के गुणनफल के कुछ महत्वपूर्ण गुण यहां सूचीबद्ध हैं।
- दो सदिशों का वज्र गुणनफल सूत्र द्वारा दिया जाता है
- दो सदिशों का डॉट गुणनफल सूत्र द्वारा दिया जाता है
- दो सदिशों का डॉट गुणनफल क्रमविनिमेय गुण का अनुसरण करता है।
- दो सदिशों का वज्र -गुणनफल न क्रमविनिमेय गुण का पालन नहीं करता है।
- प्रति-विनिमेय गुण:
- वितरणात्मक गुण:
- शून्य सदिश का वज्र गुणनफल :
- सदिश का स्वयं सदिश के साथ वज्र गुणनफल :
- एक अदिश राशि से गुणा:
- दो सदिशों का डॉट गुणनफल एक अदिश राशि है और दो सदिशों के तल में स्थित होता है।
- दो सदिशों का वज्र गुणनफल एक सदिश है, जो इन दो सदिशों वाले तल के लंबवत होता है।
ट्रिपल वज्र गुणनफल
किसी सदिश का अन्य दो सदिश के वज्र गुणनफल के साथ वज्र गुणनफल सदिश का ट्रिपल वज्र गुणनफल है। ट्रिपल वज्र गुणनफल का परिणाम एक सदिश है। ट्रिपल वज्र सदिश का परिणाम दिए गए तीन सदिश के तल में स्थित है। यदि और सदिश हैं, तो इन सदिश का सदिश ट्रिपल गुणनफल इस रूप का होगा:
उदाहरण
उदाहरण: दो सदिशों और का वज्र गुणनफल ज्ञात कीजिए
समाधान: वज्र गुणनफल इस प्रकार दिया गया है,
उत्तर: अतः,