चक्रीय चतुर्भुज: Difference between revisions

Latest revision as of 12:09, 3 November 2024

चक्रीय चतुर्भुज

चक्रीय चतुर्भुज एक वृत्त में अंकित चार भुजाओं वाला बहुभुज होता है। इसमें दी गई भुजाओं की लंबाई के साथ अधिकतम संभव क्षेत्रफल होता है। दूसरे शब्दों में, एक वृत्त में अंकित चतुर्भुज उन भुजाओं की लंबाई के साथ अधिकतम संभव क्षेत्र को दर्शाता है।

चक्रीय चतुर्भुज की परिभाषा

चक्रीय चतुर्भुज का अर्थ है एक चतुर्भुज जो एक वृत्त में अंकित होता है। इसका मतलब है कि एक वृत्त है जो चतुर्भुज के सभी चार शीर्षों से होकर गुजरता है। शीर्षों को चक्रीय कहा जाता है। वृत्त के केंद्र को परिकेंद्र के रूप में जाना जाता है और वृत्त की त्रिज्या को परित्रिज्या के रूप में जाना जाता है।

शब्द "चक्रीय" ग्रीक शब्द "कुक्लोस" से लिया गया है, जिसका अर्थ है "वृत्त" या "पहिया"। शब्द "चतुर्भुज" प्राचीन लैटिन शब्द "क्वाड्री" से लिया गया है, जिसका अर्थ है "चार भुजाएँ" या "लैटस"।

नीचे दिए गए चित्र में, $ABCD$ एक चक्रीय चतुर्भुज है, जिसकी भुजाओं की लंबाई $a,b,c,d$ तथा विकर्ण $p,q$ हैं।

चित्र . 1

चक्रीय चतुर्भुज के गुणधर्म

चक्रीय चतुर्भुज के गुण हमें इस आकृति को आसानी से पहचानने और इस पर आधारित प्रश्नों को हल करने में सहायता करते हैं। चक्रीय चतुर्भुज के कुछ गुण नीचे दिए गए हैं:

चक्रीय चतुर्भुज में, चतुर्भुज के सभी चार शीर्ष वृत्त की परिधि पर स्थित होते हैं।
उत्कीर्ण चतुर्भुज की चारों भुजाएँ वृत्त की चार जीवाएँ हैं।
किसी शीर्ष पर बाह्य कोण का माप विपरीत आंतरिक कोण के बराबर होता है।
चक्रीय चतुर्भुज में, $p\times q$ = सम्मुख भुजाओं के गुणनफल का योग, जहाँ $p,q$ विकर्ण हैं।
लम्ब समद्विभाजक सदैव समवर्ती होते हैं।
चक्रीय चतुर्भुज की चारों भुजाओं के लंबवत समद्विभाजक केंद्र $O$ पर मिलते हैं।
विपरीत कोणों की एक जोड़ी का योग 180∘(पूरक) होता है। मान लीजिए $\angle A,\angle B,\angle C,\angle D$ एक उत्कीर्ण चतुर्भुज के चार कोण हैं। तब, $\angle A+\angle C=180^{\circ }$ तथा $\angle B+\angle D=180^{\circ }$ ।

चक्रीय चतुर्भुज से संबंधित प्रमेय नीचे उल्लिखित हैं।

प्रमेय 1: चक्रीय चतुर्भुज के सम्मुख कोणों के किसी भी युग्म का योग $180^{\circ }$ होता है।

प्रमेय 2: यदि किसी चतुर्भुज के सम्मुख कोणों के युग्म का योग $180^{\circ }$ है, तो चतुर्भुज चक्रीय है।

चक्रीय चतुर्भुज का क्षेत्रफल

चक्रीय चतुर्भुज का क्षेत्रफल ${\sqrt {(s-a)(s-b)(s-c)(s-d)}}$ है जहाँ $a,b,c,d$ चतुर्भुज की चारों भुजाएँ हैं और $s$ अर्ध परिमाप है जिसे $s={\frac {1}{2}}\times (a+b+c+d)$ के रूप में परिकलित किया जा सकता है।

त्रिभुज के लिए हीरोन का सूत्र भी इसी समीकरण से प्राप्त होता है।

उदाहरण

चित्र -2

1: चित्र 2 में, $ABCD$ एक चक्रीय चतुर्भुज है जिसमें $AC$ और $BD$ इसके विकर्ण हैं।

यदि $\angle DBC=55^{\circ }$ और $\angle BAC=45^{\circ }$ हैं , $\angle BCD$ ज्ञात कीजिए

हल:

$\angle CAD=\angle DBC=55^{\circ }$ (एक ही खंड में कोण)

अत:, $\angle DAB=\angle CAD+\angle BAC$

$\angle DAB=55^{\circ }+45^{\circ }=100^{\circ }$

परंतु $\angle DAB+\angle BCD=180^{\circ }$ (चक्रीय चतुर्भुज के विपरीत कोण)

$\angle BCD=180^{\circ }-\angle DAB$

$\angle BCD=180^{\circ }-100^{\circ }=80^{\circ }$

@@ Line 1: / Line 1: @@
+== चक्रीय चतुर्भुज ==
+चक्रीय [[चतुर्भुज]] एक वृत्त में अंकित चार भुजाओं वाला बहुभुज होता है। इसमें दी गई भुजाओं की लंबाई के साथ अधिकतम संभव क्षेत्रफल होता है। दूसरे शब्दों में, एक वृत्त में अंकित चतुर्भुज उन भुजाओं की लंबाई के साथ अधिकतम संभव क्षेत्र को दर्शाता है।
+==चक्रीय चतुर्भुज की परिभाषा ==
+चक्रीय चतुर्भुज का अर्थ है एक चतुर्भुज जो एक वृत्त में अंकित होता है। इसका मतलब है कि एक वृत्त है जो चतुर्भुज के सभी चार शीर्षों से होकर गुजरता है। शीर्षों को चक्रीय कहा जाता है। वृत्त के केंद्र को परिकेंद्र के रूप में जाना जाता है और वृत्त की त्रिज्या को परित्रिज्या के रूप में जाना जाता है।
+शब्द "चक्रीय" ग्रीक शब्द "कुक्लोस" से लिया गया है, जिसका अर्थ है "वृत्त" या "पहिया"। शब्द "चतुर्भुज" प्राचीन लैटिन शब्द "क्वाड्री" से लिया गया है, जिसका अर्थ है "चार भुजाएँ" या "लैटस"।
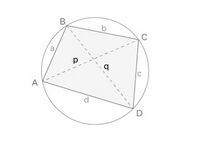
+नीचे दिए गए चित्र में, <math>ABCD</math> एक चक्रीय चतुर्भुज है, जिसकी भुजाओं की लंबाई <math>a,b,c,d</math> तथा विकर्ण <math>p,q</math> हैं।[[File:Cyclic quadrilateral -1.jpg|alt=Fig. 1|none|thumb|200x200px|चित्र . 1]]
+==चक्रीय चतुर्भुज के गुणधर्म==
+चक्रीय चतुर्भुज के गुण हमें इस आकृति को आसानी से पहचानने और इस पर आधारित प्रश्नों को हल करने में सहायता करते हैं। चक्रीय चतुर्भुज के कुछ गुण नीचे दिए गए हैं:
+* चक्रीय चतुर्भुज में, चतुर्भुज के सभी चार शीर्ष वृत्त की परिधि पर स्थित होते हैं।
+* उत्कीर्ण चतुर्भुज की चारों भुजाएँ वृत्त की चार जीवाएँ हैं।
+* किसी शीर्ष पर बाह्य कोण का माप विपरीत आंतरिक कोण के बराबर होता है।
+* चक्रीय चतुर्भुज में, <math>p \times q</math>= सम्मुख भुजाओं के गुणनफल का योग, जहाँ <math>p,q</math> विकर्ण हैं।
+* लम्ब समद्विभाजक सदैव समवर्ती होते हैं।
+* चक्रीय चतुर्भुज की चारों भुजाओं के लंबवत समद्विभाजक केंद्र <math>O</math> पर मिलते हैं।
+* विपरीत कोणों की एक जोड़ी का योग 180∘(पूरक) होता है। मान लीजिए <math>\angle A,\angle B,\angle C,\angle D</math> एक उत्कीर्ण चतुर्भुज के चार कोण हैं। तब,<math>\angle A+\angle C =180^\circ</math> तथा <math>\angle B+\angle D =180^\circ</math>।
+चक्रीय चतुर्भुज से संबंधित प्रमेय नीचे उल्लिखित हैं।
+प्रमेय 1: चक्रीय चतुर्भुज के सम्मुख कोणों के किसी भी युग्म का योग <math>180^\circ</math> होता है।
+प्रमेय 2: यदि किसी चतुर्भुज के सम्मुख कोणों के युग्म का योग <math>180^\circ</math> है, तो चतुर्भुज चक्रीय है।
+==चक्रीय चतुर्भुज का क्षेत्रफल==
+चक्रीय चतुर्भुज का क्षेत्रफल <math>\sqrt{(s-a)(s-b)(s-c)(s-d)}</math> है जहाँ <math>a,b,c,d</math> चतुर्भुज की चारों भुजाएँ हैं और <math>s</math> अर्ध परिमाप है जिसे <math>s=\frac{1}{2} \times (a+b+c+d)</math> के रूप में परिकलित किया जा सकता है।
+त्रिभुज के लिए [[हीरोन का सूत्र]] भी इसी समीकरण से प्राप्त होता है।
+== उदाहरण ==
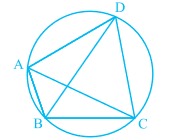
+[[File:Cyclic quadrilateral - 2.jpg|alt=Fig. 2|thumb|चित्र -2]]
+: चित्र 2 में, <math>ABCD</math> एक चक्रीय चतुर्भुज है जिसमें <math>AC</math> और <math>BD</math> इसके विकर्ण हैं।
+यदि <math>\angle DBC =55^\circ</math>और <math>\angle BAC =45^\circ</math>हैं , <math>\angle BCD</math> ज्ञात कीजिए
+हल:
+<math>\angle CAD=\angle DBC =55^\circ</math>(एक ही खंड में कोण)
+अत:, <math>\angle DAB=\angle CAD+\angle BAC</math>
+<math>\angle DAB=55^\circ +45^\circ=100^\circ</math>
+परंतु <math>\angle DAB+\angle BCD = 180^\circ</math>(चक्रीय चतुर्भुज के विपरीत कोण)
+<math>\angle BCD = 180^\circ -\angle DAB</math>
+<math>\angle BCD = 180^\circ -100^\circ =80^\circ</math>
 [[Category:वृत्त]][[Category:कक्षा-9]][[Category:गणित]]
-Cyclic Quadrilaterals