ब्रह्मगुप्त: Difference between revisions

Latest revision as of 12:50, 18 September 2023

ब्रह्मगुप्त के गणितीय योगदान के पूर्व, उनके जीवन परिचय के बारे में जानते हैं ।

ब्रह्मगुप्त एक प्राचीन भारतीय खगोलशास्त्री और गणितज्ञ थे । ^[1]इनका जन्म $597$ ईस्वी में हुआ, तथा यह $668$ ईस्वी तक जीवित रहे । इनका जन्म उत्तर पश्चिम भारत के भीनमाल शहर में हुआ था। इसी कारण उन्हें ' भिल्लमालाआचार्य ' के नाम से भी कई जगह उल्लेखित किया गया है। यह शहर तत्कालीन गुजरात प्रदेश की राजधानी तथा हर्षवर्धन साम्राज्य के राजा व्याघ्रमुख के समकालीन माना जाता है। उनके पिता, जिनका नाम जिस्नुगुप्ता था, एक ज्योतिषी थे। हालाँकि ब्रह्मगुप्त खुद को एक खगोलशास्त्री मानते थे, जिन्होंने कुछ योगदान गणित में किया था, लेकिन अब उन्हें मुख्य रूप से गणित में उनके योगदान के लिए स्मरण किया जाता है ।

महत्वपूर्ण योगदान

ब्रह्मगुप्त ने उज्जैन में रहने के दौरान कई गणितीय और खगोलीय पाठ्यपुस्तकें लिखीं, जिनमें दुर्केमिनार्डा, खंडखाद्यक, ब्रह्मस्फुटसिद्धांत और कैडमकेला सम्मिलित हैं। उन्होंने कई गणितीय सूत्र विकसित किए और कुछ खगोलीय रूप से महत्वपूर्ण मापदंडों की गणना की।
ब्रह्मगुप्त ने तर्क दिया कि पृथ्वी गोल है, चपटी नहीं, जैसा कि बहुत से लोग अब भी मानते हैं।
ब्रह्मगुप्त ने $628$ ईस्वी में $30$ वर्ष की आयु में अपनी सबसे प्रसिद्ध पुस्तक, ब्रह्मस्फुटसिद्धांत, जिसका अर्थ है "ब्रह्मा का संशोधित ग्रंथ" की रचना की। इस पुस्तक में संस्कृत में $1008$ श्लोकों के साथ पच्चीस अध्याय हैं। विद्वानों का मानना है कि इस पुस्तक में उनके कई मौलिक कार्य और गणनाएँ सम्मिलित हैं।

ब्रह्मगुप्त का गणित में योगदान

शून्य का परिचय

गणित में ब्रह्मगुप्त के सबसे महत्वपूर्ण योगदानों में से एक शून्य को अपने आप में एक संख्या के रूप में पेश करना था । इससे पहले, यूनानियों और रोमनों ने नोटिंग का प्रतिनिधित्व करने के लिए प्रतीकों का उपयोग किया था, और बेबीलोनियों ने मात्रा की कमी के कारण संकेत के रूप में एक शंख का उपयोग किया था । ब्रह्मस्फुटसिद्धांत सबसे पहला ज्ञात पाठ है जिसने गणितीय हेरफेर के लिए नियम स्थापित किए जो शून्य पर लागू होते हैं ।

ब्रह्मगुप्त ने शून्य के गुणों को इस प्रकार सूचीबद्ध किया ।

जब हम किसी संख्या को उसी से घटाते हैं तो हमें शून्य प्राप्त होता है ।
किसी भी संख्या को शून्य से विभाजित करने पर शून्य परिणाम प्राप्त होता है ।
शून्य को शून्य से विभाजित करने पर शून्य के बराबर होता है ।

ऋणात्मक संख्याओं की अवधारणा

ब्रह्मगुप्त ने सकारात्मक संख्याओं, जिन्हें वे भाग्य कहते थे, की तुलना में नकारात्मक संख्याओं की अवधारणा भी पेश की, जिसे उन्होंने ऋण कहा। उन्होंने समीकरणों में ऋणात्मक संख्याओं से निपटने के लिए बुनियादी गणितीय नियम स्थापित किए । एक उदाहरण इस नियम को संदर्भित करता है कि एक धनात्मक और एक ऋणात्मक संख्या का गुणनफल भी ऋणात्मक होगा। ब्रह्मगुप्त ने गुणों को इस प्रकार सूचीबद्ध किया ।

दो ऋणों का गुणनफल या भागफल एक भाग्य होता है।
ऋण और संपत्ति का गुणनफल या भागफल ऋण होता है।
भाग्य और ऋण का गुणनफल या भागफल ऋण होता है
शून्य से घटाया गया ऋण एक भाग्य है।
शून्य से घटाया गया भाग्य ऋण है।
किसी ऋण या संपत्ति से गुणा किया गया शून्य का गुणनफल शून्य होता है।
दो भाग्य का गुणनफल या भागफल एक भाग्य होता है।

ब्रह्मगुप्त की गुणन विधि

उन्होंने अपनी पुस्तक "ब्रह्मस्फुटसिद्धांत" में गुणन की एक विधि, "गोमूत्रिका" प्रस्तावित की ।

मध्यवर्ती समीकरण

ब्रह्मगुप्त ने $ax+by=c$ प्रकार के समीकरणों को हल करने के लिए कुछ तरीके प्रस्तावित किए। मजूमदार के अनुसार, ब्रह्मगुप्त ने ऐसे समीकरणों को हल करने के लिए निरंतर भिन्नों का उपयोग किया। उन्होंने ${\textstyle ax^{2}+c=y^{2}}$ प्रकार के द्विघात समीकरणों को हल करने का भी प्रयास किया।

ब्रह्मगुप्त का सूत्र

चक्रीय चतुर्भुज ABCD

चक्रीय चतुर्भुज के लिए ब्रह्मगुप्त का सूत्र ज्यामिति में उनकी सबसे प्रसिद्ध खोज माना जाता है। चक्रीय चतुर्भुज की भुजाओं को देखते हुए, उन्होंने चक्रीय चतुर्भुज के क्षेत्रफल के लिए एक अनुमानित और सटीक सूत्र प्रदान किया ।

दिए गए चित्र में, $p,q,r,s$ चक्रीय चतुर्भुज की भुजाएँ हैं ।

इसका अनुमानित क्षेत्रफल $\left[{\frac {p+r}{2}}\times {\frac {q+s}{2}}\right]$ द्वारा दिया गया है ।

जबकि, सटीक क्षेत्रफल ${\sqrt {(t-p)(t-q)(t-r)(t-s)}}$

जहां, $t={\frac {p+q+r+s}{2}}$

$t=$ चतुर्भुज की अर्धपरिधि

क्षेत्रमिति और निर्माण

ब्रह्मगुप्त ने मुख्य रूप से समकोण त्रिभुजों की सहायता से समद्विबाहु त्रिभुज, विषमबाहु त्रिभुज, आयत, समद्विबाहु समलंब, तीन समान भुजाओं वाले समद्विबाहु समलंब और विषमबाहु चक्रीय चतुर्भुज जैसी आकृतियाँ बनाने का प्रयास किया। उन्होंने $\pi$ के मान का अनुमान लगाने के बाद कुछ आकृतियों का आयतन और सतह क्षेत्र भी दिया। उन्होंने आयताकार प्रिज्म, पिरामिड और वर्गाकार पिरामिड के छिन्नक का आयतन ज्ञात किया।

संदर्भ

↑ "ब्रह्मगुप्त का जीवन परिचय".

[1] "ब्रह्मगुप्त का जीवन परिचय".

[1]

@@ Line 3: / Line 3: @@
 [[Category:गणित]]
 [[Category:कक्षा-10]]
-ब्रह्मगुप्त के गणितीय योगदान के पूर्व लिए जानते हैं, उनके जीवन परिचय के बारे में -
+[[Category:Vidyalaya Completed]]
+ब्रह्मगुप्त के गणितीय योगदान के पूर्व, उनके जीवन परिचय के बारे में जानते हैं ।
-[[wikipedia:Brahmagupta|ब्रह्मगुप्त]] एक प्राचीन भारतीय खगोलशास्त्री और गणितज्ञ थे । इनका जन्म 597 ईस्वी में हुआ, तथा यह 668 ई तक जीवित रहे ।  इनका  जन्म उत्तर पश्चिम भारत के भीनमाल शहर में हुआ था।  इसी कारण उन्हें ' भिल्लमालाआचार्य ' के नाम से भी कई जगह उल्लेखित किया गया है। यह शहर तत्कालीन गुजरात प्रदेश की राजधानी तथा हर्षवर्धन साम्राज्य के राजा व्याघ्रमुख के समकालीन माना जाता है।  उनके पिता, जिनका नाम जिस्नुगुप्ता था, एक ज्योतिषी थे। हालाँकि ब्रह्मगुप्त खुद को एक खगोलशास्त्री मानते थे, जिन्होंने कुछ योगदान गणित  में किया था, लेकिन अब उन्हें मुख्य रूप से गणित में उनके योगदान के लिए याद किया जाता है।
+ब्रह्मगुप्त एक प्राचीन भारतीय खगोलशास्त्री और गणितज्ञ थे । <ref>{{Cite web|url=https://en.wikipedia.org/wiki/Brahmagupta|title=ब्रह्मगुप्त का जीवन परिचय}}</ref>इनका जन्म <math>597</math> ईस्वी में हुआ, तथा यह <math>668</math> ईस्वी तक जीवित रहे । इनका  जन्म उत्तर पश्चिम भारत के भीनमाल शहर में हुआ था।  इसी कारण उन्हें ' भिल्लमालाआचार्य ' के नाम से भी कई जगह उल्लेखित किया गया है। यह शहर तत्कालीन गुजरात प्रदेश की राजधानी तथा हर्षवर्धन साम्राज्य के राजा व्याघ्रमुख के समकालीन माना जाता है।  उनके पिता, जिनका नाम जिस्नुगुप्ता था, एक ज्योतिषी थे। हालाँकि ब्रह्मगुप्त खुद को एक खगोलशास्त्री मानते थे, जिन्होंने कुछ योगदान गणित में किया था, लेकिन अब उन्हें मुख्य रूप से गणित में उनके योगदान के लिए स्मरण किया जाता है ।
 == महत्वपूर्ण योगदान ==
-# ब्रह्मगुप्त ने उज्जैन में रहने के दौरान कई गणितीय और खगोलीय पाठ्यपुस्तकें लिखीं, जिनमें दुर्केमिनार्डा, खंडखाद्यक, ब्रह्मस्फुटसिद्धांत और कैडमकेला शामिल हैं। उन्होंने कई गणितीय सूत्र विकसित किए और कुछ खगोलीय रूप से महत्वपूर्ण मापदंडों की गणना की।
+# ब्रह्मगुप्त ने उज्जैन में रहने के दौरान कई गणितीय और खगोलीय पाठ्यपुस्तकें लिखीं, जिनमें ''दुर्केमिनार्डा, खंडखाद्यक, ब्रह्मस्फुटसिद्धांत'' और ''कैडमकेला''  सम्मिलित हैं। उन्होंने कई गणितीय सूत्र विकसित किए और कुछ खगोलीय रूप से महत्वपूर्ण मापदंडों की गणना की।
 # ब्रह्मगुप्त ने तर्क दिया कि पृथ्वी गोल है, चपटी नहीं, जैसा कि बहुत से लोग अब भी मानते हैं।
-# ब्रह्मगुप्त ने 628 ईस्वी में 30 वर्ष की आयु में अपनी सबसे प्रसिद्ध पुस्तक, ब्रह्मस्फुटसिद्धांत, जिसका अर्थ है "ब्रह्मा का संशोधित ग्रंथ" की रचना की। इस पुस्तक में संस्कृत में 1008 श्लोकों के साथ पच्चीस अध्याय हैं। विद्वानों का मानना है कि इस पुस्तक में उनके कई मौलिक कार्य और गणनाएँ शामिल हैं।
+# ब्रह्मगुप्त ने <math>628</math> ईस्वी में <math>30</math> वर्ष की आयु में अपनी सबसे प्रसिद्ध पुस्तक, ब्रह्मस्फुटसिद्धांत, जिसका अर्थ है "ब्रह्मा का संशोधित ग्रंथ" की रचना की। इस पुस्तक में संस्कृत में <math>1008</math> श्लोकों के साथ पच्चीस अध्याय हैं। विद्वानों का मानना है कि इस पुस्तक में उनके कई मौलिक कार्य और गणनाएँ सम्मिलित हैं।
 == ब्रह्मगुप्त का गणित में योगदान ==
 === शून्य का परिचय ===
-गणित में ब्रह्मगुप्त के सबसे महत्वपूर्ण योगदानों में से एक शून्य को अपने आप में एक संख्या के रूप में पेश करना था। इससे पहले, यूनानियों और रोमनों ने नोटिंग का प्रतिनिधित्व करने के लिए प्रतीकों का उपयोग किया था, और बेबीलोनियों ने मात्रा की कमी के कारण संकेत के रूप में एक शंख का उपयोग किया था । ब्रह्मस्फुटसिद्धांत सबसे पहला ज्ञात पाठ है जिसने गणितीय हेरफेर के लिए नियम स्थापित किए जो शून्य पर लागू होते हैं  ।
+गणित में ब्रह्मगुप्त के सबसे महत्वपूर्ण योगदानों में से एक शून्य को अपने आप में एक संख्या के रूप में पेश करना था । इससे पहले, यूनानियों और रोमनों ने नोटिंग का प्रतिनिधित्व करने के लिए प्रतीकों का उपयोग किया था, और बेबीलोनियों ने मात्रा की कमी के कारण संकेत के रूप में एक शंख का उपयोग किया था । ब्रह्मस्फुटसिद्धांत सबसे पहला ज्ञात पाठ है जिसने गणितीय हेरफेर के लिए नियम स्थापित किए जो शून्य पर लागू होते हैं ।
-ब्रह्मगुप्त ने शून्य के गुणों को इस प्रकार सूचीबद्ध किया:1.  जब हम किसी संख्या को उसी से घटाते हैं तो हमें शून्य प्राप्त होता है ।
+ब्रह्मगुप्त ने शून्य के गुणों को इस प्रकार सूचीबद्ध किया ।
-. किसी भी संख्या को शून्य से विभाजित करने पर शून्य परिणाम प्राप्त होता है ।
+# जब हम किसी संख्या को उसी से घटाते हैं तो हमें शून्य प्राप्त होता है ।
+# किसी भी संख्या को शून्य से विभाजित करने पर शून्य परिणाम प्राप्त होता है ।
-. शून्य को शून्य से विभाजित करने पर शून्य के बराबर होता है ।
+# शून्य को शून्य से विभाजित करने पर शून्य के बराबर होता है ।
 === ऋणात्मक संख्याओं की अवधारणा ===
-ब्रह्मगुप्त ने सकारात्मक संख्याओं, जिन्हें वे भाग्य ( fortune) कहते थे, की तुलना में नकारात्मक संख्याओं की अवधारणा भी पेश की, जिसे उन्होंने ऋण (debt) कहा। उन्होंने समीकरणों में ऋणात्मक संख्याओं से निपटने के लिए बुनियादी गणितीय नियम स्थापित किए। एक उदाहरण इस नियम को संदर्भित करता है कि एक धनात्मक और एक ऋणात्मक संख्या का गुणनफल भी ऋणात्मक होगा। ब्रह्मगुप्त ने  गुणों को इस प्रकार सूचीबद्ध किया-
+ब्रह्मगुप्त ने सकारात्मक संख्याओं, जिन्हें वे भाग्य कहते थे, की तुलना में नकारात्मक संख्याओं की अवधारणा भी पेश की, जिसे उन्होंने ऋण कहा। उन्होंने समीकरणों में ऋणात्मक संख्याओं से निपटने के लिए बुनियादी गणितीय नियम स्थापित किए । एक उदाहरण इस नियम को संदर्भित करता है कि एक धनात्मक और एक ऋणात्मक संख्या का गुणनफल भी ऋणात्मक होगा। ब्रह्मगुप्त ने गुणों को इस प्रकार सूचीबद्ध किया ।
-.दो ऋणों का गुणनफल या भागफल एक भाग्य होता है।
+# दो ऋणों का गुणनफल या भागफल एक भाग्य होता है।
+# ऋण और संपत्ति का गुणनफल या भागफल ऋण होता है।
-.ऋण और संपत्ति का गुणनफल या भागफल ऋण होता है।
+# भाग्य और ऋण का गुणनफल या भागफल ऋण होता है
+# शून्य से घटाया गया ऋण एक भाग्य है।
-.भाग्य और ऋण का गुणनफल या भागफल ऋण होता है
+# शून्य से घटाया गया भाग्य ऋण है।
+# किसी ऋण या संपत्ति से गुणा किया गया शून्य का गुणनफल शून्य होता है।
-. शून्य से घटाया गया ऋण एक भाग्य है।
+# दो भाग्य का गुणनफल या भागफल एक भाग्य होता है।
-.शून्य से घटाया गया भाग्य ऋण है।
-.किसी ऋण या संपत्ति से गुणा किया गया शून्य का गुणनफल शून्य होता है।
-. दो भाग्य का गुणनफल या भागफल एक भाग्य होता है।
 === ब्रह्मगुप्त की गुणन विधि ===
@@ Line 48: / Line 43: @@
 === ब्रह्मगुप्त का सूत्र ===
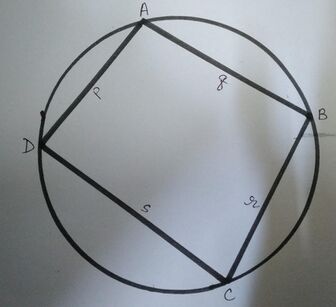
-[[File:चक्रीय चतुर्भुज.jpg|alt=चक्रीय चतुर्भुज|thumb|चक्रीय चतुर्भुज]]
+[[File:चक्रीय चतुर्भुज ABCD.jpg|alt=चक्रीय चतुर्भुज ABCD|thumb|336x336px|चक्रीय चतुर्भुज ABCD]]
-चक्रीय चतुर्भुज के लिए ब्रह्मगुप्त का सूत्र ज्यामिति में उनकी सबसे प्रसिद्ध खोज माना जाता है। चक्रीय चतुर्भुज की भुजाओं को देखते हुए, उन्होंने चक्रीय चतुर्भुज के क्षेत्रफल के लिए एक अनुमानित और सटीक सूत्र प्रदान किया।
+चक्रीय चतुर्भुज के लिए ब्रह्मगुप्त का सूत्र ज्यामिति में उनकी सबसे प्रसिद्ध खोज माना जाता है। चक्रीय चतुर्भुज की भुजाओं को देखते हुए, उन्होंने चक्रीय चतुर्भुज के क्षेत्रफल के लिए एक अनुमानित और सटीक सूत्र प्रदान किया ।
-नीचे दिए गए चित्र में, p, q, r, s चक्रीय चतुर्भुज की भुजाएँ हैं।
-इसका अनुमानित क्षेत्रफल [(p+r) ⁄2 × (q+s) ⁄2]<math>/frac{(p+r)*(q+r)}{2}</math> द्वारा दिया गया है
-जबकि, सटीक क्षेत्रफल √(t − p)(t − q)(t − r)(t − s), जहां, t = (p+q+r+s) ⁄2.
+दिए गए चित्र में,  <math>p, q, r, s</math> चक्रीय चतुर्भुज की भुजाएँ हैं ।
-t= चतुर्भुज का अर्धपरिधि
+इसका अनुमानित क्षेत्रफल   <math>\left [ \frac{p+r}{2}\times\frac{q+s}{2} \right ]</math> द्वारा दिया गया है ।
-इसके अलावा, हेरॉन का सूत्र ब्रह्मगुप्त सूत्र का एक विशेष मामला है, जिसे एक पक्ष को शून्य के बराबर सेट करके प्राप्त किया जा सकता है।
+जबकि, सटीक क्षेत्रफल  <math>\sqrt{(t - p)(t - q)(t - r)(t - s)} </math>
+जहां,  <math>t=\frac{p+q+r+s}{2}</math>
-=== त्रिभुज ===
+<math>t=</math> चतुर्भुज की अर्धपरिधि
-ब्रह्मगुप्त के काम का एक बड़ा हिस्सा ज्यामिति के अध्ययन के लिए समर्पित था। त्रिभुजों के बारे में उनके एक प्रमेय में कहा गया है कि-
-"आधार से विभाजित भुजाओं के वर्गों के अंतर से आधार घटता और बढ़ता है; जब दो से विभाजित किया जाता है तो वे सच्चे खंड होते हैं। लम्बवत् ऊँचाई एक भुजा के वर्ग से उसके खंड के वर्ग से घटाया गया वर्गमूल है।<nowiki>''</nowiki>
+=== क्षेत्रमिति और निर्माण ===
+ब्रह्मगुप्त ने मुख्य रूप से समकोण त्रिभुजों की सहायता से समद्विबाहु त्रिभुज, विषमबाहु त्रिभुज, आयत, समद्विबाहु समलंब, तीन समान  भुजाओं वाले समद्विबाहु समलंब और विषमबाहु चक्रीय चतुर्भुज जैसी आकृतियाँ बनाने का प्रयास किया। उन्होंने <math>\pi</math> के मान का अनुमान लगाने के बाद कुछ आकृतियों का आयतन और सतह क्षेत्र भी दिया। उन्होंने आयताकार प्रिज्म, पिरामिड और वर्गाकार पिरामिड के छिन्नक का आयतन ज्ञात किया।
-=== <sub>क्षेत्रमिति और निर्माण</sub> ===
+== संदर्भ ==
-ब्रह्मगुप्त ने मुख्य रूप से समकोण त्रिभुजों की सहायता से समद्विबाहु त्रिभुज, विषमबाहु त्रिभुज, आयत, समद्विबाहु समलंब, तीन समान  भुजाओं वाले समद्विबाहु समलंब और विषमबाहु चक्रीय चतुर्भुज जैसी आकृतियाँ बनाने का प्रयास किया। उन्होंने π के मान का अनुमान लगाने के बाद कुछ आकृतियों का आयतन और सतह क्षेत्र भी दिया। उन्होंने आयताकार प्रिज्म, पिरामिड और वर्गाकार पिरामिड के छिन्नक का आयतन ज्ञात किया। उन्होंने आगे गड्ढों की एक श्रृंखला की औसत गहराई का प्रस्ताव रखा।
 <references responsive="0" />