अवतल दर्पण द्वारा प्रतिबिंब बनना: Difference between revisions
Listen
m (added Category:प्रकाश -परावर्तन तथा अपवर्तन using HotCat) |
|||
| (14 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
Image formation by Concave Mirror | Image formation by Concave Mirror | ||
अवतल दर्पण एक घुमावदार दर्पण होता है जिसकी परावर्तक सतह अंदर की ओर मुड़ी होती है। यह दर्पण के सापेक्ष वस्तु की स्थिति के आधार पर विभिन्न प्रकार की छवियां बना सकता है। | |||
== दो मुख्य मामले == | |||
एक वास्तविक छवि और एक आभासी छवि। | |||
== वास्तविक छवि == | |||
वास्तविक छवि वह छवि है जो तब बनती है जब वास्तविक प्रकाश किरणें अंतरिक्ष में एक बिंदु पर एकत्रित होती हैं। इसे स्क्रीन पर प्रक्षेपित किया जा सकता है, जिससे यह दृश्यमान हो जाता है। वास्तविक छवि विशिष्ट परिस्थितियों में बनती है जब वस्तु अवतल दर्पण के फोकस बिंदु से परे स्थित होती है। | |||
{|class="wikitable" | |||
|+दर्पण के फोकस बिंदु (अवतल) के सापेक्ष वस्तु की स्थिति की छवि पर प्रभाव(concave) | |||
|- | |||
!width=170px| वस्तु की स्थिति (''S''), <br />केंद्र बिंदु (''F'') | |||
!width=250px| छवि की प्रकृति | |||
!Diagram | |||
|- | |||
!<math>S<F</math> <br />(फोकस बिंदु और दर्पण के बीच वस्तु) | |||
| | |||
* आभासी | |||
* अनुप्रस्थ | |||
* आवर्धित (बड़ा) | |||
| [[File:Concavemirror raydiagram F.svg|250px]] | |||
|- | |||
!<math>S=F</math> <br />(फोकस बिंदु पर वस्तु) | |||
| | |||
* परावर्तित किरणें समानांतर होती हैं और कभी नहीं मिलतीं, इसलिए कोई छवि नहीं बनती है। | |||
* [[सीमा (गणित)|सीमा]] में जहां S, F के पास पहुंचता है, छवि की दूरी [[अनंत]] तक पहुंचती है, और छवि या तो वास्तविक या आभासी हो सकती है और या तो सीधी या उलटी हो सकती है, यह इस बात पर निर्भर करता है कि S अपने बाईं ओर से F तक पहुंचता है या नहीं या दाईं ओर. | |||
| [[File:Concavemirror raydiagram FE.svg|250px]] | |||
|- | |||
!<math>F<S<2F</math><br />(फोकस और वक्रता केंद्र के बीच वस्तु) | |||
| | |||
* वास्तविक छवि | |||
* उलटा (लंबवत) | |||
* आवर्धित (बड़ा) | |||
| [[File:Concavemirror raydiagram 2FE.svg|250px]] | |||
|- | |||
!<math>S=2F</math> <br />(वक्रता के केंद्र पर वस्तु) | |||
| | |||
* वास्तविक छवि | |||
* उलटा (लंबवत) | |||
* एक समान आकार | |||
* प्रतिबिम्ब वक्रता के केन्द्र पर बनता है | |||
| [[File:Image-Concavemirror raydiagram 2F F.svg|250px]] | |||
|- | |||
!<math>S>2F</math><br />(वक्रता केंद्र से परे वस्तु) | |||
| | |||
* वास्तविक छवि | |||
* उलटा (लंबवत) | |||
* कम (कम/छोटा) | |||
* जैसे-जैसे वस्तु की दूरी बढ़ती है, छवि [[असममित रूप से]] केंद्र बिंदु के पास पहुंचती है | |||
* उस सीमा में जहां S अनंत तक पहुंचता है, जैसे-जैसे छवि F के करीब पहुंचती है, छवि का आकार शून्य के करीब पहुंचता है | |||
| [[File:Concavemirror raydiagram 2F.svg|250px]] | |||
|- | |||
|} | |||
== वास्तविक छवि के लिए महत्वपूर्ण अवधारणाएं == | |||
====== फोकल प्वाइंट ====== | |||
[[File:Concave mirror.png|thumb|एक आरेख एक अवतल दर्पण का प्रतिनिधित्व करता है, जो इसका केंद्र बिंदु, w:फोकल लंबाई, w:वक्रता केंद्र और मुख्य अक्ष दिखाता है। यह दर्शकों को यह देखने में सक्षम बनाता है कि दर्पण वास्तव में कैसा दिखता है और कैसे कार्य करता है। यह दर्शक को दिखाता है कि दर्पण उस पर पड़ने वाले प्रकाश को कहां से प्रतिबिंबित करता है, और प्रकाश कहां से प्रतिबिंबित हो सकता है।]] | |||
फोकल प्वाइंट (<math>F</math>) दर्पण के मुख्य अक्ष पर एक बिंदु है जहां प्रकाश की समानांतर किरणें परावर्तन के बाद या तो परिवर्तित होती हैं (अवतल दर्पण के मामले में) या विचलित होती दिखाई देती हैं (उत्तल दर्पण के मामले में) . इसे "एफ" के रूप में दर्शाया गया है। | |||
====== फोकल लंबाई ====== | |||
दर्पण की फोकल लंबाई (<math>f</math>) दर्पण की सतह और उसके फोकस बिंदु के बीच की दूरी है। यह दर्पण की वक्रता त्रिज्या (आरआर) का आधा है। | |||
====== वक्रता केंद्र ====== | |||
वक्रता केंद्र (<math>C</math>) उस गोले का केंद्र है जिसका दर्पण की घुमावदार सतह एक हिस्सा है। यह मुख्य अक्ष पर स्थित है, और दर्पण की वक्रता त्रिज्या दर्पण की सतह से वक्रता केंद्र तक की दूरी है (R=2f)। | |||
== वास्तविक छवि के लिए प्रतिबिंब बनना == | |||
जब किसी वस्तु को अवतल दर्पण के फोकस बिंदु (F) से परे रखा जाता है (अर्थात, वस्तु दर्पण की फोकस दूरी से अधिक दूर होती है), तो दर्पण के एक ही तरफ एक वास्तविक, उलटी और छोटी छवि बनती है। वस्तु के रूप में. | |||
== आभासी छवि == | |||
आभासी छवि वह छवि है जो तब बनती है जब विस्तारित प्रकाश किरणें एक बिंदु से हटती हुई दिखाई देती हैं, लेकिन वे वास्तव में उस बिंदु पर एकत्रित नहीं होती हैं। इसे स्क्रीन पर प्रक्षेपित नहीं किया जा सकता और भौतिक छवि बनाने के अर्थ में यह "वास्तविक" नहीं है। | |||
== आभासी छवि के लिए प्रतिबिंब बनना == | |||
जब किसी वस्तु को फोकस बिंदु (F) और दर्पण की सतह (फोकल लंबाई की तुलना में दर्पण के करीब) के बीच रखा जाता है, तो वस्तु के दर्पण के उसी तरफ एक आभासी, सीधी और आवर्धित छवि बनती है। छवि आभासी है क्योंकि प्रकाश किरणें वास्तव में अभिसरित नहीं होती हैं; वे केवल दर्पण के पीछे एक आभासी बिंदु से हटते हुए प्रतीत होते हैं। | |||
== संक्षेप में == | |||
एक अवतल दर्पण दर्पण के सापेक्ष वस्तु की स्थिति के आधार पर वास्तविक और आभासी दोनों छवियां बना सकता है। दर्पण द्वारा बनाई गई छवि के प्रकार और विशेषताओं को निर्धारित करने के लिए फोकल बिंदु, फोकल लंबाई और वक्रता केंद्र की अवधारणाओं को समझना महत्वपूर्ण है। इन गणनाओं में शामिल गणित अधिक जटिल हो सकता है, लेकिन बुनियादी समझ के लिए, प्रतिबिंब बनना के मूलभूत सिद्धांतों को समझना आवश्यक है। | |||
[[Category:प्रकाश -परावर्तन तथा अपवर्तन]] | [[Category:प्रकाश -परावर्तन तथा अपवर्तन]] | ||
[[Category:कक्षा-10]] | |||
[[Category:भौतिक विज्ञान]] | |||
Latest revision as of 16:31, 25 September 2024
Image formation by Concave Mirror
अवतल दर्पण एक घुमावदार दर्पण होता है जिसकी परावर्तक सतह अंदर की ओर मुड़ी होती है। यह दर्पण के सापेक्ष वस्तु की स्थिति के आधार पर विभिन्न प्रकार की छवियां बना सकता है।
दो मुख्य मामले
एक वास्तविक छवि और एक आभासी छवि।
वास्तविक छवि
वास्तविक छवि वह छवि है जो तब बनती है जब वास्तविक प्रकाश किरणें अंतरिक्ष में एक बिंदु पर एकत्रित होती हैं। इसे स्क्रीन पर प्रक्षेपित किया जा सकता है, जिससे यह दृश्यमान हो जाता है। वास्तविक छवि विशिष्ट परिस्थितियों में बनती है जब वस्तु अवतल दर्पण के फोकस बिंदु से परे स्थित होती है।
| वस्तु की स्थिति (S), केंद्र बिंदु (F) |
छवि की प्रकृति | Diagram |
|---|---|---|
| (फोकस बिंदु और दर्पण के बीच वस्तु) |
|

|
| (फोकस बिंदु पर वस्तु) |
|

|
(फोकस और वक्रता केंद्र के बीच वस्तु) |
|
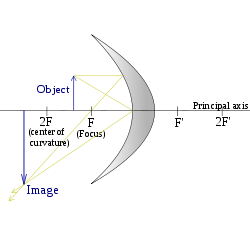
|
| (वक्रता के केंद्र पर वस्तु) |
|

|
(वक्रता केंद्र से परे वस्तु) |
|
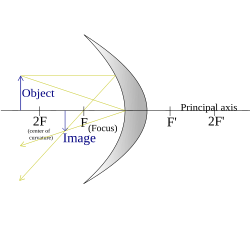
|
वास्तविक छवि के लिए महत्वपूर्ण अवधारणाएं
फोकल प्वाइंट

फोकल प्वाइंट () दर्पण के मुख्य अक्ष पर एक बिंदु है जहां प्रकाश की समानांतर किरणें परावर्तन के बाद या तो परिवर्तित होती हैं (अवतल दर्पण के मामले में) या विचलित होती दिखाई देती हैं (उत्तल दर्पण के मामले में) . इसे "एफ" के रूप में दर्शाया गया है।
फोकल लंबाई
दर्पण की फोकल लंबाई () दर्पण की सतह और उसके फोकस बिंदु के बीच की दूरी है। यह दर्पण की वक्रता त्रिज्या (आरआर) का आधा है।
वक्रता केंद्र
वक्रता केंद्र () उस गोले का केंद्र है जिसका दर्पण की घुमावदार सतह एक हिस्सा है। यह मुख्य अक्ष पर स्थित है, और दर्पण की वक्रता त्रिज्या दर्पण की सतह से वक्रता केंद्र तक की दूरी है (R=2f)।
वास्तविक छवि के लिए प्रतिबिंब बनना
जब किसी वस्तु को अवतल दर्पण के फोकस बिंदु (F) से परे रखा जाता है (अर्थात, वस्तु दर्पण की फोकस दूरी से अधिक दूर होती है), तो दर्पण के एक ही तरफ एक वास्तविक, उलटी और छोटी छवि बनती है। वस्तु के रूप में.
आभासी छवि
आभासी छवि वह छवि है जो तब बनती है जब विस्तारित प्रकाश किरणें एक बिंदु से हटती हुई दिखाई देती हैं, लेकिन वे वास्तव में उस बिंदु पर एकत्रित नहीं होती हैं। इसे स्क्रीन पर प्रक्षेपित नहीं किया जा सकता और भौतिक छवि बनाने के अर्थ में यह "वास्तविक" नहीं है।
आभासी छवि के लिए प्रतिबिंब बनना
जब किसी वस्तु को फोकस बिंदु (F) और दर्पण की सतह (फोकल लंबाई की तुलना में दर्पण के करीब) के बीच रखा जाता है, तो वस्तु के दर्पण के उसी तरफ एक आभासी, सीधी और आवर्धित छवि बनती है। छवि आभासी है क्योंकि प्रकाश किरणें वास्तव में अभिसरित नहीं होती हैं; वे केवल दर्पण के पीछे एक आभासी बिंदु से हटते हुए प्रतीत होते हैं।
संक्षेप में
एक अवतल दर्पण दर्पण के सापेक्ष वस्तु की स्थिति के आधार पर वास्तविक और आभासी दोनों छवियां बना सकता है। दर्पण द्वारा बनाई गई छवि के प्रकार और विशेषताओं को निर्धारित करने के लिए फोकल बिंदु, फोकल लंबाई और वक्रता केंद्र की अवधारणाओं को समझना महत्वपूर्ण है। इन गणनाओं में शामिल गणित अधिक जटिल हो सकता है, लेकिन बुनियादी समझ के लिए, प्रतिबिंब बनना के मूलभूत सिद्धांतों को समझना आवश्यक है।