बहुभुज: Difference between revisions
Jaya agarwal (talk | contribs) |
(added internal links) |
||
| (4 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
बहुभुज एक द्वि-आयामी ज्यामितीय आकृति है जिसमें पक्षों की एक सीमित संख्या होती है। बहुभुज की भुजाएँ एक दूसरे से सिरे से सिरे तक जुड़े हुए सीधी रेखा खंडों से बनी होती हैं। इस प्रकार, बहुभुज के रेखाखंडों को भुजाएँ या किनारे कहा जाता है। वह बिंदु जहाँ दो रेखाखंड मिलते हैं उसे शीर्ष या कोने कहा जाता है, इसलिए एक कोण बनता है। बहुभुज का एक उदाहरण तीन भुजाओं वाला त्रिभुज है। वृत्त भी एक समतल आकृति है लेकिन इसे बहुभुज नहीं माना जाता है, क्योंकि यह एक घुमावदार आकृति है और इसमें भुजाएँ या कोण नहीं होते हैं। इसलिए, हम कह सकते हैं कि सभी बहुभुज <math>2D</math> आकार हैं लेकिन सभी द्वि-आयामी आकृतियाँ बहुभुज नहीं हैं। | |||
== बहुभुज क्या होते हैं? == | |||
बहुभुज | बहुभुज एक बंद आकृति है जो द्वि-आयामी समतल में रेखाखंडों (वक्रों से नहीं) से बनी होती है। बहुभुज दो शब्दों का संयोजन है, यानी पॉली (जिसका अर्थ है कई) और गोन (जिसका अर्थ है भुजाएँ)। | ||
एक बंद आकृति बनाने के लिए, सिरे से सिरे तक जुड़ने के लिए कम से कम तीन रेखा खंडों की आवश्यकता होती है। इस प्रकार न्यूनतम तीन भुजाओं वाले बहुभुज को त्रिभुज के रूप में जाना जाता है और इसे 3-भुज भी कहा जाता है। एक <math>n-</math>पक्षीय बहुभुज को <math>n-</math>भुज कहा जाता है। | |||
== बहुभुज का | '''बहुभुज आकृति''' | ||
भुजाओं और कोणों के आधार पर , बहुभुजों को निम्नलिखित प्रकारों में वर्गीकृत किया जाता है : | |||
परिभाषा के अनुसार, हम जानते हैं कि बहुभुज रेखाखंडों से बना होता है। नीचे कुछ बहुभुजों की आकृतियाँ दी गई हैं जो विभिन्न संख्या में रेखाखंडों से घिरी हुई हैं। | |||
{| class="wikitable" | |||
|+ | |||
|[[File:Triangolo-Scaleno.svg|alt=Triangle|none|thumb|100x100px|त्रिभुज]] | |||
|[[File:Parallelogram1.svg|alt=Parallelogram|none|thumb|100x100px|[[चतुर्भुज]]]] | |||
|[[File:Pentagon.svg|alt=Pentagon|none|thumb|100x100px|पंचकोण]] | |||
|- | |||
|[[File:HexagonWhiteBorder.jpg|alt=Hexagon|none|thumb|100x100px|षटकोण]] | |||
|[[File:Regular octagon.svg|none|thumb|100x100px|अष्टकोण|alt=Octagon]] | |||
| | |||
|} | |||
== बहुभुज के गुणधर्म == | |||
बहुभुजों के गुण उनकी भुजाओं और कोणों पर आधारित होते हैं। | |||
• एक <math>n-</math>भुजा वाले बहुभुज के सभी आंतरिक [[कोण|कोणों]] का योग होता है <math>(n-2) \times 180 ^\circ</math>. | |||
• <math>n-</math>भुजाओं वाले बहुभुज में विकर्णों की संख्या = <math>\frac{n(n-3)}{2}</math> | |||
• किसी बहुभुज के एक कोने से विकर्णों को मिलाने पर बनने वाले त्रिभुजों की संख्या = <math>n-2</math> | |||
• <math>n-</math>भुजा वाले नियमित बहुभुज के प्रत्येक आंतरिक कोण का माप = <math>\frac{(n-2) \times 180 ^\circ}{n}</math> | |||
• एक <math>n-</math>भुजा वाले नियमित बहुभुज के प्रत्येक बाह्य कोण का माप= <math>\frac{360 ^\circ}{n}</math> | |||
== बहुभुज के प्रकार == | |||
भुजाओं और कोणों के आधार पर , बहुभुजों को निम्नलिखित प्रकारों में वर्गीकृत किया जाता है : | |||
# नियमित बहुभुज | # नियमित बहुभुज | ||
| Line 17: | Line 45: | ||
उदाहरण : वर्ग, समबाहु त्रिभुज आदि । | उदाहरण : वर्ग, समबाहु त्रिभुज आदि । | ||
[[File:Square 1.svg|alt=Square|none|thumb|100x100px|वर्ग]] | |||
=== अनियमित बहुभुज === | === अनियमित बहुभुज === | ||
यदि बहुभुज की सभी भुजाएँ और आंतरिक कोण अलग-अलग माप के हों , तो | यदि किसी बहुभुज की सभी भुजाएँ और आंतरिक कोण अलग-अलग माप के हों, तो उसे अनियमित बहुभुज कहते हैं। इसका मतलब है कि या तो भुजाएँ अलग-अलग लंबाई की हैं या कोण अलग-अलग हैं, जो कि बहुभुज को अनियमित कहने के लिए पर्याप्त है। उदाहरण के लिए, एक विषमबाहु त्रिभुज, एक आयत, एक पतंग, आदि। | ||
[[File:Long Rectangle (plain).png|alt=Rectangle|none|thumb|100x100px|आयत( समकोण समानान्तर चतुर्भुज) ]] | |||
उदाहरण | |||
=== उत्तल बहुभुज === | === उत्तल बहुभुज === | ||
यदि किसी बहुभुज के सभी आंतरिक कोण <math>180^\circ</math> से | यदि किसी बहुभुज के सभी आंतरिक कोण <math>180 ^\circ</math> से कम हैं, तो उसे उत्तल बहुभुज के रूप में जाना जाता है। शीर्ष आकृति के केंद्र से बाहर की ओर इंगित करता है। | ||
[[File:Pentagon.svg|alt=Pentagon|none|thumb|100x100px|पंचकोण]] | |||
=== अवतल बहुभुज === | === अवतल बहुभुज === | ||
यदि किसी बहुभुज | यदि किसी बहुभुज के एक या अधिक आंतरिक कोण <math>180 ^\circ</math> से अधिक हैं, तो उसे अवतल बहुभुज के रूप में जाना जाता है। एक अवतल बहुभुज में कम से कम चार भुजाएँ हो सकती हैं। शीर्ष बहुभुज के भीतर की ओर इंगित करता है। | ||
[[File:Concave polygon.jpg|alt=Concave Polygon|none|thumb|300x300px|अवतल बहुभुज]] | |||
[[Category:त्रिभुज]] | |||
[[Category:गणित]] | |||
[[Category:कक्षा-10]] | |||
Latest revision as of 07:48, 5 November 2024
बहुभुज एक द्वि-आयामी ज्यामितीय आकृति है जिसमें पक्षों की एक सीमित संख्या होती है। बहुभुज की भुजाएँ एक दूसरे से सिरे से सिरे तक जुड़े हुए सीधी रेखा खंडों से बनी होती हैं। इस प्रकार, बहुभुज के रेखाखंडों को भुजाएँ या किनारे कहा जाता है। वह बिंदु जहाँ दो रेखाखंड मिलते हैं उसे शीर्ष या कोने कहा जाता है, इसलिए एक कोण बनता है। बहुभुज का एक उदाहरण तीन भुजाओं वाला त्रिभुज है। वृत्त भी एक समतल आकृति है लेकिन इसे बहुभुज नहीं माना जाता है, क्योंकि यह एक घुमावदार आकृति है और इसमें भुजाएँ या कोण नहीं होते हैं। इसलिए, हम कह सकते हैं कि सभी बहुभुज आकार हैं लेकिन सभी द्वि-आयामी आकृतियाँ बहुभुज नहीं हैं।
बहुभुज क्या होते हैं?
बहुभुज एक बंद आकृति है जो द्वि-आयामी समतल में रेखाखंडों (वक्रों से नहीं) से बनी होती है। बहुभुज दो शब्दों का संयोजन है, यानी पॉली (जिसका अर्थ है कई) और गोन (जिसका अर्थ है भुजाएँ)।
एक बंद आकृति बनाने के लिए, सिरे से सिरे तक जुड़ने के लिए कम से कम तीन रेखा खंडों की आवश्यकता होती है। इस प्रकार न्यूनतम तीन भुजाओं वाले बहुभुज को त्रिभुज के रूप में जाना जाता है और इसे 3-भुज भी कहा जाता है। एक पक्षीय बहुभुज को भुज कहा जाता है।
बहुभुज आकृति
परिभाषा के अनुसार, हम जानते हैं कि बहुभुज रेखाखंडों से बना होता है। नीचे कुछ बहुभुजों की आकृतियाँ दी गई हैं जो विभिन्न संख्या में रेखाखंडों से घिरी हुई हैं।
बहुभुज के गुणधर्म
बहुभुजों के गुण उनकी भुजाओं और कोणों पर आधारित होते हैं।
• एक भुजा वाले बहुभुज के सभी आंतरिक कोणों का योग होता है .
• भुजाओं वाले बहुभुज में विकर्णों की संख्या =
• किसी बहुभुज के एक कोने से विकर्णों को मिलाने पर बनने वाले त्रिभुजों की संख्या =
• भुजा वाले नियमित बहुभुज के प्रत्येक आंतरिक कोण का माप =
• एक भुजा वाले नियमित बहुभुज के प्रत्येक बाह्य कोण का माप=
बहुभुज के प्रकार
भुजाओं और कोणों के आधार पर , बहुभुजों को निम्नलिखित प्रकारों में वर्गीकृत किया जाता है :
- नियमित बहुभुज
- अनियमित बहुभुज
- उत्तल बहुभुज
- अवतल बहुभुज
नियमित बहुभुज
यदि बहुभुज की सभी भुजाएँ और आंतरिक कोण बराबर हों , तो इसे नियमित बहुभुज के रूप में जाना जाता है ।
उदाहरण : वर्ग, समबाहु त्रिभुज आदि ।
अनियमित बहुभुज
यदि किसी बहुभुज की सभी भुजाएँ और आंतरिक कोण अलग-अलग माप के हों, तो उसे अनियमित बहुभुज कहते हैं। इसका मतलब है कि या तो भुजाएँ अलग-अलग लंबाई की हैं या कोण अलग-अलग हैं, जो कि बहुभुज को अनियमित कहने के लिए पर्याप्त है। उदाहरण के लिए, एक विषमबाहु त्रिभुज, एक आयत, एक पतंग, आदि।
उत्तल बहुभुज
यदि किसी बहुभुज के सभी आंतरिक कोण से कम हैं, तो उसे उत्तल बहुभुज के रूप में जाना जाता है। शीर्ष आकृति के केंद्र से बाहर की ओर इंगित करता है।
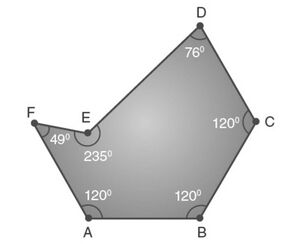
अवतल बहुभुज
यदि किसी बहुभुज के एक या अधिक आंतरिक कोण से अधिक हैं, तो उसे अवतल बहुभुज के रूप में जाना जाता है। एक अवतल बहुभुज में कम से कम चार भुजाएँ हो सकती हैं। शीर्ष बहुभुज के भीतर की ओर इंगित करता है।