वेग में परिवर्तन की दर: Difference between revisions
Listen
| (One intermediate revision by the same user not shown) | |||
| Line 9: | Line 9: | ||
====== गणितीय समीकरण ====== | ====== गणितीय समीकरण ====== | ||
त्वरण का वर्णन करने वाला गणितीय समीकरण है: | त्वरण का वर्णन करने वाला गणितीय समीकरण है: | ||
<math>Acceleration(a)=\frac{Change\;in\;Velocity(\Delta v)}{Time(\Delta t)},</math> | <math>Acceleration(a)=\frac{Change\;in\;Velocity(\Delta v)}{Time(\Delta t)},</math> | ||
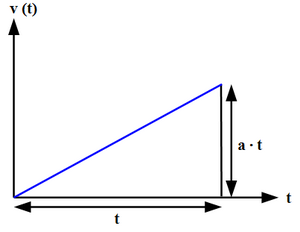
[[File:Strecke und konstante Beschleunigung.png|thumb|एकसमान त्वरण के लिए गति अंतर की गणना ]] | [[File:Strecke und konstante Beschleunigung.png|thumb|एकसमान त्वरण के लिए गति अंतर की गणना ]] | ||
<math>a</math> वस्तु के त्वरण को दर्शाता है (मीटर प्रति सेकंड वर्ग, <math>m/s^2</math> में) | <math>a</math> वस्तु के त्वरण को दर्शाता है (मीटर प्रति सेकंड वर्ग, <math>m/s^2</math> में) (चित्र में <math>a </math> से दर्शाया गया है ) | ||
<math>\Delta v</math> वेग में परिवर्तन (मीटर प्रति सेकंड, <math>m/s</math> में) का प्रतिनिधित्व करता है (चित्र में <math>v(t)</math> | <math>\Delta v</math> वेग में परिवर्तन (मीटर प्रति सेकंड, <math>m/s</math> में) का प्रतिनिधित्व करता है (चित्र में <math>v(t)</math> द्वारा दर्शाया गया है ) | ||
<math>\Delta t</math> समय में परिवर्तन (सेकंड में, <math>s</math>) का प्रतिनिधित्व करता | <math>\Delta t</math> समय में परिवर्तन (सेकंड में, <math>s</math>) का प्रतिनिधित्व करता है (चित्र में <math>t</math> से दर्शाया गया है ) | ||
====== सदिश के रूप में त्वरण ====== | ====== सदिश के रूप में त्वरण ====== | ||
| Line 26: | Line 26: | ||
====== सकारात्मक त्वरण ====== | ====== सकारात्मक त्वरण ====== | ||
जब किसी वस्तु का वेग बढ़ता है (चाहे परिमाण, दिशा या दोनों | जब किसी वस्तु का वेग बढ़ता है (चाहे परिमाण के माप के रूप में अथवा, दिशा के बदलाव के कारण या दोनों ही कारकों के कारण ), तो यह सकारात्मक त्वरण का अनुभव करता है। इसका तात्पर्य यह है कि इस वस्तु की गति में न सिर्फ बदलाव आ रहा है बल्कि उसके वेग के परिवर्तन में शीघ्रता आ रही है। | ||
====== नकारात्मक त्वरण (मंदी) ====== | ====== नकारात्मक त्वरण (मंदी) ====== | ||
जब किसी वस्तु का वेग कम हो जाता है (चाहे परिमाण, दिशा या दोनों में), तो यह नकारात्मक त्वरण का अनुभव करता है, जिसे अक्सर मंदी कहा जाता है। इसका मतलब यह धीमा हो रहा | जब किसी वस्तु का वेग कम हो जाता है (चाहे परिमाण, दिशा या दोनों में), तो यह नकारात्मक त्वरण का अनुभव करता है, जिसे अक्सर मंदी कहा जाता है। इसका मतलब यह धीमा हो रहा है। | ||
====== शून्य त्वरण ====== | ====== शून्य त्वरण ====== | ||
Latest revision as of 13:06, 28 November 2023
Rate of change of Velocity
त्वरण, वेग में परिवर्तन की दर है। यह इस तथ्य का माप है कि किसी चलायमान वस्तु का वेग समय के साथ, कितनी शीघ्रता से बदल रहा है। गणना अथवा अन्य प्रकार के मापन में त्वरण का माप ,दो चरों, गति (परिमाण) और दिशा के परिवर्तन पर निर्भर करता है।
मुख्य बिंदु
गणितीय समीकरण
त्वरण का वर्णन करने वाला गणितीय समीकरण है:
वस्तु के त्वरण को दर्शाता है (मीटर प्रति सेकंड वर्ग, में) (चित्र में से दर्शाया गया है )
वेग में परिवर्तन (मीटर प्रति सेकंड, में) का प्रतिनिधित्व करता है (चित्र में द्वारा दर्शाया गया है )
समय में परिवर्तन (सेकंड में, ) का प्रतिनिधित्व करता है (चित्र में से दर्शाया गया है )
सदिश के रूप में त्वरण
वेग की तरह, त्वरण भी एक सदिश (वेक्टर)राशि है। इसमें परिमाण (किसी वस्तु का वेग ,कितनी शीघ्रता से घट अथवा बढ रहा है) और दिशा (यह बदलाव किस दिशा में हो रहा है) दोनों ही अंतर्निहित हैं। त्वरण का सदिश-रूप ,वेग बी बदलती दिशा को इंगित करता है और इसस प्रकार वेग में हो रहे बदलाव को गणना योग्य दर्शाने में सहायक है।
इकाइयाँ
अंतर्राष्ट्रीय इकाइयों की प्रणाली (SI) में, त्वरण को मीटर प्रति सेकंड वर्ग (m/s²) में मापा जाता है।
सकारात्मक त्वरण
जब किसी वस्तु का वेग बढ़ता है (चाहे परिमाण के माप के रूप में अथवा, दिशा के बदलाव के कारण या दोनों ही कारकों के कारण ), तो यह सकारात्मक त्वरण का अनुभव करता है। इसका तात्पर्य यह है कि इस वस्तु की गति में न सिर्फ बदलाव आ रहा है बल्कि उसके वेग के परिवर्तन में शीघ्रता आ रही है।
नकारात्मक त्वरण (मंदी)
जब किसी वस्तु का वेग कम हो जाता है (चाहे परिमाण, दिशा या दोनों में), तो यह नकारात्मक त्वरण का अनुभव करता है, जिसे अक्सर मंदी कहा जाता है। इसका मतलब यह धीमा हो रहा है।
शून्य त्वरण
यदि किसी वस्तु का वेग स्थिर रहता है (न तो तेज और न ही धीमा), तो उसका त्वरण शून्य होता है।
संक्षेप में
त्वरण को समझना महत्वपूर्ण है क्योंकि इससे हमें यह समझाने में मदद मिलती है कि किसी वस्तु की गति समय के साथ कैसे बदलती है। यह भौतिकी में एक मौलिक भूमिका निभाता है और यांत्रिकी के विभिन्न पहलुओं और गति में वस्तुओं के व्यवहार को समझने के लिए आवश्यक है।