बारंबारता बहुभुज: Difference between revisions
No edit summary |
Ramamurthy (talk | contribs) No edit summary |
||
| (10 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
[[File:Frequency Polygon - Hindi.jpg|thumb|चित्र-1आयतचित्र | | बारंबारता बहुभुज को एक आलेख के रूप में परिभाषित किया जा सकता है जो सांख्यिकी में व्यापक रूप से उपयोग की जाने वाली जानकारी या आंकड़ों की व्याख्या करता है। आंकड़ों के निरूपण का यह दृश्य, रूप, आंकड़ों के आकार, और प्रवृत्ति को संगठित और व्यवस्थित तरीके से चित्रित करने में सहायता करता है। आलेख के आकार के माध्यम से बारंबारता बहुभुज, वर्ग अंतराल की घटना की संख्या को दर्शाते हैं। इस प्रकार का आलेख प्रायः आयतचित्र(हिस्टोग्राम) के साथ खींचा जाता है, लेकिन आयतचित्र के बिना भी खींचा जा सकता है। जबकि आयतचित्र बिना रिक्त स्थान के आयताकार दंडों वाला एक आलेख होता है, बारंबारता बहुभुज आलेख एक रेखा आलेख होता है जो संचयी बारंबारता बंटन आंकड़ों का निरूपण करता है। | ||
[[File:Frequency Polygon - Without Histogram - Hindi.jpg|thumb|चित्र -1आयतचित्र के साथ बारंबारता बहुभुज]] | '''उदाहरण''': एक कक्षा में 28 छात्रों के वजन की बारंबारता का वर्णन करने वाली निम्नलिखित बारंबारता बंटन तालिका के लिए आयतचित्र का निर्माण करके एक बारंबारता बहुभुज का निर्माण करें। | ||
{| class="wikitable" | |||
!वज़न (किलो में) | |||
!छात्रों की संख्या | |||
|- | |||
|30.5 - 35.5 | |||
|8 | |||
|- | |||
|35.5 - 40.5 | |||
|10 | |||
|- | |||
|40.5 - 45.5 | |||
|4 | |||
|- | |||
|45.5 - 50.5 | |||
|2 | |||
|- | |||
|50.5 - 55.5 | |||
|4 | |||
|- | |||
| '''कुल''' | |||
|'''28''' | |||
|}आइए ऊपर दिए गए आंकड़ों को निम्न प्रकार से आलेखीय रूप से प्रस्तुत करें: | |||
आयतचित्र(हिस्टोग्राम) निर्माण: | |||
(i) हम क्षैतिज अक्ष पर वजन/भारों को उपयुक्त पैमाने पर निरूपित करते हैं। हम पैमाना 1 सेमी = 5 किग्रा के रूप में चुन सकते हैं। साथ ही, चूँकि प्रथम वर्ग अंतराल 30.5 से प्रारंभ होता है न कि शून्य से, हम इसे अक्ष पर एक विराम चिह्नित करके आलेख पर दिखाते हैं। | |||
(ii) हम उपयुक्त पैमाने पर ऊर्ध्वाधर अक्ष पर छात्रों की संख्या (बारंबारता ) का निरूपण करते हैं। चूँकि अधिकतम बारंबारता 10 है, हमें इस अधिकतम बारंबारता को समायोजित करने के लिए पैमाना चुनने की आवश्यकता है। | |||
(iii) अब हम वर्ग-आकार के समान चौड़ाई और संगत वर्ग अंतराल की आवृत्तियों के अनुसार लंबाई वाले आयत (या आयताकार दंड) बनाते हैं। उदाहरण के लिए, वर्ग अंतराल 30.5 - 35.5 के लिए आयत की चौड़ाई 1 सेमी और लंबाई 4 सेमी होगी। | |||
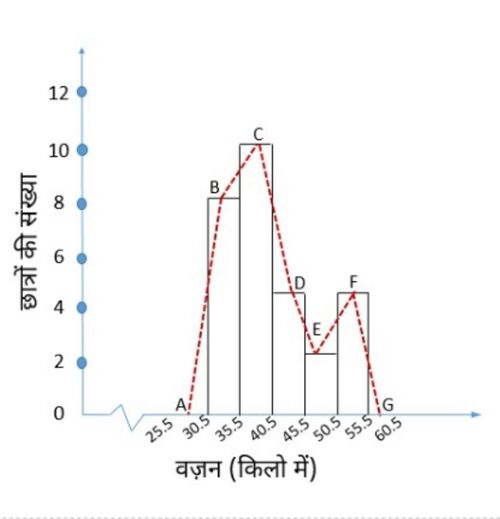
(iv) इस तरह, हमने हिस्टोग्राम का निर्माण किया[[File:Frequency Polygon - Hindi.jpg|thumb|चित्र-1आयतचित्र |none|519x519px]] | |||
आइए इस आयतचित्र(हिस्टोग्राम) के आसन्न आयतों की ऊपरी भुजाओं के मध्य-बिंदुओं को रेखाखंडों के माध्यम से जोड़ें। आइए हम इन मध्य-बिंदुओं को B, C, D, E, F और G कहें। जब रेखाखंडों से जोड़ा जाता है, तो हमें आकृति BCDEF प्राप्त होती है (चित्र-1 देखें)। बहुभुज को पूरा करने के लिए, हम मानते हैं कि 30.5 - 35.5 से पहले शून्य बारंबारता वाला एक वर्ग अंतराल है, और 50.5 - 55.5 के बाद एक है, और उनके मध्य-बिंदु क्रमशः A और G हैं। ABCDEFG चित्र 1 में दिखाए गए आंकड़ों के अनुरूप बारंबारता बहुभुज है। | |||
बारंबारता बहुभुज को बिना आयतचित्र खींचे स्वतंत्र रूप से भी खींचा जा सकता है। इसके लिए, हमें आंकड़ों में प्रयुक्त वर्ग अंतराल के मध्य-बिंदुओं की आवश्यकता होती है। वर्ग अंतराल के इन मध्य बिंदुओं को वर्ग चिह्न कहा जाता है। | |||
किसी वर्ग अंतराल का वर्ग चिह्न ज्ञात करने के लिए, हम किसी वर्ग की ऊपरि सीमा और निम्न सीमा का योग ज्ञात करते हैं और उसे 2 से विभाजित करते हैं। | |||
इस प्रकार, वर्ग-चिह्न = (ऊपरि सीमा + निम्न सीमा) / 2 | |||
'''उदाहरण''': निम्नलिखित बारंबारता बंटन सारणी के लिए हिस्टोग्राम बनाए बिना एक आयतचित्र बहुभुज का निर्माण कीजिए जो एक कक्षा में 28 छात्रों द्वारा प्राप्त अंकों की बारंबारता का वर्णन करता है। | |||
{| class="wikitable" | |||
!अंक | |||
!छात्रों की संख्या | |||
|- | |||
|140 - 150 | |||
|8 | |||
|- | |||
|150 - 160 | |||
|10 | |||
|- | |||
|160 - 170 | |||
|4 | |||
|- | |||
|170 - 180 | |||
|2 | |||
|- | |||
|180 - 190 | |||
|4 | |||
|- | |||
|'''कुल''' | |||
|'''28''' | |||
|} | |||
'''हल''' : चूँकि हम हिस्टोग्राम के बिना एक बारंबारता बहुभुज बनाना चाहते हैं, तो आइए ऊपर दिए गए वर्गों के वर्ग-चिह्न ज्ञात करें, अर्थात 140 - 150, 150 - 160,.... | |||
140 - 150 के लिए, ऊपरि सीमा = 150, और निम्न सीमा = 140 | |||
वर्ग-चिह्न = (ऊपरि सीमा + निम्न सीमा) / 2 | |||
तो, वर्ग-चिह्न =<math>\frac{150+140}{2}=\frac{290}{2}=145</math> | |||
इसी तरह आगे बढ़ते हुए, हम अन्य वर्गों के वर्ग चिह्न भी ज्ञात करते हैं। | |||
तो, प्राप्त नई तालिका निम्न तालिका में दर्शाई गई है: | |||
{| class="wikitable" | |||
!कक्षा | |||
!वर्ग-चिह्न | |||
!बारंबारता | |||
|- | |||
|140 - 150 | |||
|145 | |||
|8 | |||
|- | |||
|150 - 160 | |||
|155 | |||
|10 | |||
|- | |||
|160 - 170 | |||
| 165 | |||
|4 | |||
|- | |||
|170 - 180 | |||
|175 | |||
|2 | |||
|- | |||
|180 - 190 | |||
|185 | |||
|4 | |||
|- | |||
|'''कुल''' | |||
| | |||
|'''28''' | |||
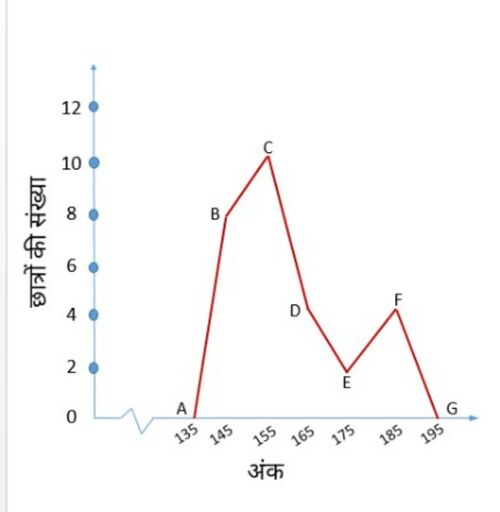
|}[[File:Frequency Polygon - Without Histogram - Hindi.jpg|thumb|चित्र -1आयतचित्र के साथ बारंबारता बहुभुज|none|512x512px]]अब हम क्षैतिज अक्ष के साथ वर्ग-चिह्नों और ऊर्ध्वाधर-अक्ष के साथ बारंबारता को आलेखित करके और फिर बिंदुओं B(145, 8), C(155, 10), D( 165, 4), E(175, 2) और F(185, 4) को रेखाखंडों द्वारा आलेखित करके और जोड़कर एक बारंबारता बहुभुज बना सकते हैं। हमें शून्य बारंबारता वाले वर्ग 130 - 140 (निम्नतम वर्ग 140 - 150 से ठीक पहले) के वर्ग-चिह्न के अनुरूप बिंदु, यानी A (135, 0), और बिंदु G(195 , 0), F(185, 4) के तुरंत बाद होता है, को आलेखित करना नहीं भूलना चाहिए। तो, परिणामी बारंबारता बहुभुज ABCDEFG होगा (चित्र-2 देखें)। | |||
बारंबारता बहुभुज का उपयोग तब किया जाता है जब आंकडें अखंड और बहुत बड़े होते हैं। यह एक ही प्रकृति के दो अलग-अलग आंकड़ों के समुच्चयों की तुलना करने के लिए बहुत उपयोगी है, उदाहरण के लिए, एक ही वर्ग के दो अलग-अलग वर्गों के निरूपण की तुलना करना। | |||
[[Category:सांख्यिकी]] | |||
[[Category:कक्षा-9]] | |||
[[Category:गणित]] | |||
Latest revision as of 06:32, 19 June 2024
बारंबारता बहुभुज को एक आलेख के रूप में परिभाषित किया जा सकता है जो सांख्यिकी में व्यापक रूप से उपयोग की जाने वाली जानकारी या आंकड़ों की व्याख्या करता है। आंकड़ों के निरूपण का यह दृश्य, रूप, आंकड़ों के आकार, और प्रवृत्ति को संगठित और व्यवस्थित तरीके से चित्रित करने में सहायता करता है। आलेख के आकार के माध्यम से बारंबारता बहुभुज, वर्ग अंतराल की घटना की संख्या को दर्शाते हैं। इस प्रकार का आलेख प्रायः आयतचित्र(हिस्टोग्राम) के साथ खींचा जाता है, लेकिन आयतचित्र के बिना भी खींचा जा सकता है। जबकि आयतचित्र बिना रिक्त स्थान के आयताकार दंडों वाला एक आलेख होता है, बारंबारता बहुभुज आलेख एक रेखा आलेख होता है जो संचयी बारंबारता बंटन आंकड़ों का निरूपण करता है।
उदाहरण: एक कक्षा में 28 छात्रों के वजन की बारंबारता का वर्णन करने वाली निम्नलिखित बारंबारता बंटन तालिका के लिए आयतचित्र का निर्माण करके एक बारंबारता बहुभुज का निर्माण करें।
| वज़न (किलो में) | छात्रों की संख्या |
|---|---|
| 30.5 - 35.5 | 8 |
| 35.5 - 40.5 | 10 |
| 40.5 - 45.5 | 4 |
| 45.5 - 50.5 | 2 |
| 50.5 - 55.5 | 4 |
| कुल | 28 |
आइए ऊपर दिए गए आंकड़ों को निम्न प्रकार से आलेखीय रूप से प्रस्तुत करें:
आयतचित्र(हिस्टोग्राम) निर्माण:
(i) हम क्षैतिज अक्ष पर वजन/भारों को उपयुक्त पैमाने पर निरूपित करते हैं। हम पैमाना 1 सेमी = 5 किग्रा के रूप में चुन सकते हैं। साथ ही, चूँकि प्रथम वर्ग अंतराल 30.5 से प्रारंभ होता है न कि शून्य से, हम इसे अक्ष पर एक विराम चिह्नित करके आलेख पर दिखाते हैं।
(ii) हम उपयुक्त पैमाने पर ऊर्ध्वाधर अक्ष पर छात्रों की संख्या (बारंबारता ) का निरूपण करते हैं। चूँकि अधिकतम बारंबारता 10 है, हमें इस अधिकतम बारंबारता को समायोजित करने के लिए पैमाना चुनने की आवश्यकता है।
(iii) अब हम वर्ग-आकार के समान चौड़ाई और संगत वर्ग अंतराल की आवृत्तियों के अनुसार लंबाई वाले आयत (या आयताकार दंड) बनाते हैं। उदाहरण के लिए, वर्ग अंतराल 30.5 - 35.5 के लिए आयत की चौड़ाई 1 सेमी और लंबाई 4 सेमी होगी।
(iv) इस तरह, हमने हिस्टोग्राम का निर्माण किया
आइए इस आयतचित्र(हिस्टोग्राम) के आसन्न आयतों की ऊपरी भुजाओं के मध्य-बिंदुओं को रेखाखंडों के माध्यम से जोड़ें। आइए हम इन मध्य-बिंदुओं को B, C, D, E, F और G कहें। जब रेखाखंडों से जोड़ा जाता है, तो हमें आकृति BCDEF प्राप्त होती है (चित्र-1 देखें)। बहुभुज को पूरा करने के लिए, हम मानते हैं कि 30.5 - 35.5 से पहले शून्य बारंबारता वाला एक वर्ग अंतराल है, और 50.5 - 55.5 के बाद एक है, और उनके मध्य-बिंदु क्रमशः A और G हैं। ABCDEFG चित्र 1 में दिखाए गए आंकड़ों के अनुरूप बारंबारता बहुभुज है।
बारंबारता बहुभुज को बिना आयतचित्र खींचे स्वतंत्र रूप से भी खींचा जा सकता है। इसके लिए, हमें आंकड़ों में प्रयुक्त वर्ग अंतराल के मध्य-बिंदुओं की आवश्यकता होती है। वर्ग अंतराल के इन मध्य बिंदुओं को वर्ग चिह्न कहा जाता है।
किसी वर्ग अंतराल का वर्ग चिह्न ज्ञात करने के लिए, हम किसी वर्ग की ऊपरि सीमा और निम्न सीमा का योग ज्ञात करते हैं और उसे 2 से विभाजित करते हैं।
इस प्रकार, वर्ग-चिह्न = (ऊपरि सीमा + निम्न सीमा) / 2
उदाहरण: निम्नलिखित बारंबारता बंटन सारणी के लिए हिस्टोग्राम बनाए बिना एक आयतचित्र बहुभुज का निर्माण कीजिए जो एक कक्षा में 28 छात्रों द्वारा प्राप्त अंकों की बारंबारता का वर्णन करता है।
| अंक | छात्रों की संख्या |
|---|---|
| 140 - 150 | 8 |
| 150 - 160 | 10 |
| 160 - 170 | 4 |
| 170 - 180 | 2 |
| 180 - 190 | 4 |
| कुल | 28 |
हल : चूँकि हम हिस्टोग्राम के बिना एक बारंबारता बहुभुज बनाना चाहते हैं, तो आइए ऊपर दिए गए वर्गों के वर्ग-चिह्न ज्ञात करें, अर्थात 140 - 150, 150 - 160,....
140 - 150 के लिए, ऊपरि सीमा = 150, और निम्न सीमा = 140
वर्ग-चिह्न = (ऊपरि सीमा + निम्न सीमा) / 2
तो, वर्ग-चिह्न =
इसी तरह आगे बढ़ते हुए, हम अन्य वर्गों के वर्ग चिह्न भी ज्ञात करते हैं।
तो, प्राप्त नई तालिका निम्न तालिका में दर्शाई गई है:
| कक्षा | वर्ग-चिह्न | बारंबारता |
|---|---|---|
| 140 - 150 | 145 | 8 |
| 150 - 160 | 155 | 10 |
| 160 - 170 | 165 | 4 |
| 170 - 180 | 175 | 2 |
| 180 - 190 | 185 | 4 |
| कुल | 28 |
अब हम क्षैतिज अक्ष के साथ वर्ग-चिह्नों और ऊर्ध्वाधर-अक्ष के साथ बारंबारता को आलेखित करके और फिर बिंदुओं B(145, 8), C(155, 10), D( 165, 4), E(175, 2) और F(185, 4) को रेखाखंडों द्वारा आलेखित करके और जोड़कर एक बारंबारता बहुभुज बना सकते हैं। हमें शून्य बारंबारता वाले वर्ग 130 - 140 (निम्नतम वर्ग 140 - 150 से ठीक पहले) के वर्ग-चिह्न के अनुरूप बिंदु, यानी A (135, 0), और बिंदु G(195 , 0), F(185, 4) के तुरंत बाद होता है, को आलेखित करना नहीं भूलना चाहिए। तो, परिणामी बारंबारता बहुभुज ABCDEFG होगा (चित्र-2 देखें)।
बारंबारता बहुभुज का उपयोग तब किया जाता है जब आंकडें अखंड और बहुत बड़े होते हैं। यह एक ही प्रकृति के दो अलग-अलग आंकड़ों के समुच्चयों की तुलना करने के लिए बहुत उपयोगी है, उदाहरण के लिए, एक ही वर्ग के दो अलग-अलग वर्गों के निरूपण की तुलना करना।