किरचॉफ के नियम: Difference between revisions
Listen
| (10 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
Kirchoff's Law | Kirchoff's Law | ||
किरचॉफ के नियम सर्किट विश्लेषण में मौलिक सिद्धांत हैं,जो यह समझने में सुविधा करते हैं कि विद्युत परिपथ (सर्किट) में धाराएं और वोल्टेज कैसे व्यवहार करते हैं। | किरचॉफ के नियम, सर्किट विश्लेषण में मौलिक सिद्धांत हैं,जो यह समझने में सुविधा करते हैं कि विद्युत परिपथ (सर्किट) में धाराएं और वोल्टेज कैसे व्यवहार करते हैं। | ||
== किरचॉफ के दोनों नियमों की व्याख्या: == | == किरचॉफ के दोनों नियमों की व्याख्या: == | ||
== | विद्युत अभियांत्रिकी में,लघुतम,मध्यम अथवा उच्चतम श्रेणी की जटिलता लीये सर्किट परिपथ में उपस्थित सक्रीय और निष्क्रीय अवयव तत्वों के ऊर्जित अवस्था के विश्लेषण व संशलेषण करने में विद्युतीय प्रवाह व विभव अंतर के ज्ञान का महत्वपूर्ण स्थान है। ऐसे में किरचॉफ के दोनों नियमों ,एक धारा संबंधित व दूसरा विभव अंतर संबंधित, आचरण की समझ बढ़ाने में,मूलभूत योगदान देते हैं। | ||
यह नियम, जिसे किरचॉफ का पहला नियम या किरचॉफ का जंक्शन नियम भी कहा जाता है, कहता है कि, विद्युत परिपथ में किसी भी | |||
यहाँ उन दोनों नियमों का विश्लेषण कीया गया है। | |||
== किरचॉफ का विद्युतीय प्रवाह संबंधित नियम (KCL के सी एल ) == | |||
यह नियम, जिसे किरचॉफ का पहला नियम या किरचॉफ का संधिस्थल (नोड जंक्शन) नियम भी कहा जाता है, कहता है कि, विद्युत परिपथ में किसी भी संधिस्थल के लिए, उस नोड में बहने वाली धाराओं का योग, उस नोड से बहने वाली धाराओं के योग के समतुल्य होता है। | |||
===== केसीएल का कथन ===== | |||
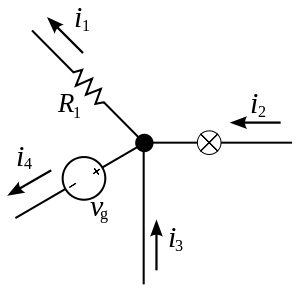
[[File:KCL - Kirchhoff's circuit laws.svg|thumb|किसी भी संधिस्थल (जंक्शन) में प्रवेश करने वाली धारा उस संधिस्थल से निकलने वाली धारा के समतुल्य होती है। i2+ i3 = i1+i4]] | [[File:KCL - Kirchhoff's circuit laws.svg|thumb|किसी भी संधिस्थल (जंक्शन) में प्रवेश करने वाली धारा उस संधिस्थल से निकलने वाली धारा के समतुल्य होती है। i2+ i3 = i1+i4]] | ||
एक बिंदु पर मिलने वाले चालकों (कंडक्टरों) के संजाल (नेटवर्क) में धाराओं का बीजगणितीय योग शून्य है। | एक बिंदु पर मिलने वाले चालकों (कंडक्टरों) के संजाल (नेटवर्क) में धाराओं का बीजगणितीय योग शून्य है। | ||
यह याद करते हुए, कि विद्युतीय प्रवाह, सकारात्मक (या नकारात्मक) सांकेतिक मात्रा है जो किसी नोड की ओर या उससे दूर दिशा को दर्शाती है, इस सिद्धांत को संक्षेप में, इस प्रकार भी उद्धृत कीया जा सकता है: | ===== गणितीय समीकरण ===== | ||
यह याद करते हुए, कि विद्युतीय प्रवाह, सकारात्मक (या नकारात्मक) सांकेतिक मात्रा है, जो किसी नोड की ओर या उससे दूर दिशा को दर्शाती है, इस सिद्धांत को संक्षेप में, इस प्रकार भी उद्धृत कीया जा सकता है: | |||
<math> \sum_{i=1}^n I_i = 0</math> | <math> \sum_{i=1}^n I_i = 0</math> | ||
| Line 19: | Line 26: | ||
<math>I_{i}</math>: नोड में प्रवाहित होने वाली धारा। | <math>I_{i}</math>: नोड में प्रवाहित होने वाली धारा। | ||
===== समकक्ष कथन : आवेश का संरक्षण ===== | |||
किरचॉफ का विद्युतीय प्रवाह संबंधित नियम, विद्युत परिपथ में एक आसंधि (नोड) पर विद्युत आवेश के संरक्षण के बारे में है। विद्युतीय आसंधि , एक ऐसा बिंदु है, जहां दो या दो से अधिक परिपथ तत्व, जैसे प्रतिरोधक या तार, जुड़े होते हैं। | किरचॉफ का विद्युतीय प्रवाह संबंधित नियम, विद्युत परिपथ में एक आसंधि (नोड) पर विद्युत आवेश के संरक्षण के बारे में है। विद्युतीय आसंधि , एक ऐसा बिंदु है, जहां दो या दो से अधिक परिपथ तत्व, जैसे प्रतिरोधक या तार, जुड़े होते हैं। | ||
यह सिद्धांत सुनिश्चित करता है कि,एक नोड पर, विद्युत आवेश संरक्षित रहता है ; जितनी भी मात्रा का चार्ज नोड में प्रवाहित होता है, वह उससे बाहर निकलना चाहिए। | यह सिद्धांत सुनिश्चित करता है कि,एक नोड पर, विद्युत आवेश संरक्षित रहता है ; व्यवहारिक दृष्टि से, जितनी भी मात्रा का आवेश (चार्ज) नोड में प्रवाहित होता है, वह उससे बाहर निकलना चाहिए। | ||
== किरचॉफ का वोल्टेज नियम (KVL) == | |||
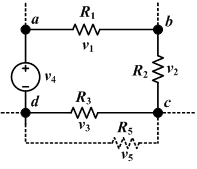
किसी भी विद्युतीय परिपथ बंद में वोल्टेज (संभावित) अंतर का बीजगणितीय योग शून्य के समतुल्य होना चाहिए। (यह नियम, एक बंद सर्किट,पर कारगर है ) चूँकि किसी भी जटिल सर्किट को कई बंद सर्किट में विभाजित किया जा सकता है। | किसी भी विद्युतीय परिपथ बंद में वोल्टेज (संभावित) अंतर का बीजगणितीय योग शून्य के समतुल्य होना चाहिए। (यह नियम, एक बंद सर्किट,पर कारगर है ) चूँकि किसी भी जटिल सर्किट को कई बंद सर्किट में विभाजित किया जा सकता है।[[File:KVL.png|thumb|बंद सर्किट परिपथ (लूप) के चारों ओर, सभी वोल्टेज का योग शून्य के समतुल्य है। v1+v2+v3+v4 = 0]] | ||
===== केवीएल का कथन ===== | |||
किसी सर्किट में किसी भी बंद लूप के चारों ओर वोल्टेज का बीजगणितीय योग शून्य के संबंधित है। | |||
===== गणितीय समीकरण ===== | |||
समीकरण रूप में, KVL को इस प्रकार व्यक्त किया जा सकता है: | |||
<math>\sum_{i=1}^n V_i = 0,</math> | |||
इस समीकरण में: | |||
<math>|\Sigma</math>: एक बंद लूप के चारों ओर वोल्टेज के योग (जोड़ने) का प्रतिनिधित्व करता है। | |||
<math>V_{i}</math>: लूप में प्रत्येक तत्व (वोल्टेज स्रोत और वोल्टेज ड्रॉप) में वोल्टेज। | |||
===== समकक्ष कथन : विभव अंतर से विस्थापित ऊर्जा के संरक्षण संबंधी ===== | |||
इस नियम के विश्लेषण का एक दृष्टिकोण है, यह भी है की ऐसे किसी भी सर्किट परिपथ, की जिसमें न्यूनतम मात्रा के उपकरण जैसे की एक विद्युत सेल और एक विद्युत प्रतिरोध विद्यमान है, में विद्युत सेल आवेश को, एक इलेक्ट्रोमोटिव बल देता है, और फिर विद्युत प्रतिरोध इस बल को नष्ट कर देता है। लेकिन विद्युत प्रतिरोध में यदि दिशा धारा की दिशा के विपरीत है, तो यह विद्युत प्रतिरोध इलेक्ट्रोमोटिव बल में जुड़ जाता है। किरचॉफ का यह दूसरा नियम विद्युतीय विभव के अंतर से उत्पन्न ऊर्जा के संरक्षण नियम पर आधारित है। | |||
किरचॉफ का वोल्टेज नियम विद्युत परिपथ में ऊर्जा के संरक्षण से संबंधित है। इसमें कहा गया है कि एक सर्किट में बंद लूप में इलेक्ट्रोमोटिव बलों (ईएमएफ, जैसे बैटरी या वोल्टेज स्रोत) और वोल्टेज ड्रॉप का कुल योग शून्य के संबंधित है। | |||
यह सिद्धांत सुनिश्चित करता है कि ऊर्जा एक बंद लूप में संरक्षित है; एक लूप में तत्वों के बीच कुल | यह सिद्धांत सुनिश्चित करता है कि ऊर्जा एक बंद लूप में संरक्षित है; एक लूप में तत्वों के बीच कुल विभव अंतर संतुलित होता है।याद रखें कि प्रतिरोधों में वोल्टेज गिरता है (<math>V=I\cdot R,</math>) और बैटरी या अन्य स्रोतों से वोल्टेज बढ़ता है (<math>EMF</math>ईएमएफ) लूप में उनके अभिविन्यास के अनुसार उचित संकेतों के साथ लिया जाना चाहिए। किसी भी बंद लूप के चारों ओर इन वोल्टेज का योग, सर्वथा शून्य होना चाहिए। | ||
ये नियम जटिल विद्युत सर्किट का विश्लेषण करने और सर्किट में विभिन्न बिंदुओं पर धाराओं और वोल्टेज के बीच संबंधों को समझने के लिए अमूल्य उपकरण हैं। | == संक्षेप में == | ||
ये नियम जटिल विद्युत सर्किट का विश्लेषण करने और सर्किट में विभिन्न बिंदुओं पर धाराओं और वोल्टेज के बीच संबंधों को समझने के लिए अमूल्य उपकरण की तरह कारगर है हैं। ये नियम विद्युत सर्किट समस्याओं की एक विस्तृत श्रृंखला को हल करने के लिए संरक्षण के बुनियादी सिद्धांतों को लागू करने की अनुमति देते हैं। | |||
[[Category:विद्युत् धारा]][[Category:कक्षा-12]][[Category:भौतिक विज्ञान]] | [[Category:विद्युत् धारा]][[Category:कक्षा-12]][[Category:भौतिक विज्ञान]] | ||
Latest revision as of 12:31, 31 May 2024
Kirchoff's Law
किरचॉफ के नियम, सर्किट विश्लेषण में मौलिक सिद्धांत हैं,जो यह समझने में सुविधा करते हैं कि विद्युत परिपथ (सर्किट) में धाराएं और वोल्टेज कैसे व्यवहार करते हैं।
किरचॉफ के दोनों नियमों की व्याख्या:
विद्युत अभियांत्रिकी में,लघुतम,मध्यम अथवा उच्चतम श्रेणी की जटिलता लीये सर्किट परिपथ में उपस्थित सक्रीय और निष्क्रीय अवयव तत्वों के ऊर्जित अवस्था के विश्लेषण व संशलेषण करने में विद्युतीय प्रवाह व विभव अंतर के ज्ञान का महत्वपूर्ण स्थान है। ऐसे में किरचॉफ के दोनों नियमों ,एक धारा संबंधित व दूसरा विभव अंतर संबंधित, आचरण की समझ बढ़ाने में,मूलभूत योगदान देते हैं।
यहाँ उन दोनों नियमों का विश्लेषण कीया गया है।
किरचॉफ का विद्युतीय प्रवाह संबंधित नियम (KCL के सी एल )
यह नियम, जिसे किरचॉफ का पहला नियम या किरचॉफ का संधिस्थल (नोड जंक्शन) नियम भी कहा जाता है, कहता है कि, विद्युत परिपथ में किसी भी संधिस्थल के लिए, उस नोड में बहने वाली धाराओं का योग, उस नोड से बहने वाली धाराओं के योग के समतुल्य होता है।
केसीएल का कथन
एक बिंदु पर मिलने वाले चालकों (कंडक्टरों) के संजाल (नेटवर्क) में धाराओं का बीजगणितीय योग शून्य है।
गणितीय समीकरण
यह याद करते हुए, कि विद्युतीय प्रवाह, सकारात्मक (या नकारात्मक) सांकेतिक मात्रा है, जो किसी नोड की ओर या उससे दूर दिशा को दर्शाती है, इस सिद्धांत को संक्षेप में, इस प्रकार भी उद्धृत कीया जा सकता है:
इस समीकरण में:
: धाराओं के योग (जोड़ने) का प्रतिनिधित्व करता है।
: नोड में प्रवाहित होने वाली धारा।
समकक्ष कथन : आवेश का संरक्षण
किरचॉफ का विद्युतीय प्रवाह संबंधित नियम, विद्युत परिपथ में एक आसंधि (नोड) पर विद्युत आवेश के संरक्षण के बारे में है। विद्युतीय आसंधि , एक ऐसा बिंदु है, जहां दो या दो से अधिक परिपथ तत्व, जैसे प्रतिरोधक या तार, जुड़े होते हैं।
यह सिद्धांत सुनिश्चित करता है कि,एक नोड पर, विद्युत आवेश संरक्षित रहता है ; व्यवहारिक दृष्टि से, जितनी भी मात्रा का आवेश (चार्ज) नोड में प्रवाहित होता है, वह उससे बाहर निकलना चाहिए।
किरचॉफ का वोल्टेज नियम (KVL)
किसी भी विद्युतीय परिपथ बंद में वोल्टेज (संभावित) अंतर का बीजगणितीय योग शून्य के समतुल्य होना चाहिए। (यह नियम, एक बंद सर्किट,पर कारगर है ) चूँकि किसी भी जटिल सर्किट को कई बंद सर्किट में विभाजित किया जा सकता है।
केवीएल का कथन
किसी सर्किट में किसी भी बंद लूप के चारों ओर वोल्टेज का बीजगणितीय योग शून्य के संबंधित है।
गणितीय समीकरण
समीकरण रूप में, KVL को इस प्रकार व्यक्त किया जा सकता है:
इस समीकरण में:
: एक बंद लूप के चारों ओर वोल्टेज के योग (जोड़ने) का प्रतिनिधित्व करता है।
: लूप में प्रत्येक तत्व (वोल्टेज स्रोत और वोल्टेज ड्रॉप) में वोल्टेज।
समकक्ष कथन : विभव अंतर से विस्थापित ऊर्जा के संरक्षण संबंधी
इस नियम के विश्लेषण का एक दृष्टिकोण है, यह भी है की ऐसे किसी भी सर्किट परिपथ, की जिसमें न्यूनतम मात्रा के उपकरण जैसे की एक विद्युत सेल और एक विद्युत प्रतिरोध विद्यमान है, में विद्युत सेल आवेश को, एक इलेक्ट्रोमोटिव बल देता है, और फिर विद्युत प्रतिरोध इस बल को नष्ट कर देता है। लेकिन विद्युत प्रतिरोध में यदि दिशा धारा की दिशा के विपरीत है, तो यह विद्युत प्रतिरोध इलेक्ट्रोमोटिव बल में जुड़ जाता है। किरचॉफ का यह दूसरा नियम विद्युतीय विभव के अंतर से उत्पन्न ऊर्जा के संरक्षण नियम पर आधारित है।
किरचॉफ का वोल्टेज नियम विद्युत परिपथ में ऊर्जा के संरक्षण से संबंधित है। इसमें कहा गया है कि एक सर्किट में बंद लूप में इलेक्ट्रोमोटिव बलों (ईएमएफ, जैसे बैटरी या वोल्टेज स्रोत) और वोल्टेज ड्रॉप का कुल योग शून्य के संबंधित है।
यह सिद्धांत सुनिश्चित करता है कि ऊर्जा एक बंद लूप में संरक्षित है; एक लूप में तत्वों के बीच कुल विभव अंतर संतुलित होता है।याद रखें कि प्रतिरोधों में वोल्टेज गिरता है () और बैटरी या अन्य स्रोतों से वोल्टेज बढ़ता है (ईएमएफ) लूप में उनके अभिविन्यास के अनुसार उचित संकेतों के साथ लिया जाना चाहिए। किसी भी बंद लूप के चारों ओर इन वोल्टेज का योग, सर्वथा शून्य होना चाहिए।
संक्षेप में
ये नियम जटिल विद्युत सर्किट का विश्लेषण करने और सर्किट में विभिन्न बिंदुओं पर धाराओं और वोल्टेज के बीच संबंधों को समझने के लिए अमूल्य उपकरण की तरह कारगर है हैं। ये नियम विद्युत सर्किट समस्याओं की एक विस्तृत श्रृंखला को हल करने के लिए संरक्षण के बुनियादी सिद्धांतों को लागू करने की अनुमति देते हैं।