कार्टेशियन पद्धति: Difference between revisions
No edit summary |
Ramamurthy (talk | contribs) No edit summary |
||
| (6 intermediate revisions by one other user not shown) | |||
| Line 6: | Line 6: | ||
जिस पद्धति का उपयोग हम समतल में बिंदुओं को वर्गीकरण करने के लिए करते हैं उसे कार्टेशियन पद्धति के नाम से जाना जाता है। कार्टेशियन रूप संख्या रेखा से प्राप्त होता है। कार्टेशियन निर्देशांक पद्धति को समझने के लिए हमें संख्या रेखा के बारे में अच्छी तरह से जानना चाहिए। इस पद्धति में, हमारे पास निम्नलिखित परिभाषित मापदण्ड हैं जैसे: | जिस पद्धति का उपयोग हम समतल में बिंदुओं को वर्गीकरण करने के लिए करते हैं उसे कार्टेशियन पद्धति के नाम से जाना जाता है। कार्टेशियन रूप संख्या रेखा से प्राप्त होता है। कार्टेशियन निर्देशांक पद्धति को समझने के लिए हमें संख्या रेखा के बारे में अच्छी तरह से जानना चाहिए। इस पद्धति में, हमारे पास निम्नलिखित परिभाषित मापदण्ड हैं जैसे: | ||
दो लंबवत रेखाओं को <math>X</math>-अक्ष <math>(X-X')</math> और <math>Y</math>-अक्ष <math>(Y-Y')</math> नाम दिया गया है। | * दो लंबवत रेखाओं को <math>X</math>-अक्ष <math>(X-X')</math> और <math>Y</math>-अक्ष <math>(Y-Y')</math> नाम दिया गया है। | ||
* इस तल को कार्टेशियन या निर्देशांक तल कहा जाता है और दो रेखाओं <math>(X-X')</math> और <math>(Y-Y')</math> को जब एक साथ रखा जाता है तो उन्हें पद्धति के निर्देशांक अक्ष कहा जाता है। | |||
इस तल को कार्टेशियन या निर्देशांक तल कहा जाता है और दो रेखाओं <math>(X-X')</math> और <math>(Y-Y')</math> को जब एक साथ रखा जाता है तो उन्हें पद्धति के निर्देशांक अक्ष कहा जाता है। | * दो निर्देशांक अक्ष समतल को चार भागों में विभाजित करते हैं जिन्हें चतुर्थाँश कहा जाता है जिन्हें <math>I </math>, <math>II</math>, <math>III </math> और <math>IV </math> वामावर्त से <math>OX</math> कहा जाता है। इसलिए, समतल में अक्ष और ये चतुर्थाँश होते हैं। हम समतल को कार्टेशियन तल या निर्देशांक तल या <math>XY</math>-तल कहते हैं। अक्षों को निर्देशांक अक्ष कहा जाता है। | ||
* अक्षों का प्रतिच्छेदन बिंदु कार्टेशियन प्रणाली का शून्य है। इस बिंदु को सामान्यतः <math>O</math> द्वारा दर्शाया जाएगा। मूल के निर्देशांक को <math>(0,0)</math> के रूप में दर्शाया जाता है। | |||
दो निर्देशांक अक्ष समतल को चार भागों में विभाजित करते हैं जिन्हें | * समतल में किसी भी बिंदु <math>A</math> की स्थिति निर्दिष्ट करने के लिए, हम <math>x</math> की दूरी मापते हैं जिस पर हमें <math>X</math> के साथ चलना है, और फिर <math>y</math> की दूरी मापते हैं जो हमें <math>Y</math> के समानांतर चलना है, ताकि <math>O</math> से <math>A</math> तक पहुँच सकें। दूरियाँ ऋणात्मक हो सकती हैं। | ||
* उदाहरण के लिए, यदि आपको दाईं ओर बढ़ना है, तो <math>x</math> धनात्मक होगा। इसी तरह, यदि आपको <math>Y</math> पर नीचे जाना है, तो <math>y</math> ऋणात्मक होगा। | |||
अक्षों का प्रतिच्छेदन बिंदु कार्टेशियन प्रणाली का शून्य है। इस बिंदु को सामान्यतः <math>O</math> द्वारा दर्शाया जाएगा। मूल के निर्देशांक को <math>(0,0)</math> के रूप में दर्शाया जाता है। | * दो वास्तविक संख्याएँ <math>x</math>और <math>y</math> एक साथ आलेखित करने पर <math>A</math> की स्थिति का विशिष्ट रूप से वर्णन होगा। हम इसे इस प्रकार लिख सकते हैं: <math>A=(2,4)</math> [नीचे चित्र 1 से]। इस प्रकार, <math>A</math> का स्थान दो वास्तविक संख्याओं द्वारा विशिष्ट रूप से वर्गीकृत किया जा सकता है। <math>A</math> के अलग-अलग पदों के लिए <math>A</math>, वास्तविक संख्याओं का यह युग्म भिन्न होगा। | ||
समतल में किसी भी बिंदु <math>A</math> की स्थिति निर्दिष्ट करने के लिए, हम <math>x</math> की दूरी मापते हैं जिस पर हमें <math>X</math> के साथ चलना है, और फिर <math>y</math> की दूरी मापते हैं जो हमें <math>Y</math> के समानांतर चलना है, ताकि <math>O</math> से <math>A</math> तक पहुँच सकें। दूरियाँ ऋणात्मक हो सकती हैं। | |||
उदाहरण के लिए, यदि आपको दाईं ओर बढ़ना है, तो <math>x</math> धनात्मक होगा। इसी तरह, यदि आपको <math>Y</math> पर नीचे जाना है, तो <math>y</math> ऋणात्मक होगा। | |||
दो वास्तविक संख्याएँ <math>x</math>और <math>y</math> एक साथ आलेखित करने पर <math>A</math> की स्थिति का विशिष्ट रूप से वर्णन होगा। हम इसे इस प्रकार लिख सकते हैं: <math>A=(2,4)</math> [नीचे चित्र 1 से]। इस प्रकार, <math>A</math> का स्थान दो वास्तविक संख्याओं द्वारा विशिष्ट रूप से वर्गीकृत किया जा सकता है। <math>A</math> के अलग-अलग पदों के लिए <math>A</math>, वास्तविक संख्याओं का यह युग्म भिन्न होगा। | |||
अब कार्टेशियन निर्देशांक के निम्नलिखित ग्राफिकल निरूपण को देखें और उपरोक्त विवरण को पुनः पढ़ें | अब कार्टेशियन निर्देशांक के निम्नलिखित ग्राफिकल निरूपण को देखें और उपरोक्त विवरण को पुनः पढ़ें | ||
[[File:Cartesian System.jpg| | [[File:Cartesian System - Hindi.jpg|none|thumb|600x600px|चित्र-1कार्टेशियन पद्धति]] | ||
आइए अक्षों से बिंदु <math>A</math> और <math>C</math> की दूरियाँ देखें। हम बिंदु <math>A</math> और <math>C</math> से <math>X</math>-अक्ष और <math>Y</math>-अक्ष पर लंब खींचते हैं। | |||
<math> | बिंदु <math>A</math> का <math>x</math> निर्देशांक <math>Y</math>-अक्ष से बिंदु <math>A</math> की लंबवत दूरी है जो <math>2</math> इकाई है जो धनात्मक है। | ||
<math> | बिंदु <math>A</math> का <math>y</math> निर्देशांक <math>X</math>-अक्ष से बिंदु <math>A</math> की लंबवत दूरी है जो <math>4</math> इकाई है जो धनात्मक है। | ||
<math> | बिंदु <math>C</math> का <math>x</math> निर्देशांक <math>Y</math>-अक्ष से बिंदु <math>C</math> की लंबवत दूरी है जो <math>4</math> इकाई है जो ऋणात्मक है। | ||
<math> | बिंदु <math>C</math> का <math>y</math> निर्देशांक <math>X</math>-अक्ष से बिंदु <math>C</math> की लंबवत दूरी है जो <math>2</math> इकाई है जो ऋणात्मक है। | ||
<math> | <math>x</math> निर्देशांक को भुज भी कहा जाता है। | ||
<math>y</math> निर्देशांक को कोटि भी कहा जाता है। | |||
निर्देशांक तल में किसी बिंदु के निर्देशांक बताने में, <math>x</math>-निर्देशांक पहले आता है, और फिर <math>y</math>-निर्देशांक आता है। हम निर्देशांकों को कोष्ठक में रखते हैं। अतः <math>A</math> के निर्देशांक <math>(2,4)</math> हैं, <math>C</math> के निर्देशांक <math>(-4,-2)</math> हैं। | |||
चूंकि <math>X</math>-अक्ष पर स्थित प्रत्येक बिंदु की <math>X</math>-अक्ष से कोई दूरी (शून्य दूरी) नहीं है, इसलिए, <math>Y</math>-अक्ष पर स्थित प्रत्येक बिंदु का <math>y</math>-निर्देशांक, <math>X</math>-अक्ष सदैव शून्य होता है। इस प्रकार, <math>X</math>- अक्ष पर किसी भी बिंदु के निर्देशांक (<math>x</math>, <math>0</math>) के रूप के होते हैं, जहाँ <math>x</math>, <math>Y</math> - अक्ष से बिंदु की दूरी है। इसी तरह, <math>Y</math> - अक्ष पर किसी भी बिंदु के निर्देशांक (<math>0</math>, <math>y</math>) के रूप के होते हैं, जहाँ <math>y</math> , <math>X</math> - अक्ष से बिंदु की दूरी है। | |||
शून्य दूरी वाले कार्टेशियन निर्देशांक का आलेखीय निरूपण नीचे चित्र-2 में दिखाया गया है। | |||
[[File:Cartesian System with zero -Hindi.jpg|alt=Fig. 2 Cartesian System with zero|none|thumb|600x600px|चित्र. 2 कार्टेशियन पद्धति शून्य के साथ]] | |||
मूल बिन्दु <math>O</math> के निर्देशांक क्या हैं? इसकी दोनों अक्षों से दूरी शून्य है, इसलिए इसका भुज और कोटि दोनों शून्य हैं। इसलिए, मूल बिन्दु के निर्देशांक <math>(0,0)</math> हैं। | |||
Latest revision as of 08:09, 19 June 2024
कार्टेशियन निर्देशांक पद्धति गणित की एक शाखा है जो n-आयामी निर्देशांक तल में किसी बिंदु को विशिष्ट रूप से दर्शाने के तरीके के बारे में बताती है। कार्टेशियन पद्धति का सिद्धांत 17वीं शताब्दी में रेने डेसकार्टेस नामक एक फ्रांसीसी दार्शनिक और गणितज्ञ द्वारा प्रस्तावित किया गया था। इस कार्टेशियन निर्देशांक पद्धति ने यूक्लिडियन ज्यामिति और बीजगणित के बीच संबंध प्रदान किया, जिसने गणित के अध्ययन में क्रांति ला दी है। कार्टेशियन निर्देशांक पद्धति विश्लेषणात्मक ज्यामिति की नींव है और n-आयामी तल में रेखाओं, वक्रों और ज्यामितीय आकृतियों के प्रतिनिधित्व में मदद करती है।
कार्टेशियन पद्धति क्या है?
जिस पद्धति का उपयोग हम समतल में बिंदुओं को वर्गीकरण करने के लिए करते हैं उसे कार्टेशियन पद्धति के नाम से जाना जाता है। कार्टेशियन रूप संख्या रेखा से प्राप्त होता है। कार्टेशियन निर्देशांक पद्धति को समझने के लिए हमें संख्या रेखा के बारे में अच्छी तरह से जानना चाहिए। इस पद्धति में, हमारे पास निम्नलिखित परिभाषित मापदण्ड हैं जैसे:
- दो लंबवत रेखाओं को -अक्ष और -अक्ष नाम दिया गया है।
- इस तल को कार्टेशियन या निर्देशांक तल कहा जाता है और दो रेखाओं और को जब एक साथ रखा जाता है तो उन्हें पद्धति के निर्देशांक अक्ष कहा जाता है।
- दो निर्देशांक अक्ष समतल को चार भागों में विभाजित करते हैं जिन्हें चतुर्थाँश कहा जाता है जिन्हें , , और वामावर्त से कहा जाता है। इसलिए, समतल में अक्ष और ये चतुर्थाँश होते हैं। हम समतल को कार्टेशियन तल या निर्देशांक तल या -तल कहते हैं। अक्षों को निर्देशांक अक्ष कहा जाता है।
- अक्षों का प्रतिच्छेदन बिंदु कार्टेशियन प्रणाली का शून्य है। इस बिंदु को सामान्यतः द्वारा दर्शाया जाएगा। मूल के निर्देशांक को के रूप में दर्शाया जाता है।
- समतल में किसी भी बिंदु की स्थिति निर्दिष्ट करने के लिए, हम की दूरी मापते हैं जिस पर हमें के साथ चलना है, और फिर की दूरी मापते हैं जो हमें के समानांतर चलना है, ताकि से तक पहुँच सकें। दूरियाँ ऋणात्मक हो सकती हैं।
- उदाहरण के लिए, यदि आपको दाईं ओर बढ़ना है, तो धनात्मक होगा। इसी तरह, यदि आपको पर नीचे जाना है, तो ऋणात्मक होगा।
- दो वास्तविक संख्याएँ और एक साथ आलेखित करने पर की स्थिति का विशिष्ट रूप से वर्णन होगा। हम इसे इस प्रकार लिख सकते हैं: [नीचे चित्र 1 से]। इस प्रकार, का स्थान दो वास्तविक संख्याओं द्वारा विशिष्ट रूप से वर्गीकृत किया जा सकता है। के अलग-अलग पदों के लिए , वास्तविक संख्याओं का यह युग्म भिन्न होगा।
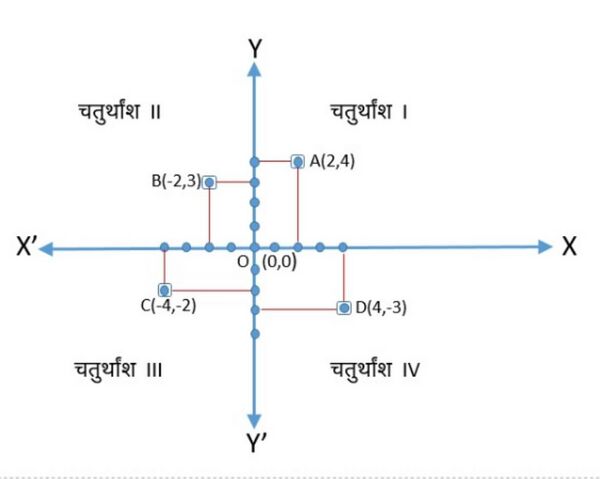
अब कार्टेशियन निर्देशांक के निम्नलिखित ग्राफिकल निरूपण को देखें और उपरोक्त विवरण को पुनः पढ़ें
आइए अक्षों से बिंदु और की दूरियाँ देखें। हम बिंदु और से -अक्ष और -अक्ष पर लंब खींचते हैं।
बिंदु का निर्देशांक -अक्ष से बिंदु की लंबवत दूरी है जो इकाई है जो धनात्मक है।
बिंदु का निर्देशांक -अक्ष से बिंदु की लंबवत दूरी है जो इकाई है जो धनात्मक है।
बिंदु का निर्देशांक -अक्ष से बिंदु की लंबवत दूरी है जो इकाई है जो ऋणात्मक है।
बिंदु का निर्देशांक -अक्ष से बिंदु की लंबवत दूरी है जो इकाई है जो ऋणात्मक है।
निर्देशांक को भुज भी कहा जाता है।
निर्देशांक को कोटि भी कहा जाता है।
निर्देशांक तल में किसी बिंदु के निर्देशांक बताने में, -निर्देशांक पहले आता है, और फिर -निर्देशांक आता है। हम निर्देशांकों को कोष्ठक में रखते हैं। अतः के निर्देशांक हैं, के निर्देशांक हैं।
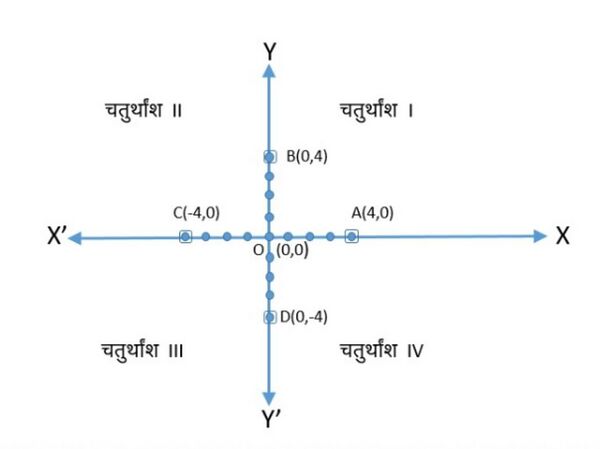
चूंकि -अक्ष पर स्थित प्रत्येक बिंदु की -अक्ष से कोई दूरी (शून्य दूरी) नहीं है, इसलिए, -अक्ष पर स्थित प्रत्येक बिंदु का -निर्देशांक, -अक्ष सदैव शून्य होता है। इस प्रकार, - अक्ष पर किसी भी बिंदु के निर्देशांक (, ) के रूप के होते हैं, जहाँ , - अक्ष से बिंदु की दूरी है। इसी तरह, - अक्ष पर किसी भी बिंदु के निर्देशांक (, ) के रूप के होते हैं, जहाँ , - अक्ष से बिंदु की दूरी है।
शून्य दूरी वाले कार्टेशियन निर्देशांक का आलेखीय निरूपण नीचे चित्र-2 में दिखाया गया है।
मूल बिन्दु के निर्देशांक क्या हैं? इसकी दोनों अक्षों से दूरी शून्य है, इसलिए इसका भुज और कोटि दोनों शून्य हैं। इसलिए, मूल बिन्दु के निर्देशांक हैं।