एक लम्ब वृत्तीय शंकु का पृष्ठीय क्षेत्रफल: Difference between revisions

Latest revision as of 07:13, 11 September 2024

शंकु का पृष्ठीय क्षेत्रफल उसकी सतह द्वारा कवर किया गया कुल क्षेत्रफल है। कुल पृष्ठीय क्षेत्र शंकु के आधार क्षेत्र और पार्श्व पृष्ठीय क्षेत्र को कवर करेगा। शंकु को एक त्रि-आयामी ठोस संरचना के रूप में परिभाषित किया गया है जिसका आधार वृत्तीय है। एक शंकु को गैर-सर्वांगसम वृत्ताकार डिस्क के एक समुच्चय के रूप में देखा जा सकता है जो एक दूसरे के ऊपर इस तरह रखे जाते हैं कि आसन्न डिस्क की त्रिज्या का अनुपात स्थिर रहता है।

चित्र-1 लम्ब वृत्तीय शंकु

चित्र-1 में दर्शाए गए लम्ब वृत्तीय शंकु में शीर्ष पर एक शीर्ष, $r$ आधार त्रिज्या, $h$ शंकु की ऊंचाई तथा $l$ शंकु की तिर्यक ऊंचाई है।

शंकु का वक्र पृष्ठीय क्षेत्रफल = ${\frac {1}{2}}\times l\times 2\pi r=\pi rl$

यहाँ $r$ आधार त्रिज्या, $l$ शंकु की तिर्यक ऊँचाई है।

साथ ही $l^{2}=r^{2}+h^{2}$ पाइथागोरस प्रमेय लागू करने पर। यहाँ $h$ शंकु की ऊँचाई है।

अतः, $l={\sqrt {r^{2}+h^{2}}}$

शंकु का कुल पृष्ठीय क्षेत्रफल = $\pi rl+\pi r^{2}=\pi r(l+r)$

उदाहरण

1. एक लम्ब वृत्तीय शंकु का वक्र पृष्ठीय क्षेत्रफल तथा कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए जिसकी तिर्यक ऊँचाई 10 सेमी तथा आधार त्रिज्या 7 सेमी है।

हल:

वक्र पृष्ठीय क्षेत्रफल = $\pi rl$

= ${\frac {22}{7}}\times 7\times 10=220$ cm²

कुल पृष्ठीय क्षेत्रफल = $\pi r(l+r)$

= ${\frac {22}{7}}\times 7\times (10+7)=374$ cm²

@@ Line 1: / Line 1: @@
-Surface area of a cone is the total area covered by its surface. The total surface area will cover the base area and lateral surface area of the cone. Cone is defined as a three-dimensional solid structure that has a circular base. A cone can be viewed as a set of non-congruent circular disks that are placed over one another such that the ratio of the radius of adjacent disks remains constant.
+शंकु का पृष्ठीय क्षेत्रफल उसकी सतह द्वारा कवर किया गया कुल क्षेत्रफल है। कुल पृष्ठीय क्षेत्र शंकु के आधार क्षेत्र और पार्श्व पृष्ठीय क्षेत्र को कवर करेगा। शंकु को एक त्रि-आयामी ठोस संरचना के रूप में परिभाषित किया गया है जिसका आधार वृत्तीय है। एक शंकु को गैर-सर्वांगसम वृत्ताकार डिस्क के एक समुच्चय के रूप में देखा जा सकता है जो एक दूसरे के ऊपर इस तरह रखे जाते हैं कि आसन्न डिस्क की त्रिज्या का अनुपात स्थिर रहता है।
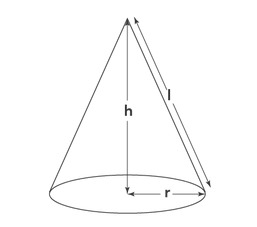
-[[File:Right Circular Cone.jpg|alt=Fig.1 Right Circular Cone|none|thumb|Fig.1 Right Circular Cone]]
+[[File:Right Circular Cone.jpg|alt=Fig.1 Right Circular Cone|none|thumb|चित्र-1 लम्ब वृत्तीय शंकु]]
-Right circular cone shown in Fig. 1 has a vertex at the top, <math>r</math> the base radius , <math>h</math> the height of the cone and <math>l</math> the slant height of the cone.
+चित्र-1 में दर्शाए गए लम्ब वृत्तीय शंकु में शीर्ष पर एक शीर्ष, <math>r</math> आधार त्रिज्या, <math>h</math> शंकु की ऊंचाई तथा <math>l</math> शंकु की तिर्यक ऊंचाई है।
-'''Curved Surface Area of a Cone''' = <math>\frac{1}{2}\times l \times 2\pi r=\pi rl</math>
+'''शंकु का वक्र पृष्ठीय क्षेत्रफल''' = <math>\frac{1}{2}\times l \times 2\pi r=\pi rl</math>
-Here <math>r</math> the base radius , <math>l</math> the slant height of the cone.
+यहाँ <math>r</math> आधार त्रिज्या, <math>l</math> शंकु की तिर्यक ऊँचाई है।
-Also <math>l^2=r^2+h^2</math>  by applying Pythagoras Theorem. Here <math>h</math> is the height of the cone.
+साथ ही  <math>l^2=r^2+h^2</math>  पाइथागोरस प्रमेय लागू करने पर। यहाँ <math>h</math> शंकु की ऊँचाई है।
-Therefore, <math>l=\sqrt{r^2+h^2}</math>
+अतः, <math>l=\sqrt{r^2+h^2}</math>
-'''Total Surface Area of a Cone''' = <math>\pi rl +\pi r^2=\pi r(l+r)
+'''शंकु का कुल पृष्ठीय क्षेत्रफल''' = <math>\pi rl +\pi r^2=\pi r(l+r)
 </math>
-== Examples ==
+== उदाहरण ==
-. Find the curved surface area and the total surface area of a right circular cone whose slant height is <math>10</math> cm and base radius is <math>7</math> cm.
+. एक लम्ब वृत्तीय शंकु का वक्र पृष्ठीय क्षेत्रफल तथा कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए जिसकी तिर्यक ऊँचाई 10 सेमी तथा आधार त्रिज्या 7 सेमी है।
-Solution:
+हल:
-Curved surface area = <math>\pi rl</math>
+वक्र पृष्ठीय क्षेत्रफल = <math>\pi rl</math>
 = <math>\frac{22}{7}\times 7 \times 10= 220</math> cm<sup>2</sup>
-Total surface area = <math>\pi r(l+r)</math>
+कुल पृष्ठीय क्षेत्रफल = <math>\pi r(l+r)</math>
 =<math>\frac{22}{7}\times 7 \times (10+7)=374</math> cm<sup>2</sup>