त्रिभुज के गुण: Difference between revisions

Latest revision as of 10:55, 18 September 2024

प्रमेय 1: समद्विबाहु त्रिभुज की समान भुजाओं के सम्मुख कोण समान होते हैं

चित्र 1- समद्विबाहु त्रिभुज

प्रमाण: चित्र 1 में दिखाए गए समद्विबाहु त्रिभुज $BCA$ पर विचार करें, जहाँ $AB=AC$ है।

हमें यह सिद्ध करना होगा कि भुजाओं $AB$ और $AC$ के सम्मुख कोण समान अर्थात् $\angle ABC=\angle ACB$ हैं।

हम पहले $\angle BAC$ का एक समद्विभाजक बनाते हैं और इसे $AD$ नाम देते हैं।

अब $\triangle BAD$ और $\triangle CAD$ में हमारे पास है,

$AB=AC$ (दिया हुआ)

$\angle BAD=\angle CAD$ (संरचना से)

$AD=AD$ (दोनों में समान)

अत:, $\triangle BAD\cong \triangle CAD$ (SAS सर्वांगसमता मानदंड द्वारा)

इसलिए, $\angle ABC=\angle ACB$ (CPCT द्वारा)

अतः सिद्ध हुआ।

प्रमेय 2: किसी त्रिभुज के समान कोणों की सम्मुख भुजाएँ समान होती हैं।

प्रमाण: चित्र-1 में दिखाए गए त्रिभुज $BCA$ में, आधार कोण समान हैं और हमें यह प्रमाणित करने की आवश्यकता है कि $AB=AC$ या

$BCA$ एक समद्विबाहु त्रिभुज है।

एक समद्विभाजक $AD$ की रचना कीजिए जो भुजा $BC$ से समकोण पर मिलता है।

अब $\triangle BAD$ और $\triangle CAD$ में हमारे पास है,

$\angle BAD=\angle CAD$ (संरचना से)

$AD=AD$ (समान भुजाएँ)

$\angle BDA=\angle CDA=90^{\circ }$ (संरचना से)

अत:, $\triangle BAD\cong \triangle CAD$ (ASA सर्वांगसमता मानदंड द्वारा)

इसलिए, $AB=AC$ (CPCT द्वारा)

अथवा $\triangle BCA$ समद्विबाहु है।

@@ Line 1: / Line 1: @@
-Theorem 1: Angles opposite to equal sides of an isosceles triangle are equal
+प्रमेय 1: समद्विबाहु त्रिभुज की समान भुजाओं के सम्मुख कोण समान होते हैं
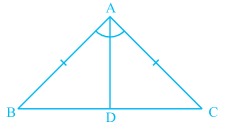
-[[File:Isosceles Triangle -1.jpg|alt=Fig 1 - Isosceles triangle|none|thumb|Fig 1 - Isosceles triangle]]
+[[File:Isosceles Triangle -1.jpg|alt=Fig 1 - Isosceles triangle|none|thumb|चित्र 1-  समद्विबाहु त्रिभुज]]
-Proof: Consider an isosceles triangle <math>BCA</math> shown in fig 1 where <math>AB=AC</math>.
+प्रमाण: चित्र 1 में दिखाए गए समद्विबाहु त्रिभुज <math>BCA</math> पर विचार करें, जहाँ <math>AB=AC</math> है।
-We need to prove that the angles opposite to the sides <math>AB</math> and <math>AC</math> are equal, that is, <math>\angle ABC = \angle ACB</math>
+हमें यह सिद्ध करना होगा कि भुजाओं <math>AB</math>और <math>AC</math> के सम्मुख कोण समान अर्थात् <math>\angle ABC = \angle ACB</math> हैं।
-We first draw a bisector of <math>\angle BAC</math> and name it as <math>AD</math>.
+हम पहले <math>\angle BAC</math>का एक समद्विभाजक बनाते हैं और इसे <math>AD</math> नाम देते हैं।
-Now in <math>\triangle BAD</math> and <math>\triangle CAD</math> we have,
+अब <math>\triangle BAD</math> और <math>\triangle CAD</math> में हमारे पास है,
-<math>AB=AC</math>                                                       (Given)
+<math>AB=AC</math>                                                       (दिया हुआ)
-<math>\angle BAD =\angle CAD </math>                                      (By construction)
+<math>\angle BAD =\angle CAD </math>                                      (संरचना से)
-<math>AD=AD</math>                                                           (Common to both)
+<math>AD=AD</math>                                                           (दोनों में समान)
-Thus,  <math>\triangle BAD \cong \triangle CAD</math>                            (By SAS congruence criterion)
+अत:,  <math>\triangle BAD \cong \triangle CAD</math>                            (SAS सर्वांगसमता मानदंड द्वारा)
-So, <math>\angle ABC =\angle ACB </math>                                    (By CPCT)
+इसलिए, <math>\angle ABC =\angle ACB </math>                                    (CPCT द्वारा)
-Hence proved.
+अतः सिद्ध हुआ।
-Theorem 2: The sides opposite to equal angles of a triangle are equal.
+प्रमेय 2: किसी त्रिभुज के समान कोणों की सम्मुख भुजाएँ समान होती हैं।
-Proof: In a triangle <math>BCA</math> shown in fig 1, base angles are equal and we need to prove that <math>AB=AC</math> or <math>BCA</math> is an isosceles triangle.
+प्रमाण: चित्र-1 में दिखाए गए त्रिभुज <math>BCA</math> में, आधार कोण समान हैं और हमें यह प्रमाणित करने की आवश्यकता है कि <math>AB=AC</math> या
-Construct a bisector <math>AD</math> which meets the side <math>BC</math> at right angles.
+<math>BCA</math> एक समद्विबाहु त्रिभुज है।
-Now in <math>\triangle BAD</math> and <math>\triangle CAD</math> we have,
+एक समद्विभाजक <math>AD</math> की रचना कीजिए जो भुजा <math>BC</math> से समकोण पर मिलता है।
-<math>\angle BAD =\angle CAD </math>                                        (By construction)
+अब  <math>\triangle BAD</math> और <math>\triangle CAD</math> में हमारे पास है,
-<math>AD=AD</math>                                                      (Common side)
+<math>\angle BAD =\angle CAD </math>                                         (संरचना से)
-<math>\angle BDA =\angle CDA = 90^\circ </math>                                (By construction)
+<math>AD=AD</math>                                                      (समान भुजाएँ)
-Thus, <math>\triangle BAD \cong \triangle CAD</math>                                   (By ASA congruence criterion)
+<math>\angle BDA =\angle CDA = 90^\circ </math>                               (संरचना से)
-So, <math>AB=AC</math>                                            (By CPCT)
+अत:, <math>\triangle BAD \cong \triangle CAD</math>                                 (ASA सर्वांगसमता मानदंड द्वारा)
-Or <math>\triangle BCA</math> is isosceles.
+इसलिए,  <math>AB=AC</math>                                            (CPCT द्वारा)
+अथवा <math>\triangle BCA</math> समद्विबाहु है।
 [[Category:त्रिभुज]][[Category:कक्षा-9]][[Category:गणित]]