कोण-कोण समरूपता कसौटी: Difference between revisions
No edit summary |
(added content) |
||
| Line 1: | Line 1: | ||
दो त्रिभुजों की समरूपता के लिए कोण-कोण (AA) कसौटी/मानदंड बताता है कि "यदि एक त्रिभुज के दो कोण क्रमशः दूसरे त्रिभुज के दो कोणों के समान हैं, तो दोनों त्रिभुज समरूप हैं"। | |||
AA कसौटी/मानदंड बताता है कि यदि एक त्रिभुज के दो कोण क्रमशः दूसरे त्रिभुज के दो कोणों के समान हैं, तो हम सिद्ध कर सकते हैं कि दोनों त्रिभुजों पर तीसरा कोण भी समान होगा। यह त्रिभुज के कोण योग गुण की मदद से किया जा सकता है। | |||
== | == उदाहरण == | ||
1. | 1.विकर्णों <math>AC</math> और <math>BD</math> एक समलंब <math>ABCD</math>,जिसमें <math>AB \parallel DC</math> हो और एक दूसरे को बिंदु <math>O</math> पर प्रतिच्छेद करते हैं। दो त्रिभुजों के लिए समरूपता मानदंड का उपयोग करते हुए दर्शाइए कि <math>\frac{OA}{OC}=\frac{OB}{OD}</math> | ||
''' | '''हल:''' | ||
आइए एक समलंब <math>ABCD</math> चतुर्भुज बनाते हैं जिसमें <math>AB \parallel DC</math> हो | |||
[[File:Example-4.jpg|none|thumb]] | [[File:Example-4.jpg|none|thumb]] | ||
यदि एक त्रिभुज के दो कोण क्रमशः दूसरे त्रिभुज के दो कोणों के समान हों, तो दोनों त्रिभुज समरूप होते हैं। | |||
इसे दो त्रिभुजों के लिए AA समरूपता मानदंड के रूप में जाना जाता है। | |||
In <math>\triangle AOB</math> and <math>\triangle COD</math> | In <math>\triangle AOB</math> and <math>\triangle COD</math> | ||
<math>\angle AOB =\angle COD</math> ( | <math>\angle AOB =\angle COD</math> (ऊर्ध्वाधर विपरीत कोण) | ||
<math>\angle BAO =\angle DCO</math> ( | <math>\angle BAO =\angle DCO</math> (वैकल्पिक आंतरिक कोण) | ||
अत: <math>\triangle AOB \sim \triangle COD</math> (AA समरूपता कसौटी) | |||
अत: <math>\frac{OA}{OC}=\frac{OB}{OD}</math> | |||
[[Category:त्रिभुज]][[Category:गणित]][[Category:कक्षा-10]] | [[Category:त्रिभुज]][[Category:गणित]][[Category:कक्षा-10]] | ||
Latest revision as of 17:09, 23 September 2024
दो त्रिभुजों की समरूपता के लिए कोण-कोण (AA) कसौटी/मानदंड बताता है कि "यदि एक त्रिभुज के दो कोण क्रमशः दूसरे त्रिभुज के दो कोणों के समान हैं, तो दोनों त्रिभुज समरूप हैं"।
AA कसौटी/मानदंड बताता है कि यदि एक त्रिभुज के दो कोण क्रमशः दूसरे त्रिभुज के दो कोणों के समान हैं, तो हम सिद्ध कर सकते हैं कि दोनों त्रिभुजों पर तीसरा कोण भी समान होगा। यह त्रिभुज के कोण योग गुण की मदद से किया जा सकता है।
उदाहरण
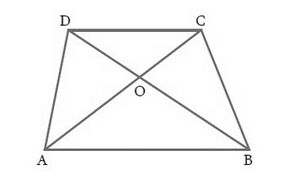
1.विकर्णों और एक समलंब ,जिसमें हो और एक दूसरे को बिंदु पर प्रतिच्छेद करते हैं। दो त्रिभुजों के लिए समरूपता मानदंड का उपयोग करते हुए दर्शाइए कि
हल:
आइए एक समलंब चतुर्भुज बनाते हैं जिसमें हो
यदि एक त्रिभुज के दो कोण क्रमशः दूसरे त्रिभुज के दो कोणों के समान हों, तो दोनों त्रिभुज समरूप होते हैं।
इसे दो त्रिभुजों के लिए AA समरूपता मानदंड के रूप में जाना जाता है।
In and
(ऊर्ध्वाधर विपरीत कोण)
(वैकल्पिक आंतरिक कोण)
अत: (AA समरूपता कसौटी)
अत: