रेखा: Difference between revisions
Ramamurthy (talk | contribs) |
(added internal links) |
||
| Line 8: | Line 8: | ||
# '''ऊंचाई''': एक रेखा जो एक शीर्ष और विपरीत दिशा से होकर गुजरती है, और उस तरफ से समकोण बनाती है। | # '''ऊंचाई''': एक रेखा जो एक शीर्ष और विपरीत दिशा से होकर गुजरती है, और उस तरफ से समकोण बनाती है। | ||
# '''माध्यिका''': एक रेखा जो एक भुजा के मध्यबिंदु और विपरीत शीर्ष से होकर गुजरती है। | # '''माध्यिका''': एक रेखा जो एक भुजा के मध्यबिंदु और विपरीत शीर्ष से होकर गुजरती है। | ||
# '''लंब समद्विभाजक''': एक रेखा जो त्रिभुज की एक भुजा को उसके मध्य बिंदु पर काटती है और भुजा के साथ समकोण बनाती है। | # '''लंब समद्विभाजक''': एक रेखा जो त्रिभुज की एक भुजा को उसके [[मध्य-बिंदु प्रमेय|मध्य बिंदु]] पर काटती है और भुजा के साथ समकोण बनाती है। | ||
# '''आंतरिक/आंतरिक कोण समद्विभाजक''': एक रेखा जो त्रिभुज के आंतरिक कोण को दो सर्वांगसम भागों में विभाजित करती है। | # '''आंतरिक/आंतरिक कोण समद्विभाजक''': एक रेखा जो त्रिभुज के आंतरिक कोण को दो सर्वांगसम भागों में विभाजित करती है। | ||
# '''बाहरी/बाह्य कोण समद्विभाजक''': एक रेखा जो त्रिभुज के बाहरी कोण को दो सर्वांगसम भागों में विभाजित करती है। | # '''बाहरी/बाह्य कोण समद्विभाजक''': एक रेखा जो त्रिभुज के बाहरी कोण को दो सर्वांगसम भागों में विभाजित करती है। | ||
== स्पष्टीकरण == | == स्पष्टीकरण == | ||
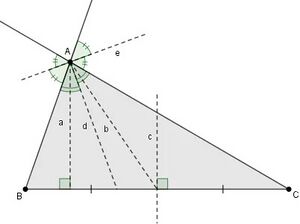
चूँकि एक त्रिभुज की तीन भुजाएँ और शीर्ष होते हैं, इसलिए इसमें तीन ऊँचाई, माध्यिकाएँ, लम्ब समद्विभाजक, आंतरिक कोण समद्विभाजक और बाह्य कोण समद्विभाजक भी होते हैं। उदाहरण के लिए, △ABC के शीर्ष A के अनुरूप ऊँचाई, माध्यिका, लंब समद्विभाजक, आंतरिक कोण समद्विभाजक और बाह्य कोण समद्विभाजक को क्रमशः <math>a, b, c, d,e</math> के रूप में दिखाया गया है। अक्सर हम आंतरिक कोण समद्विभाजक को मात्र एक आंतरिक कोण समद्विभाजक कहते हैं। इस पर बल दिए बिना कोण समद्विभाजक एक आंतरिक कोण के लिए है। | चूँकि एक त्रिभुज की तीन भुजाएँ और शीर्ष होते हैं, इसलिए इसमें तीन ऊँचाई, माध्यिकाएँ, लम्ब समद्विभाजक, आंतरिक कोण समद्विभाजक और बाह्य [[कोण]] समद्विभाजक भी होते हैं। उदाहरण के लिए, △ABC के शीर्ष A के अनुरूप ऊँचाई, माध्यिका, लंब समद्विभाजक, आंतरिक कोण समद्विभाजक और बाह्य कोण समद्विभाजक को क्रमशः <math>a, b, c, d,e</math> के रूप में दिखाया गया है। अक्सर हम आंतरिक कोण समद्विभाजक को मात्र एक आंतरिक कोण समद्विभाजक कहते हैं। इस पर बल दिए बिना कोण समद्विभाजक एक आंतरिक कोण के लिए है। | ||
इन सभी विशेष रेखाओं को सेवियन भी कहा जाता है, जिनका नाम एक इतालवी गणितज्ञ जियोवानी सेवा के नाम पर रखा गया है। सरल शब्दों में सेवियन एक ऐसी रेखा है जो त्रिभुज के शीर्ष और उस शीर्ष के विपरीत भुजा दोनों को काटती है। | इन सभी विशेष रेखाओं को सेवियन भी कहा जाता है, जिनका नाम एक इतालवी गणितज्ञ जियोवानी सेवा के नाम पर रखा गया है। सरल शब्दों में सेवियन एक ऐसी रेखा है जो त्रिभुज के शीर्ष और उस शीर्ष के विपरीत भुजा दोनों को काटती है। | ||
Latest revision as of 09:17, 5 November 2024
रेखा एक सीधी एक-आयामी आकृति है जिसमें कोई मोटाई नहीं होती है, और यह दोनों दिशाओं में अंतहीन रूप से फैली हुई होती है।
रेखाओं के प्रकार
- ऊंचाई: एक रेखा जो एक शीर्ष और विपरीत दिशा से होकर गुजरती है, और उस तरफ से समकोण बनाती है।
- माध्यिका: एक रेखा जो एक भुजा के मध्यबिंदु और विपरीत शीर्ष से होकर गुजरती है।
- लंब समद्विभाजक: एक रेखा जो त्रिभुज की एक भुजा को उसके मध्य बिंदु पर काटती है और भुजा के साथ समकोण बनाती है।
- आंतरिक/आंतरिक कोण समद्विभाजक: एक रेखा जो त्रिभुज के आंतरिक कोण को दो सर्वांगसम भागों में विभाजित करती है।
- बाहरी/बाह्य कोण समद्विभाजक: एक रेखा जो त्रिभुज के बाहरी कोण को दो सर्वांगसम भागों में विभाजित करती है।
स्पष्टीकरण
चूँकि एक त्रिभुज की तीन भुजाएँ और शीर्ष होते हैं, इसलिए इसमें तीन ऊँचाई, माध्यिकाएँ, लम्ब समद्विभाजक, आंतरिक कोण समद्विभाजक और बाह्य कोण समद्विभाजक भी होते हैं। उदाहरण के लिए, △ABC के शीर्ष A के अनुरूप ऊँचाई, माध्यिका, लंब समद्विभाजक, आंतरिक कोण समद्विभाजक और बाह्य कोण समद्विभाजक को क्रमशः के रूप में दिखाया गया है। अक्सर हम आंतरिक कोण समद्विभाजक को मात्र एक आंतरिक कोण समद्विभाजक कहते हैं। इस पर बल दिए बिना कोण समद्विभाजक एक आंतरिक कोण के लिए है।
इन सभी विशेष रेखाओं को सेवियन भी कहा जाता है, जिनका नाम एक इतालवी गणितज्ञ जियोवानी सेवा के नाम पर रखा गया है। सरल शब्दों में सेवियन एक ऐसी रेखा है जो त्रिभुज के शीर्ष और उस शीर्ष के विपरीत भुजा दोनों को काटती है।